Teori Jaringan - Resonansi Paralel
Pada bab sebelumnya, kita telah membahas pentingnya resonansi deret. Sekarang, mari kita bahas resonansi paralel di sirkuit RLC.
Diagram Sirkuit Resonansi Paralel
Jika resonansi terjadi pada rangkaian RLC paralel, maka disebut sebagai Parallel Resonance. Simak berikut iniparallel RLC circuit, yang direpresentasikan dalam domain fasor.
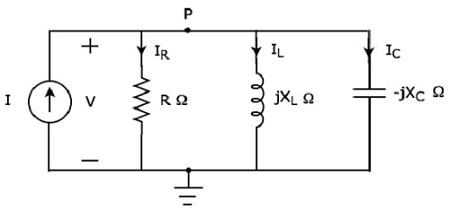
Di sini, elemen pasif seperti resistor, induktor dan kapasitor dihubungkan secara paralel. Seluruh kombinasi ini masukparallel dengan masukan sumber arus sinusoidal.
Menulis nodal equation di node P.
$$ - I + I_R + I_L + I_C = 0 $$
$$ \ Rightarrow - I + \ frac {V} {R} + \ frac {V} {j X_L} + \ frac {V} {- j X_C} = 0 $$
$$ \ Rightarrow I = \ frac {V} {R} - \ frac {jV} {X_L} + \ frac {jV} {X_C} $$
$ \ Rightarrow I = V [\ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup] $Equation 1
Persamaan di atas berbentuk I = VY.
Oleh karena itu, admittance Y dari rangkaian RLC paralel akan
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup $$
Parameter & Kuantitas Listrik pada Resonansi
Sekarang, mari kita turunkan nilai parameter dan besaran listrik pada resonansi rangkaian RLC paralel satu per satu.
Frekuensi resonansi
Kami tahu bahwa resonant frequency, fradalah frekuensi terjadinya resonansi. Dalam rangkaian RLC paralel resonansi terjadi, ketika istilah imajiner admitansi, Y adalah nol. yaitu, nilai $ \ frac {1} {X_C} - \ frac {1} {X_L} $ harus sama dengan nol
$$ \ Rightarrow \ frac {1} {X_C} = \ frac {1} {X_L} $$
$$ \ Rightarrow X_L = X_C $$
Kondisi resonansi di atas sama dengan rangkaian RLC seri. Sehinggaresonant frequency, fr akan sama di kedua rangkaian RLC seri dan rangkaian RLC paralel.
Oleh karena itu, resonant frequency, fr dari rangkaian RLC paralel adalah
$$ f_r = \ frac {1} {2 \ pi \ sqrt {LC}} $$
Dimana,
- L adalah induktansi induktor.
- C adalah kapasitansi kapasitor.
Itu resonant frequency, fr Rangkaian RLC paralel hanya bergantung pada induktansi L dan kapasitansi C. Tapi, itu tidak tergantung pada perlawananR.
Masuk
Kami mendapatkan admittance Y rangkaian RLC paralel sebagai
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup $$
Gantikan, $ X_L = X_C $ dalam persamaan di atas.
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_C} \ rgroup $$
$$ \ Rightarrow Y = \ frac {1} {R} + j (0) $$
$$ \ Rightarrow Y = \ frac {1} {R} $$
Pada resonansi, admittance, Y dari rangkaian RLC paralel sama dengan kebalikan dari resistansi, R. yaitu, $ \ mathbf {\ mathit {Y = \ frac {1} {R}}} $
Tegangan di setiap Elemen
Pengganti, $ \ frac {1} {X_C} - \ frac {1} {X_L} = 0 $ pada Persamaan 1
$$ I = V [\ frac {1} {R} + j (0)] $$
$$ \ Rightarrow I = \ frac {V} {R} $$
$$ \ Rightarrow V = IR $$
Oleh karena itu, voltage di semua elemen rangkaian RLC paralel pada resonansi V = IR.
Pada resonansi, penerimaan rangkaian RLC paralel mencapai nilai minimum. Karenanya,maximum voltage hadir di setiap elemen rangkaian ini pada resonansi.
Arus mengalir melalui Resistor
Arus yang mengalir melalui resistor adalah
$$ I_R = \ frac {V} {R} $$
Gantikan nilai V dalam persamaan di atas.
$$ I_R = \ frac {IR} {R} $$
$$ \ Rightarrow I_R = I $$
Oleh karena itu, current flowing through resistor beresonansi adalah $ \ mathbf {\ mathit {I_R = I}} $.
Arus mengalir melalui Induktor
Arus yang mengalir melalui induktor adalah
$$ I_L = \ frac {V} {j X_L} $$
Gantikan nilai V dalam persamaan di atas.
$$ I_L = \ frac {IR} {j X_L} $$
$$ \ Rightarrow I_L = -j \ lgroup \ frac {R} {X_L} \ rgroup I $$
$$ \ Rightarrow I_L = -jQI $$
Oleh karena itu, current flowing through inductor beresonansi adalah $ I_L = -jQI $.
Sehingga magnitude arus yang mengalir melalui induktor pada resonansi akan
$$ | I_L | = QI $$
Dimana, Q adalah Quality factor dan nilainya sama dengan $ \ frac {R} {X_L} $
Arus mengalir melalui Kapasitor
Arus yang mengalir melalui kapasitor adalah
$$ I_C = \ frac {V} {- j X_C} $$
Gantikan nilai V dalam persamaan di atas.
$$ I_C = \ frac {IR} {- j X_C} $$
$$ \ Rightarrow I_C = j \ lgroup \ frac {R} {X_C} \ rgroup I $$
$$ \ Rightarrow I_C = jQI $$
Oleh karena itu, current flowing through capacitor pada resonansi adalah $ I_C = jQI $
Sehingga magnitude arus yang mengalir melalui kapasitor pada resonansi akan
$$ | I_C | = QI $$
Dimana, Q adalah Quality factor dan nilainya sama dengan $ \ frac {R} {X_C} $
Note - Rangkaian RLC resonansi paralel disebut sebagai current magnificationsirkuit. Sebab, besarnya arus yang mengalir melalui induktor dan kapasitor adalah sama dengan Q kali input sinusoidal saat saya .