Teori Jaringan - Sirkuit Ekuivalen
Jika rangkaian terdiri dari dua atau lebih elemen pasif serupa dan terhubung secara eksklusif dari tipe seri atau tipe paralel, maka kita dapat menggantinya dengan satu elemen pasif ekuivalen. Karenanya, sirkuit ini disebut sebagaiequivalent circuit.
Dalam bab ini, mari kita bahas tentang dua rangkaian ekivalen berikut.
- Rangkaian Setara Seri
- Rangkaian Ekuivalen Paralel
Rangkaian Setara Seri
Jika elemen pasif serupa dihubungkan series, maka arus yang sama akan mengalir melalui semua elemen ini. Tapi, tegangan dibagi di setiap elemen.
Simak berikut ini circuit diagram.
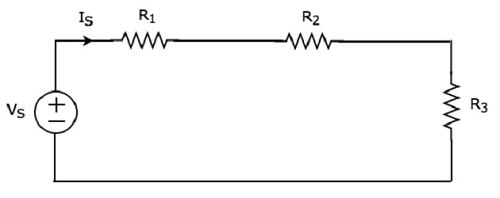
Ini memiliki sumber tegangan tunggal (V S ) dan tiga resistor yang memiliki resistansi R 1 , R 2 dan R 3 . Semua elemen ini dihubungkan secara seri. Arus IS mengalir melalui semua elemen ini.
Sirkuit di atas hanya memiliki satu mesh. ItuKVL equation sekitar jala ini
$$ V_S = V_1 + V_2 + V_3 $$
Gantikan $ V_1 = I_S R_1, \: V_2 = I_S R_2 $ dan $ V_3 = I_S R_3 $ dalam persamaan di atas.
$$ V_S = I_S R_1 + I_S R_2 + I_S R_3 $$
$$ \ Rightarrow V_S = I_S (R_1 + R_2 + R_3) $$
Persamaan di atas berupa $ V_S = I_S R_ {Persamaan} $ dimana,
$$ R_ {Persamaan} = R_1 + R_2 + R_3 $$
Itu equivalent circuit diagram dari rangkaian yang diberikan ditunjukkan pada gambar berikut.
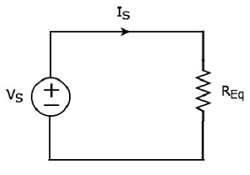
Artinya, jika beberapa resistor dihubungkan secara seri, maka kita dapat menggantinya dengan equivalent resistor. Hambatan dari resistor ekivalen ini sama dengan jumlah resistansi dari semua resistor ganda tersebut.
Note 1- Jika induktor 'N' yang memiliki induktansi L 1 , L 2 , ..., L N dirangkai seri, makaequivalent inductance akan
$$ L_ {Persamaan} = L_1 + L_2 + ... + L_N $$
Note 2- Jika kapasitor 'N' yang memiliki kapasitansi C 1 , C 2 , ..., C N dirangkai seri, makaequivalent capacitance akan
$$ \ frac {1} {C_ {Persamaan}} = \ frac {1} {C_1} + \ frac {1} {C_2} + ... + \ frac {1} {C_N} $$
Rangkaian Ekuivalen Paralel
Jika elemen pasif serupa dihubungkan parallel, maka tegangan yang sama akan dipertahankan di setiap elemen. Tapi, arus yang mengalir melalui setiap elemen terbagi.
Simak berikut ini circuit diagram.

Ini memiliki sumber arus tunggal (I S ) dan tiga resistor yang memiliki resistansi R 1 , R 2 , dan R 3 . Semua elemen ini terhubung secara paralel. Tegangan (V S ) tersedia di semua elemen ini.
Sirkuit di atas hanya memiliki satu node utama (P) kecuali node Ground. ItuKCL equation pada simpul utama ini (P) adalah
$$ I_S = I_1 + I_2 + I_3 $$
Gantikan $ I_1 = \ frac {V_S} {R_1}, \: I_2 = \ frac {V_S} {R_2} $ dan $ I_3 = \ frac {V_S} {R_3} $ dalam persamaan di atas.
$$ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} + \ frac {V_S} {R_3} $$
$$ \ Rightarrow I_S = V_S \ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup $$
$$ \ Rightarrow V_S = I_S \ left [\ frac {1} {\ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup} \ right] $$
Persamaan di atas berupa V S = I S R Persamaan dimana,
$$ R_ {Persamaan} = \ frac {1} {\ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup} $$
$$ \ frac {1} {R_ {Persamaan}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} $$
Itu equivalent circuit diagram dari rangkaian yang diberikan ditunjukkan pada gambar berikut.
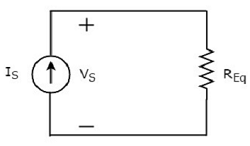
Artinya, jika beberapa resistor dihubungkan secara paralel, maka kita dapat menggantinya dengan resistor yang setara. Resistensi iniequivalent resistor sama dengan kebalikan dari jumlah kebalikan dari masing-masing resistansi dari semua resistor ganda tersebut.
Note 1- Jika induktor 'N' yang memiliki induktansi L 1 , L 2 , ..., L N dihubungkan paralel, makaequivalent inductance akan
$$ \ frac {1} {L_ {Persamaan}} = \ frac {1} {L_1} + \ frac {1} {L_2} + ... + \ frac {1} {L_N} $$
Note 2- Jika kapasitor 'N' yang memiliki kapasitansi C 1 , C 2 , ..., C N dihubungkan paralel, makaequivalent capacitance akan
$$ C_ {Persamaan} = C_1 + C_2 + ... + C_N $$