Teori Jaringan - Hukum Kirchhoff
Elemen jaringan dapat berupa salah satu dari active atau passiveTipe. Setiap rangkaian atau jaringan listrik berisi salah satu dari dua jenis elemen jaringan ini atau kombinasi keduanya.
Sekarang, mari kita bahas tentang dua undang-undang berikut, yang lebih dikenal sebagai Kirchhoff’s laws.
- Hukum Kirchhoff Saat Ini
- Hukum Tegangan Kirchhoff
Hukum Kirchhoff Saat Ini
Hukum Arus Kirchhoff (KCL) menyatakan bahwa jumlah aljabar arus yang meninggalkan (atau memasuki) sebuah simpul sama dengan nol.
SEBUAH Nodeadalah titik di mana dua atau lebih elemen rangkaian terhubung dengannya. Jika hanya dua elemen rangkaian yang dihubungkan ke sebuah node, maka dikatakan node sederhana. Jika tiga atau lebih elemen sirkuit dihubungkan ke sebuah node, maka disebut nodePrincipal Node.
Mathematically, KCL dapat direpresentasikan sebagai
$$ \ displaystyle \ sum \ limit_ {m = 1} ^ M I_m = 0 $$
Dimana,
Imadalah arus cabang ke- m yang meninggalkan node.
M adalah jumlah cabang yang terhubung ke sebuah node.
Pernyataan di atas dari KCLjuga dapat dinyatakan sebagai "jumlah aljabar arus yang memasuki suatu node sama dengan jumlah aljabar arus yang meninggalkan node". Mari kita verifikasi pernyataan ini melalui contoh berikut.
Contoh
Menulis KCL equation di node P dari gambar berikut.
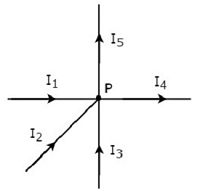
Pada gambar di atas, arus cabang I 1 , I 2 dan I 3 adalahentering di simpul P. Jadi, pertimbangkan tanda negatif untuk ketiga arus ini.
Pada gambar di atas, arus cabang I 4 dan I 5 adalahleaving dari simpul P. Jadi, pertimbangkan tanda positif untuk kedua arus ini.
Itu KCL equation di node P akan
$$ - I_1 - I_2 - I_3 + I_4 + I_5 = 0 $$
$$ \ Rightarrow I_1 + I_2 + I_3 = I_4 + I_5 $$
Dalam persamaan di atas, sisi kiri mewakili jumlah arus yang masuk, sedangkan sisi kanan mewakili jumlah arus yang keluar.
Dalam tutorial ini, kita akan mempertimbangkan tanda positif ketika arus meninggalkan simpul dan tanda negatif ketika memasuki simpul. Demikian pula, Anda dapat mempertimbangkan tanda negatif ketika arus meninggalkan simpul dan tanda positif ketika memasuki simpul. Dalam kedua kasus, fileresult will be same.
Note - KCL tidak bergantung pada sifat elemen jaringan yang terhubung ke node.
Hukum Tegangan Kirchhoff
Hukum Tegangan Kirchhoff (KVL) menyatakan bahwa jumlah aljabar tegangan di sekitar loop atau mesh sama dengan nol.
SEBUAH Loopadalah jalur yang berakhir di simpul yang sama tempat asalnya. Sebaliknya, aMesh adalah loop yang tidak berisi loop lain di dalamnya.
Secara matematis, KVL dapat direpresentasikan sebagai
$$ \ displaystyle \ sum \ batas_ {n = 1} ^ N V_n = 0 $$
Dimana,
Vnadalah tegangan elemen ke n dalam satu loop (mesh).
N adalah jumlah elemen jaringan dalam loop (mesh).
Pernyataan di atas dari KVLjuga dapat dinyatakan sebagai "jumlah aljabar sumber tegangan sama dengan jumlah aljabar penurunan tegangan yang ada dalam satu lingkaran". Mari kita verifikasi pernyataan ini dengan bantuan contoh berikut.
Contoh
Menulis KVL equation di sekitar loop dari sirkuit berikut.
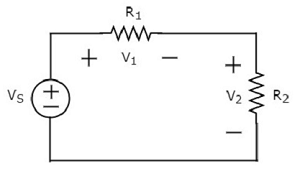
Diagram rangkaian di atas terdiri dari sumber tegangan, V S secara seri dengan dua resistor R 1 dan R 2 . Tegangan turun di resistor R 1 dan R 2 adalah V 1 dan V 2 masing-masing.
Menerapkan KVL di sekitar lingkaran.
$$ V_S - V_1 - V_2 = 0 $$
$$ \ Rightarrow V_S = V_1 + V_2 $$
Dalam persamaan di atas, istilah sisi kiri mewakili sumber tegangan tunggal VS. Sedangkan sisi kanan mewakilisum of voltage drops. Dalam contoh ini, kami hanya mempertimbangkan satu sumber tegangan. Itu sebabnya ruas kiri hanya berisi satu suku. Jika kita menganggap beberapa sumber tegangan, maka sisi kiri berisi jumlah sumber tegangan.
Dalam tutorial ini, kami mempertimbangkan tanda tegangan setiap elemen sebagai polaritas terminal kedua yang ada saat melakukan perjalanan di sekitar loop. Demikian pula, Anda dapat mempertimbangkan tanda setiap tegangan sebagai polaritas terminal pertama yang ada saat melakukan perjalanan di sekitar loop. Dalam kedua kasus, fileresult will be same.
Note - KVL tidak bergantung pada sifat elemen jaringan yang ada dalam satu loop.