DSP-信号畳み込みの操作
時間領域での2つの信号の畳み込みは、周波数領域でのそれらの表現の乗算に相当します。数学的には、2つの信号の畳み込みを次のように書くことができます。
$$ y(t)= x_ {1}(t)* x_ {2}(t)$$ $$ = \ int _ {-\ infty} ^ {\ infty} x_ {1}(p).x_ {2 }(tp)dp $$畳み込みの手順
- 信号Xテイク1(t)をとt = PそれはXがあることを置く1(p)を。
- 信号Xテイク2(t)を、ステップ1を行うと、それは、X作る2(p)を。
- 信号を折りたたむ、つまりx 2(-p)にします。
- 上記信号xからシフト時間行う2 [ - (PT)]を
- 次に、両方の信号の乗算を行います。つまり、$ x_ {1}(p).x_ {2} [−(p−t)] $
例
ステップ信号u(t)を独自の種類で畳み込みます。
$ y(t)= u(t)* u(t)$
$ = \ int _ {-\ infty} ^ {\ infty} [u(p).u [-(pt)] dp $
これで、このtはゼロより大きくても小さくてもかまいません。これを下の図に示します。
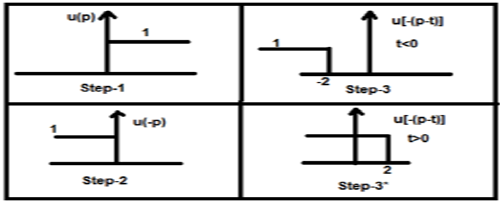
したがって、上記の場合、結果は次の可能性で発生します
$ y(t)= \ begin {cases} 0、&if \ quad t <0 \\\ int_ {0} ^ {t} 1dt、&for \ quad t> 0 \ end {cases} $
$ = \ begin {cases} 0、&if \ quad t <0 \\ t、&t> 0 \ end {cases} = r(t)$
畳み込みのプロパティ
可換
畳み込みの順序は重要ではないと述べています。これは数学的に次のように示すことができます。
$$ x_ {1}(t)* x_ {2}(t)= x_ {2}(t)* x_ {1}(t)$$連想
それは、3つの信号を含む畳み込みの順序は何でもよいと述べています。数学的には、次のように表示できます。
$$ x_ {1}(t)* [x_ {2}(t)* x_ {3}(t)] = [x_ {1}(t)* x_ {2}(t)] * x_ {3} (t)$$分配法則
最初に2つの信号を追加してから、3番目の信号に畳み込みを行うことができます。これは、2つの信号を個別に3番目の信号で畳み込み、最後に追加することと同じです。数学的には、これは次のように書くことができます。
$$ x_ {1}(t)* [x_ {2}(t)+ x_ {3}(t)] = [x_ {1}(t)* x_ {2}(t)+ x_ {1}( t)* x_ {3}(t)] $$範囲
信号が2つの信号の畳み込みの結果である場合、信号の面積はそれらの個々の信号の乗算です。数学的にこれは書くことができます
もし$ Y(T)= X_ {1} * X_ {2}(t)は$
次に、y(t)の面積= x 1の面積(t)X x 2の面積(t)
スケーリング
2つの信号が未知の定数「a」にスケーリングされ、畳み込みが行われると、結果の信号も同じ定数「a」に畳み込まれ、以下に示すようにその量で除算されます。
の場合、$ x_ {1}(t)* x_ {2}(t)= y(t)$
次に、$ x_ {1}(at)* x_ {2}(at)= \ frac {y(at)} {a}、\ ne 0 $
ディレイ
信号y(t)が2つの信号x1(t)とx2(t)の畳み込みの結果であると仮定します。2つの信号がそれぞれ時間t1とt2だけ遅延した場合、結果の信号y(t)は(t1 + t2)だけ遅延します。数学的には、次のように書くことができます。
の場合、$ x_ {1}(t)* x_ {2}(t)= y(t)$
次に、$ x_ {1}(t-t_ {1})* x_ {2}(t-t_ {2})= y [t-(t_ {1} + t_ {2})] $
解決された例
Example 1 −信号u(t-1)とu(t-2)の畳み込みを見つけます。
Solution−与えられた信号はu(t-1)とu(t-2)です。それらの畳み込みは、以下に示すように実行できます。
$ y(t)= u(t-1)* u(t-2)$
$ y(t)= \ int _ {-\ infty} ^ {+ \ infty} [u(t-1).u(t-2)] dt $
$ = r(t-1)+ r(t-2)$
$ = r(t-3)$
Example 2 −によって与えられる2つの信号の畳み込みを見つけます
$x_{1}(n) = \lbrace 3,-2, 2\rbrace $
$ x_ {2}(n)= \ begin {cases} 2、&0 \ leq n \ leq 4 \\ 0、&x>他の場所\ end {cases} $
Solution −
x 2(n)は、$ x_ {2}(n)= \ lbrace 2,2,2,2,2 \ rbrace Originalfirst $としてデコードできます。
x 1(n)は以前に$ = \ lbrace 3、-2,3 \ rbrace = 3-2Z ^ {-1} + 2Z ^ {-2} $が与えられています
同様に、$ x_ {2}(z)= 2 + 2Z ^ {-1} + 2Z ^ {-2} + 2Z ^ {-3} + 2Z ^ {-4} $
結果の信号、
$ X(Z)= X_ {1}(Z)X_ {2}(z)$
$ = \ lbrace 3-2Z ^ {-1} + 2Z ^ {-2} \ rbrace \ times \ lbrace 2 + 2Z ^ {-1} + 2Z ^ {-2} + 2Z ^ {-3} + 2Z ^ {-4} \ rbrace $
$ = 6 + 2Z ^ {-1} + 6Z ^ {-2} + 6Z ^ {-3} + 6Z ^ {-4} + 6Z ^ {-5} $
上記の逆Z変換を行うと、結果の信号は次のようになります。
$ x(n)= \ lbrace 6,2,6,6,6,0,4 \ rbrace $最初の原点
Example 3 −次の2つの信号の畳み込みを決定します−
$x(n) = \lbrace 2,1,0,1\rbrace$
$h(n) = \lbrace 1,2,3,1\rbrace$
Solution −
信号のZ変換を行うと、次のようになります。
$ x(z)= 2 + 2Z ^ {-1} + 2Z ^ {-3} $
そして$ h(n)= 1 + 2Z ^ {-1} + 3Z ^ {-2} + Z ^ {-3} $
ここで、2つの信号の畳み込みは、それらのZ変換の乗算を意味します
つまり、$ Y(Z)= X(Z)\ times h(Z)$
$ = \ lbrace 2 + 2Z ^ {-1} + 2Z ^ {-3} \ rbrace \ times \ lbrace 1 + 2Z ^ {-1} + 3Z ^ {-2} + Z ^ {-3} \ rbrace $
$ = \ lbrace 2 + 5Z ^ {-1} + 8Z ^ {-2} + 6Z ^ {-3} + 3Z ^ {-4} + 3Z ^ {-5} + Z ^ {-6} \ rbrace $
逆Z変換を行うと、結果の信号は次のように記述できます。
$ y(n)= \ lbrace 2,5,8,6,6,1 \ rbrace Originalfirst $