DSP-Z変換プロパティ
この章では、Z変換の基本的な特性を理解します。
直線性
2つ以上の個別の離散信号に定数を掛けると、それぞれのZ変換にも同じ定数が掛けられると記載されています。
数学的には、
$$ a_1x_1(n)+ a_2x_2(n)= a_1X_1(z)+ a_2X_2(z)$$Proof −私たちはそれを知っています、
$$ X(Z)= \ sum_ {n =-\ infty} ^ \ infty x(n)Z ^ {-n} $$$ = \ sum_ {n =-\ infty} ^ \ infty(a_1x_1(n)+ a_2x_2(n))Z ^ {-n} $
$ = a_1 \ sum_ {n =-\ infty} ^ \ infty x_1(n)Z ^ {-n} + a_2 \ sum_ {n =-\ infty} ^ \ infty x_2(n)Z ^ {-n} $
$ = a_1X_1(z)+ a_2X_2(z)$ (したがって証明済み)
ここで、ROCは$ ROC_1 \ bigcap ROC_2 $です。
タイムシフト
タイムシフトプロパティは、離散信号の時間領域の変化がZ領域にどのように影響するかを示します。これは次のように記述できます。
$$ x(n-n_0)\ longleftrightarrow X(Z)Z ^ {-n} $$または$ x(n-1)\ longleftrightarrow Z ^ {-1} X(Z)$
Proof −
してみましょう$ Y(P)= X(PK)$
$ Y(z)= \ sum_ {p =-\ infty} ^ \ infty y(p)Z ^ {-p} $
$ = \ sum_ {p =-\ infty} ^ \ infty(x(pk))Z ^ {-p} $
s = pkとします
$ = \ sum_ {s =-\ infty} ^ \ infty x(s)Z ^ {-(s + k)} $
$ = \ sum_ {s =-\ infty} ^ \ infty x(s)Z ^ {-s} Z ^ {-k} $
$ = Z ^ {-k} [\ sum_ {s =-\ infty} ^ \ infty x(m)Z ^ {-s}] $
$ = Z ^ {-k} X(Z)$ (したがって証明済み)
ここで、ROCはZ = 0(p> 0)またはZ =∞(p <0)と書くことができます。
例
U(n)とU(n-1)は次のようにプロットできます
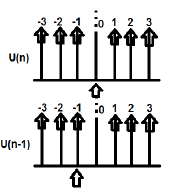
U(n)cabのZ変換は次のように記述されます。
$ \ sum_ {n =-\ infty} ^ \ infty [U(n)] Z ^ {-n} = 1 $
U(n-1)のZ変換は次のように書くことができます。
$ \ sum_ {n =-\ infty} ^ \ infty [U(n-1)] Z ^ {-n} = Z ^ {-1} $
したがって、ここで$ x(n-n_0)= Z ^ {-n_0} X(Z)$ (したがって証明済み)
タイムスケーリング
Time Scalingプロパティは、時間を離散形式でスケーリングしたときに信号のZドメインがどうなるかを示します。これは次のように記述できます。
$$ a ^ nx(n)\ longleftrightarrow X(a ^ {-1} Z)$$Proof −
ましょう$ Y(P)= A ^ {P} X(P)$を
$ Y(P)= \ sum_ {p =-\ infty} ^ \ infty y(p)Z ^ {-p} $
$ = \ sum_ {p =-\ infty} ^ \ infty a ^ px(p)Z ^ {-p} $
$ = \ sum_ {p =-\ infty} ^ \ infty x(p)[a ^ {-1} Z] ^ {-p} $
$ = X(a ^ {-1} Z)$ (したがって証明済み)
ROC:= Mod(ar1)<Mod(Z)<Mod(ar2)ここで、Mod = Modulus
例
時間スケーリングプロパティを使用して、$ x(n)= a ^ n \ cos \ omega n $のZ変換を決定しましょう。
Solution −
信号$ \ cos(\ omega n)$のZ変換が−で与えられることはすでに知っています。
$$ \ sum_ {n =-\ infty} ^ \ infty(\ cos \ omega n)Z ^ {-n} =(Z ^ 2-Z \ cos \ omega)/(Z ^ 2-2Z \ cos \ omega +1)$$
ここで、時間スケーリングプロパティを適用すると、$ a ^ n \ cos \ omega n $のZ変換は次のように記述できます。
$ \ sum_ {n =-\ infty} ^ \ infty(a ^ n \ cos \ omega n)Z ^ {-n} = X(a ^ {-1} Z)$
$ = [(a ^ {-1} Z)^ 2-(a ^ {-1} Z \ cos \ omega n)] /((a ^ {-1} Z)^ 2-2(a ^ {- 1} Z \ cos \ omega n)+1)$
$ = Z(Za \ cos \ omega)/(Z ^ 2-2az \ cos \ omega + a ^ 2)$
連続的な差別化
連続微分プロパティは、時間領域で離散信号を時間に関して微分すると、Z変換が行われることを示しています。これを以下に示します。
$$ \ frac {dx(n)} {dn} =(1-Z ^ {-1})X(Z)$$Proof −
方程式のLHSを考えてみましょう- $ \ frac {dx(n)} {dn} $
$$ = \ frac {[x(n)-x(n-1)]} {[n-(n-1)]} $$$ = x(n)-X(n-1)$
$ = x(Z)-Z ^ {-1} x(Z)$
$ =(1-Z ^ {-1})x(Z)$ (したがって証明済み)
ROC:R1 <Mod(Z)<R2
例
$ x(n)= n ^ 2u(n)$で与えられる信号のZ変換を見つけましょう
プロパティによって私たちは書くことができます
$ Zz [nU(n)] = -Z \ frac {dZ [U(n)]} {dz} $
$ = -Z \ frac {d [\ frac {Z} {Z-1}]} {dZ} $
$ = Z /((Z-1)^ 2 $
$ = y(let)$
これで、プロパティを再度適用することでZ [ny]を見つけることができます。
$ Z(n、y)= -Z \ frac {dy} {dz} $
$ = -Z \ frac {d [Z /(Z-1)^ 3]} {dz} $
$ = Z(Z + 1)/(Z-1)^ 2 $
畳み込み
これは、畳み込みが離散信号形式で発生したときのシステムのZドメインの変化を示しています。これは次のように記述できます。
$ x_1(n)* x_2(n)\ longleftrightarrow X_1(Z).X_2(Z)$
Proof −
$ X(Z)= \ sum_ {n =-\ infty} ^ \ infty x(n)Z ^ {-n} $
$ = \ sum_ {n =-\ infty} ^ \ infty [\ sum_ {k =-\ infty} ^ \ infty x_1(k)x_2(nk)] Z ^ {-n} $
$ = \ sum_ {k =-\ infty} ^ \ infty x_1(k)[\ sum_n ^ \ infty x_2(nk)Z ^ {-n}] $
$ = \ sum_ {k =-\ infty} ^ \ infty x_1(k)[\ sum_ {n =-\ infty} ^ \ infty x_2(nk)Z ^ {-(nk)} Z ^ {-k}] $
nk = lとすると、上記の式は次のように記述できます。
$ X(Z)= \ sum_ {k =-\ infty} ^ \ infty x_1(k)[Z ^ {-k} \ sum_ {l =-\ infty} ^ \ infty x_2(l)Z ^ {-l }] $
$ = \ sum_ {k =-\ infty} ^ \ infty x_1(k)X_2(Z)Z ^ {-k} $
$ = X_2(Z)\ sum_ {k =-\ infty} ^ \ infty x_1(Z)Z ^ {-k} $
$ = X_1(Z).X_2(Z)$ (したがって証明済み)
ROC:$ ROC \ bigcap ROC2 $
例
2つの信号によって与えられる畳み込みを見つけましょう
$ x_1(n)= \ lbrace 3、-2,2 \ rbrace $ ...(式1)
$ x_2(n)= \ lbrace 2,0 \ leq 4 \ quadおよび\ quad 0 \ quad他の場所\ rbrace $ ...(式2)
最初の方程式のZ変換は次のように書くことができます。
$ \ sum_ {n =-\ infty} ^ \ infty x_1(n)Z ^ {-n} $
$ = 3-2Z ^ {-1} + 2Z ^ {-2} $
2番目の信号のZ変換は次のように書くことができます。
$ \ sum_ {n =-\ infty} ^ \ infty x_2(n)Z ^ {-n} $
$ = 2 + 2Z ^ {-1} + 2Z ^ {-2} + 2Z ^ {-3} + 2Z ^ {-4} $
したがって、上記の2つの信号の畳み込みは次の式で与えられます。
$ X(Z)= [x_1(Z)^ * x_2(Z)] $
$ = [3-2Z ^ {-1} + 2Z ^ {-2}] \ times [2 + 2Z ^ {-1} + 2Z ^ {-2} + 2Z ^ {-3} + 2Z ^ {-4 }] $
$ = 6 + 2Z ^ {-1} + 6Z ^ {-2} + 6Z ^ {-3} + ... \ quad ... \ quad ... $
得られた逆Z変換をとると、
$ x(n)= \ lbrace 6,2,6,6,6,0,4 \ rbrace $
初期値の定理
x(n)が因果シーケンスであり、そのZ変換がX(z)である場合、初期値の定理は次のように記述できます。
$ X(n)(at \ quad n = 0)= \ lim_ {z \ to \ infty} X(z)$
Proof −私たちはそれを知っています、
$ X(Z)= \ sum_ {n = 0} ^ \ infty x(n)Z ^ {-n} $
上記のシリーズを拡張すると、次のようになります。
$ = X(0)Z ^ 0 + X(1)Z ^ {-1} + X(2)Z ^ {-2} + ... \ quad ... $
$ = X(0)\ times 1 + X(1)Z ^ {-1} + X(2)Z ^ {-2} + ... \ quad ... $
上記の場合、Z→∞の場合、$ Z ^ {-n} \ rightarrow 0 $(n> 0であるため)
したがって、私たちは言うことができます。
$ \ lim_ {z \ to \ infty} X(z)= X(0)$ (したがって証明済み)
最終値の定理
最終値定理は、信号のZ変換がX(Z)として表され、極がすべて円の内側にある場合、その最終値はx(n)またはX(∞)として表され、次のように記述できると述べています。 −
$ X(\ infty)= \ lim_ {n \ to \ infty} X(n)= \ lim_ {z \ to 1} [X(Z)(1-Z ^ {-1})] $
Conditions −
- 因果システムにのみ適用されます。
- $ X(Z)(1-Z ^ {-1})$は、Z平面の単位円の内側に極を持っている必要があります。
Proof −私たちはそれを知っています
$ Z ^ + [x(n + 1)-x(n)] = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {-n} [x(n + 1)-x (n)] $
$ \ Rightarrow Z ^ + [x(n + 1)]-Z ^ + [x(n)] = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {-n} [x (n + 1)-x(n)] $
$ \ Rightarrow Z [X(Z)^ + -x(0)]-X(Z)^ + = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {-n} [x (n + 1)-x(n)] $
ここでは、片側Z変換の高度なプロパティを適用できます。したがって、上記の式は次のように書き直すことができます。
$ Z ^ + [x(n + 1)] = Z [X(2)^ + -x(0)Z ^ 0] = Z [X(Z)^ + -x(0)] $
上記の式にz = 1を入れると、上記の式を展開できます。
$ \ lim_ {k \ to \ infty} {[x(1)-x(0)+ x(6)-x(1)+ x(3)-x(2)+ ... \ quad .. .. \ quad ... + x(x + 1)-x(k)]} $
これは次のように定式化できます。
$ X(\ infty)= \ lim_ {n \ to \ infty} X(n)= \ lim_ {z \ to 1} [X(Z)(1-Z ^ {-1})] $ (したがって証明済み)
例
信号が次の式で与えられるx(n)の初期値と最終値を見つけましょう。
$ X(Z)= 2 + 3Z ^ {-1} + 4Z ^ {-2} $
Solution −まず、定理を適用して信号の初期値を求めます。
$ x(0)= \ lim_ {z \ to \ infty} X(Z)$
$ = \ lim_ {z \ to \ infty} [2 + 3Z ^ {-1} + 4Z ^ {-2}] $
$ = 2 +(\ frac {3} {\ infty})+(\ frac {4} {\ infty})= 2 $
ここで、定理を適用した信号の最終値を見つけましょう。
$ x(\ infty)= \ lim_ {z \ to \ infty} [(1-Z ^ {-1})X(Z)] $
$ = \ lim_ {z \ to \ infty} [(1-Z ^ {-1})(2 + 3Z ^ {-1} + 4Z ^ {-2})] $
$ = \ lim_ {z \ to \ infty} [2 + Z ^ {-1} + Z ^ {-2} -4Z ^ {-3}] $
$ = 2 + 1 + 1-4 = 0 $
Some other properties of Z-transform are listed below −
頻度の差別化
離散信号が時間に関して微分されると、信号のZドメインに変化が生じます。
$ nx(n)\ longleftrightarrow -Z \ frac {dX(z)} {dz} $
そのROCは次のように書くことができます。
$ r_2 <Mod(Z)<r_1 $
例
Zドメインの離散信号が$ x(n)\ longleftrightarrow X(Z)= log(1 + aZ ^ {-1})$で与えられる、周波数の微分によってx(n)の値を見つけましょう。
プロパティによって、私たちはそれを書くことができます
$ nx(n)\ longleftrightarrow -Z \ frac {dx(Z)} {dz} $
$ = -Z [\ frac {-aZ ^ {-2}} {1 + aZ ^ {-1}}] $
$ =(aZ ^ {-1})/(1 + aZ ^ {-1})$
$ = 1-1 /(1 + aZ ^ {-1})$
$ nx(n)= \ delta(n)-(-a)^ nu(n)$
$ \ Rightarrow x(n)= 1 / n [\ delta(n)-(-a)^ nu(n)] $
時間の掛け算
離散信号レベルで乗算が行われると、信号のZドメインが変化します。
$ x_1(n).x_2(n)\ longleftrightarrow(\ frac {1} {2 \ Pi j})[X1(Z)* X2(Z)] $
時間内の接合
これは、Zドメインでの共役離散信号の表現を示しています。
$ X ^ *(n)\ longleftrightarrow X ^ *(Z ^ *)$