DSP-信号微分の操作
信号に対して実行される2つの非常に重要な操作は、微分と積分です。
差別化
任意の信号x(t)の微分は、時間に対するその信号の勾配表現を意味します。数学的には、次のように表されます。
$$ x(t)\ rightarrow \ frac {dx(t)} {dt} $$OPAMPの差別化の場合、この方法論は非常に役立ちます。式を使用するのではなく、信号をグラフィカルに簡単に区別できます。ただし、条件は、信号が長方形または三角形のタイプである必要があることです。これはほとんどの場合に発生します。
| 元の信号 | 分化した信号 |
|---|---|
| ランプ | ステップ |
| ステップ | インパルス |
| インパルス | 1 |
上記の表は、微分後の信号の状態を示しています。たとえば、ランプ信号は微分後にステップ信号に変換されます。同様に、単位ステップ信号はインパルス信号になります。
例
与えられた信号を$ x(t)= 4 [r(t)-r(t-2)] $とします。この信号をプロットすると、下図の左側のようになります。今、私たちの目的は、与えられた信号を区別することです。
まず、与えられた方程式の微分を開始します。微分後のランプ信号が単位ステップ信号を与えることがわかっています。
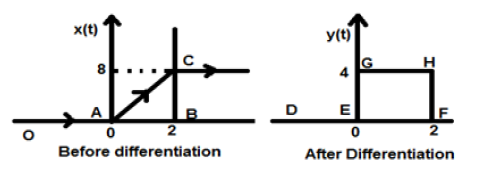
したがって、結果の信号y(t)は次のように書くことができます。
$ y(t)= \ frac {dx(t)} {dt} $
$ = \ frac {d4 [r(t)-r(t-2)]} {dt} $
$ = 4 [u(t)-u(t-2)] $
これで、この信号が最終的にプロットされます。これは、上の図の右側に示されています。