DSP-シグナルスケーリングの操作

信号のスケーリングとは、定数に信号の時間または振幅を掛けることを意味します。

タイムスケーリング

定数が時間軸に乗算される場合、それは時間スケーリングとして知られています。これは数学的に次のように表すことができます。

$ x（t）\ rightarrow y（t）= x（\ alpha t）$または$ x（\ frac {t} {\ alpha}）$; ここで、α≠0

したがって、y軸が同じである場合、x軸の大きさは、定数の符号（正または負）に応じて増減します。したがって、スケーリングは、以下で説明するように2つのカテゴリに分類することもできます。

アルファがゼロより大きい場合は常に、信号の振幅がアルファで除算されますが、Y軸の値は同じままです。これは時間圧縮として知られています。

Example

次の図のように示されている信号x（t）を考えてみましょう。alphaの値を2とすると、y（t）はx（2t）になります。これは、次の図に示されています。

明らかに、上記の図から、y軸の時間の大きさは同じままですが、x軸の振幅が4から2に減少していることがわかります。したがって、これは時間圧縮の場合です。

時間を一定のアルファで割ると、信号のY軸の大きさがアルファ倍になり、X軸の大きさはそのままになります。したがって、これを時間拡張型信号と呼びます。

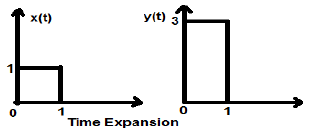
Example

振幅1の方形信号x（t）を考えてみましょう。定数3で時間スケーリングすると、$ x（t）\ rightarrow y（t）\ rightarrow x（\ frac {t} {3} ）$の場合、信号の振幅は次の図に示すように3倍に変更されます。

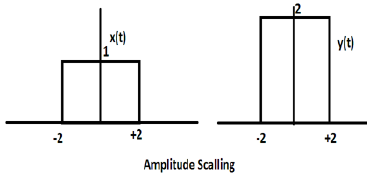
定数と信号の振幅を乗算すると、振幅スケーリングが発生します。定数の符号に応じて、振幅スケーリングまたは減衰のいずれかになります。方形波信号x（t）=Π（t / 4）を考えてみましょう。

別の関数y（t）=2Π（t / 4）を定義するとします。この場合、y軸の値は2倍になり、時間軸の値はそのままになります。以下の図に、を示します。

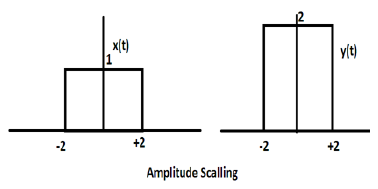
z（t）=0.5Π（t / 4）であるz（t）として定義される別の方形波関数について考えてみます。ここで、関数z（t）の振幅はx（t）の振幅の半分になります。つまり、時間軸は同じままで、振幅軸は半分になります。これは、次の図に示されています。