デジタル信号処理-信号-定義

定義

情報を運ぶものはすべて信号と呼ぶことができます。また、時間、温度、圧力、または音声信号やビデオ信号などの独立変数によって変化する物理量として定義することもできます。

信号の特性（振幅、形状、位相、周波数など）が変化する動作プロセスは、信号処理と呼ばれます。

Note−メイン信号に干渉する不要な信号は、ノイズと呼ばれます。したがって、ノイズも信号ですが、望ましくありません。

それらの表現と処理に従って、信号はさまざまなカテゴリに分類できます。詳細については、以下で説明します。

連続時間信号は、時間の連続に沿って定義されるため、連続独立変数で表されます。連続時間信号は、しばしばアナログ信号と呼ばれます。

このタイプの信号は、振幅と時間の両方で連続性を示します。これらは、各時点で値を持ちます。正弦関数と余弦関数は、連続時間信号の最良の例です。

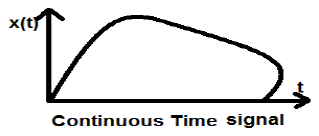
上記の信号は、各瞬間の信号の値を取得できるため、連続時間信号の例です。

離散時間で定義される信号は、離散信号と呼ばれます。したがって、すべての独立変数には異なる値があります。したがって、それらは一連の数字として表されます。

音声信号とビデオ信号には、連続時間形式と離散時間形式の両方で表現できる特権があります。特定の状況下では、それらは同一です。振幅も離散的な特性を示します。この完璧な例はデジタル信号です。その振幅と時間は両方とも離散的です。

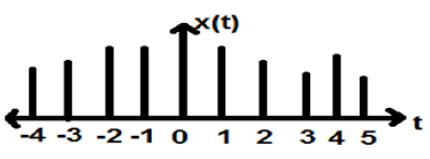
上の図は、ある期間にわたる離散信号の離散振幅特性を示しています。数学的には、これらのタイプの信号は次のように定式化できます。

$$ x = \ left \ {x \ left [n \ right] \ right \}、\ quad- \ infty <n <\ infty $$

ここで、nは整数です。

これは数xのシーケンスであり、シーケンスのn^番目の数はx [n]として表されます。