制御システム-ブロック図代数
ブロック図代数は、ブロック図の基本要素に関係する代数に他なりません。この代数は、代数方程式の絵画的表現を扱います。
ブロックの基本的な接続
2つのブロック間の接続には3つの基本的なタイプがあります。
直列接続
直列接続は、 cascade connection。次の図では、伝達関数$ G_1(s)$と$ G_2(s)$を持つ2つのブロックが直列に接続されています。

この組み合わせの場合、出力$ Y(s)$は次のようになります。
$$ Y(s)= G_2(s)Z(s)$$
ここで、$ Z(s)= G_1(s)X(s)$
$$ \ Rightarrow Y(s)= G_2(s)[G_1(s)X(s)] = G_1(s)G_2(s)X(s)$$
$$ \ Rightarrow Y(s)= \ lbrace G_1(s)G_2(s)\ rbrace X(s)$$
この方程式を、出力方程式の標準形式$ Y(s)= G(s)X(s)$と比較します。ここで、$ G(s)= G_1(s)G_2(s)$。
つまり、 series connection1つのブロックで2つのブロックの。この単一ブロックの伝達関数はproduct of the transfer functionsそれらの2つのブロックの。同等のブロック図を以下に示します。
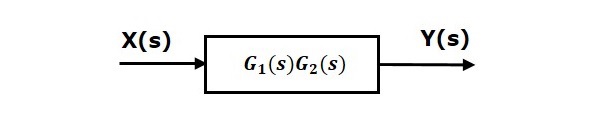
同様に、「n」ブロックの直列接続を単一のブロックで表すことができます。この単一ブロックの伝達関数は、これらすべての「n」ブロックの伝達関数の積です。
並列接続
で接続されているブロック parallel があります same input。次の図では、伝達関数$ G_1(s)$と$ G_2(s)$を持つ2つのブロックが並列に接続されています。これら2つのブロックの出力は、加算点に接続されます。

この組み合わせの場合、出力$ Y(s)$は次のようになります。
$$ Y(s)= Y_1(s)+ Y_2(s)$$
ここで、$ Y_1(s)= G_1(s)X(s)$および$ Y_2(s)= G_2(s)X(s)$
$$ \ Rightarrow Y(s)= G_1(s)X(s)+ G_2(s)X(s)= \ lbrace G_1(s)+ G_2(s)\ rbrace X(s)$$
この方程式を、出力方程式の標準形式$ Y(s)= G(s)X(s)$と比較します。
ここで、$ G(s)= G_1(s)+ G_2(s)$です。
つまり、 parallel connection1つのブロックで2つのブロックの。この単一ブロックの伝達関数はsum of the transfer functionsそれらの2つのブロックの。同等のブロック図を以下に示します。

同様に、「n」ブロックの並列接続を単一のブロックで表すことができます。この単一ブロックの伝達関数は、これらすべての「n」ブロックの伝達関数の代数和です。
フィードバック接続
前の章で説明したように、2つのタイプがあります feedback—正のフィードバックと負のフィードバック。次の図は、負帰還制御システムを示しています。ここでは、伝達関数$ G(s)$と$ H(s)$を持つ2つのブロックが閉ループを形成しています。

加算点の出力は-
$$ E(s)= X(s)-H(s)Y(s)$$
出力$ Y(s)$は-
$$ Y(s)= E(s)G(s)$$
上記の式に$ E(s)$の値を代入します。
$$ Y(s)= \ left \ {X(s)-H(s)Y(s)\ rbrace G(s)\ right \} $$
$$ Y(s)\ left \ {1 + G(s)H(s)\ rbrace = X(s)G(s)\ right \} $$
$$ \ Rightarrow \ frac {Y(s)} {X(s)} = \ frac {G(s)} {1 + G(s)H(s)} $$
したがって、負帰還閉ループ伝達関数は$ \ frac {G(s)} {1 + G(s)H(s)} $です。
これは、2つのブロックの負のフィードバック接続を1つのブロックで表すことができることを意味します。この単一ブロックの伝達関数は、負帰還の閉ループ伝達関数です。同等のブロック図を以下に示します。

同様に、1つのブロックで2つのブロックの正のフィードバック接続を表すことができます。この単一ブロックの伝達関数は、正のフィードバックの閉ループ伝達関数です。つまり、$ \ frac {G(s)} {1-G(s)H(s)} $
ポイントを合計するためのブロック図代数
ブロックに関して加算点をシフトする可能性は2つあります-
- ブロック後の合計ポイントのシフト
- ブロックの前の合計ポイントのシフト
ここで、上記の2つのケースでどのような調整を行う必要があるかを1つずつ見ていきましょう。
ブロック後の合計ポイントのシフト
次の図に示すブロック図について考えてみます。ここでは、加算点はブロックの前にあります。

加算点には、2つの入力$ R(s)$と$ X(s)$があります。その出力は$ \ left \ {R(s)+ X(s)\ right \} $です。
したがって、ブロック$ G(s)$への入力は$ \ left \ {R(s)+ X(s)\ right \} $であり、その出力は–です。
$$ Y(s)= G(s)\ left \ {R(s)+ X(s)\ right \} $$
$ \ Rightarrow Y(s)= G(s)R(s)+ G(s)X(s)$ (Equation 1)
ここで、合計ポイントをブロックの後にシフトします。このブロック図を次の図に示します。

ブロック$ G(s)$の出力は$ G(s)R(s)$です。
加算点の出力は次のとおりです。
$ Y(s)= G(s)R(s)+ X(s)$ (Equation 2)
式1と式2を比較してください。
最初の項$ 'G(s)R(s)' $は、両方の方程式で同じです。ただし、第2期には違いがあります。2番目の項も同じにするために、もう1つのブロック$ G(s)$が必要です。入力$ X(s)$があり、このブロックの出力は$ X(s)$ではなく加算点への入力として与えられます。このブロック図を次の図に示します。
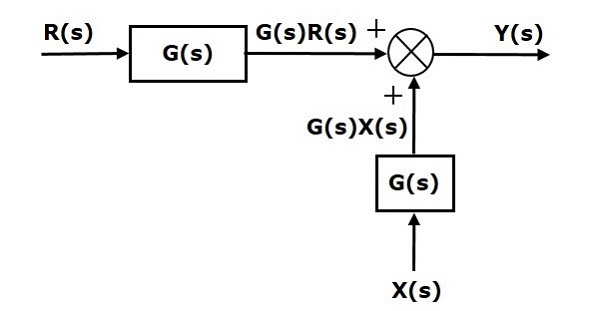
ブロック前の加算点のシフト
次の図に示すブロック図について考えてみます。ここでは、加算点はブロックの後にあります。

このブロック図の出力は-
$ Y(s)= G(s)R(s)+ X(s)$ (Equation 3)
ここで、合計ポイントをブロックの前にシフトします。このブロック図を次の図に示します。

このブロック図の出力は-
$ Y(S)= G(s)R(s)+ G(s)X(s)$ (Equation 4)
式3と式4を比較してください。
最初の項$ 'G(s)R(s)' $は両方の方程式で同じです。ただし、第2期には違いがあります。2番目の項も同じにするために、もう1つのブロック$ \ frac {1} {G(s)} $が必要です。入力$ X(s)$があり、このブロックの出力は$ X(s)$ではなく加算点への入力として与えられます。このブロック図を次の図に示します。

離陸地点のブロック図代数
ブロックに関してテイクオフポイントをシフトする可能性は2つあります-
- ブロック後の離陸地点のシフト
- ブロック前の離陸地点の移動
ここで、上記の2つのケースでどのような取り決めが行われるのかを1つずつ見ていきましょう。
ブロック後の離陸地点のシフト
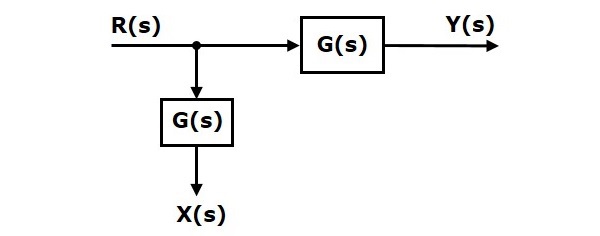
次の図に示すブロック図について考えてみます。この場合、離陸地点はブロックの前にあります。

ここで、$ X(s)= R(s)$および$ Y(s)= G(s)R(s)$
ブロックの後にテイクオフポイントをシフトすると、出力$ Y(s)$は同じになります。ただし、$ X(s)$の値には違いがあります。したがって、同じ$ X(s)$値を取得するには、もう1つのブロック$ \ frac {1} {G(s)} $が必要です。入力は$ Y(s)$で、出力は$ X(s)$です。このブロック図を次の図に示します。

ブロック前の離陸地点の移動
次の図に示すブロック図について考えてみます。ここでは、離陸地点はブロックの後にあります。

ここで、$ X(s)= Y(s)= G(s)R(s)$
ブロックの前でテイクオフポイントをシフトすると、出力$ Y(s)$は同じになります。ただし、$ X(s)$の値には違いがあります。したがって、同じ$ X(s)$値を取得するには、もう1つのブロック$ G(s)$が必要です。入力は$ R(s)$で、出力は$ X(s)$です。このブロック図を次の図に示します。