機械システムの電気的アナロジー

2つのシステムは analogous 次の2つの条件が満たされている場合。

• 2つのシステムは物理的に異なります
• これら2つのシステムの微分方程式モデリングは同じです

電気システムと機械システムは、物理的に異なる2つのシステムです。並進機械システムの電気的アナロジーには2つのタイプがあります。それらは力電圧のアナロジーと力電流のアナロジーです。

力の電圧のアナロジー

力の電圧のアナロジーでは、の数式 translational mechanical system 電気システムのメッシュ方程式と比較されます。

次の図に示すように、次の並進機械システムについて考えてみます。

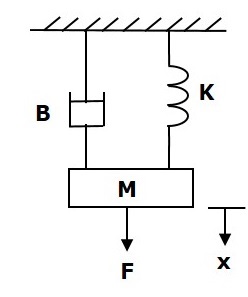
ザ・ force balanced equation このシステムの

$$ F = F_m + F_b + F_k $$

$ \ Rightarrow F = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} + B \ frac {\ text {d} x} {\ text {d} t} + Kx $ (Equation 1)

次の図に示すように、次の電気システムについて考えてみます。この回路は、抵抗、インダクタ、コンデンサで構成されています。これらの電気素子はすべて直列に接続されています。この回路に印加される入力電圧は$ V $ボルトで、回路を流れる電流は$ i $アンペアです。

この回路のメッシュ方程式は次のとおりです。

$ V = Ri + L \ frac {\ text {d} i} {\ text {d} t} + \ frac {1} {c} \ int idt $ (Equation 2)

式2の$ i = \ frac {\ text {d} q} {\ text {d} t} $を代入します。

$$ V = R \ frac {\ text {d} q} {\ text {d} t} + L \ frac {\ text {d} ^ 2q} {\ text {d} t ^ 2} + \ frac { q} {C} $$

$ \ Rightarrow V = L \ frac {\ text {d} ^ 2q} {\ text {d} t ^ 2} + R \ frac {\ text {d} q} {\ text {d} t} + \ left （\ frac {1} {c} \ right）q $ (Equation 3)

式1と式3を比較することにより、並進機械システムと電気システムの類似した量が得られます。次の表は、これらの類似した数量を示しています。

並進機械システム	電気システム
Force（F）	電圧（V）
質量（M）	インダクタンス（L）
摩擦係数（B）	抵抗（R）
ばね定数（K）	静電容量の逆数$（\ frac {1} {c}）$
変位（x）	Charge（q）
速度（v）	Current（i）

同様に、回転機械システムにはトルク電圧のアナロジーがあります。ここで、このアナロジーについて説明しましょう。

トルク電圧のアナロジー

この例えでは、の数式は rotational mechanical system 電気システムのメッシュ方程式と比較されます。

回転機械システムを次の図に示します。

トルクバランス方程式は

$$ T = T_j + T_b + T_k $$

$ \ Rightarrow T = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} + B \ frac {\ text {d} \ theta} {\ text {d} t} + k \ theta $ (Equation 4)

式4と式3を比較することにより、回転機械システムと電気システムの類似した量が得られます。次の表は、これらの類似した数量を示しています。

回転機械システム	電気システム
トルク（T）	電圧（V）
慣性モーメント（J）	インダクタンス（L）
回転摩擦係数（B）	抵抗（R）
ねじりばね定数（K）	静電容量の逆数$（\ frac {1} {c}）$
角変位（θ）	Charge（q）
角速度（ω）	Current（i）

力の現在のアナロジー

力の電流のアナロジーでは、の数式 translational mechanical system 電気系統の節点方程式と比較されます。

次の図に示すように、次の電気システムについて考えてみます。この回路は、電流源、抵抗、インダクタ、コンデンサで構成されています。これらの電気素子はすべて並列に接続されています。

節点方程式は

$ i = \ frac {V} {R} + \ frac {1} {L} \ int Vdt + C \ frac {\ text {d} V} {\ text {d} t} $ (Equation 5)

式5の$ V = \ frac {\ text {d} \ Psi} {\ text {d} t} $を代入します。

$$ i = \ frac {1} {R} \ frac {\ text {d} \ Psi} {\ text {d} t} + \ left（\ frac {1} {L} \ right）\ Psi + C \ frac {\ text {d} ^ 2 \ Psi} {\ text {d} t ^ 2} $$

$ \ Rightarrow i = C \ frac {\ text {d} ^ 2 \ Psi} {\ text {d} t ^ 2} + \ left（\ frac {1} {R} \ right）\ frac {\ text { d} \ Psi} {\ text {d} t} + \ left（\ frac {1} {L} \ right）\ Psi $ (Equation 6)

式1と式6を比較することにより、並進機械システムと電気システムの類似した量が得られます。次の表は、これらの類似した数量を示しています。

並進機械システム	電気システム
Force（F）	Current（i）
質量（M）	静電容量（C）
摩擦係数（B）	抵抗の逆数$（\ frac {1} {R}）$
ばね定数（K）	インダクタンスの逆数$（\ frac {1} {L}）$
変位（x）	磁束（ψ）
速度（v）	電圧（V）

同様に、回転機械システムにはトルク電流のアナロジーがあります。ここで、このアナロジーについて説明しましょう。

トルク電流のアナロジー

このアナロジーでは、の数式 rotational mechanical system 電気システムの節点メッシュ方程式と比較されます。

式4と式6を比較することにより、回転機械システムと電気システムの類似した量が得られます。次の表は、これらの類似した数量を示しています。

回転機械システム	電気システム
トルク（T）	Current（i）
慣性モーメント（J）	静電容量（C）
回転摩擦係数（B）	抵抗の逆数$（\ frac {1} {R}）$
ねじりばね定数（K）	インダクタンスの逆数$（\ frac {1} {L}）$
角変位（θ）	磁束（ψ）
角速度（ω）	電圧（V）

この章では、機械システムの電気的アナロジーについて説明しました。これらのアナロジーは、類似の電気システムから機械システムのような非電気システムを研究および分析するのに役立ちます。