制御システム-ブロック図

ブロックダイアグラムは、単一のブロックまたはブロックの組み合わせで構成されます。これらは、制御システムを図で表すために使用されます。

ブロック図の基本要素

ブロックダイアグラムの基本要素は、ブロック、加算ポイント、およびテイクオフポイントです。これらの要素を特定するために、次の図に示すような閉ループ制御システムのブロック図を考えてみましょう。

上記のブロック図は、伝達関数G（s）とH（s）を持つ2つのブロックで構成されています。また、1つの加算ポイントと1つの離陸ポイントがあります。矢印は信号の流れの方向を示しています。これらの要素を1つずつ説明していきましょう。

ブロック

コンポーネントの伝達関数はブロックで表されます。ブロックには単一の入力と単一の出力があります。

次の図は、入力X（s）、出力Y（s）、および伝達関数G（s）を持つブロックを示しています。

伝達関数、$ G（s）= \ frac {Y（s）} {X（s）} $

$$ \ Rightarrow Y（s）= G（s）X（s）$$

ブロックの出力は、ブロックの伝達関数に入力を掛けることによって得られます。

加算点

加算点は、内部に十字（X）が付いた円で表されます。2つ以上の入力と1つの出力があります。入力の代数和を生成します。また、入力の極性に基づいて、入力の合計または減算、あるいは合計と減算の組み合わせを実行します。これらの3つの操作を1つずつ見ていきましょう。

次の図は、2つの入力（A、B）と1つの出力（Y）の合計点を示しています。ここで、入力AとBは正の符号を持っています。したがって、加算点は出力Yを生成します。sum of A and B.

つまり、Y = A + Bです。

次の図は、2つの入力（A、B）と1つの出力（Y）の合計点を示しています。ここで、入力AとBは反対の符号を持っています。つまり、Aは正の符号を持ち、Bは負の符号を持っています。したがって、加算点は出力を生成しますY として difference of A and B。

Y = A +（-B）= A--B。

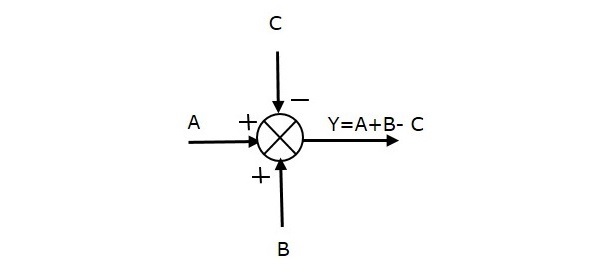
次の図は、3つの入力（A、B、C）と1つの出力（Y）の合計点を示しています。ここで、入力AとBは正の符号を持ち、Cは負の符号を持っています。したがって、加算点は出力を生成しますY なので

Y = A + B +（− C）= A + B −C。

離陸地点

テイクオフポイントは、同じ入力信号が複数のブランチを通過できるポイントです。つまり、テイクオフポイントを使用して、同じ入力を1つ以上のブロックに適用し、ポイントを合計することができます。

次の図では、テイクオフポイントを使用して、同じ入力R（s）をさらに2つのブロックに接続しています。

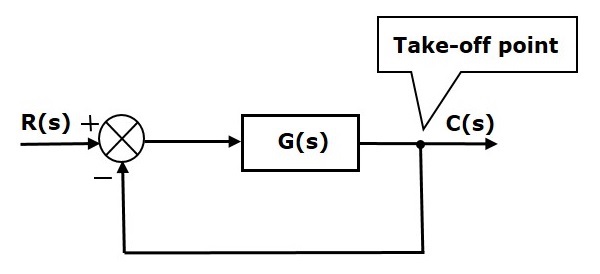
次の図では、テイクオフポイントを使用して、入力の1つとして出力C（s）を加算ポイントに接続しています。

電気システムのブロック図表現

このセクションでは、電気システムをブロック図で表現しましょう。電気システムには、主に3つの基本要素が含まれています—resistor, inductor and capacitor。

次の図に示すような一連のRLC回路について考えてみます。ここで、V _i（t）とV _o（t）は入力電圧と出力電圧です。i（t）を回路を流れる電流とします。この回路は時間領域にあります。

この回路にラプラス変換を適用することにより、回路はsドメインになります。回路は次の図のようになります。

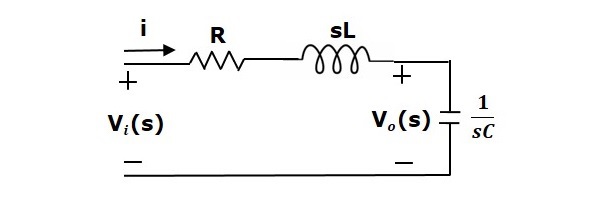
上記の回路から、次のように書くことができます。

$$ I（s）= \ frac {V_i（s）-V_o（s）} {R + sL} $$

$ \ Rightarrow I（s）= \ left \ {\ frac {1} {R + sL} \ right \} \ left \ {V_i（s）-V_o（s）\ right \} $ (Equation 1)

$ V_o（s）= \ left（\ frac {1} {sC} \ right）I（s）$ (Equation 2)

ここで、これら2つの方程式のブロック図を個別に描画してみましょう。次に、これらのブロック図を適切に組み合わせて、一連のRLC回路（sドメイン）の全体的なブロック図を取得します。

式1は、伝達関数$ \ frac {1} {R + sL} $を持つブロックを使用して実装できます。このブロックの入力と出力は$ \ left \ {V_i（s）-V_o（s）\ right \} $と$ I（s）$です。$ \ left \ {V_i（s）-V_o（s）\ right \} $を取得するには、加算点が必要です。式1のブロック図を次の図に示します。