機械システムのモデリング
この章では、 differential equation modeling機械システムの。モーションのタイプに基づいて、2つのタイプの機械システムがあります。
- 並進機械システム
- 回転機械システム
並進機械システムのモデリング
並進機械システムは、 straight line。これらのシステムは、主に3つの基本要素で構成されています。それらは、マス、スプリング、ダッシュポットまたはダンパーです。
並進機械システムに力が加えられると、システムの質量、弾性、摩擦による反対の力に対抗します。加えられた力と反対の力は反対方向にあるため、システムに作用する力の代数和はゼロです。ここで、これら3つの要素が個別に対抗する力を見てみましょう。
質量
質量は体の特性であり、 kinetic energy。質量のある物体に力が加わった場合M、それからそれは質量による反対の力によって反対されます。この反対の力は、体の加速度に比例します。弾性と摩擦は無視できると仮定します。

$$ F_m \ propto \:a $$
$$ \ Rightarrow F_m = Ma = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} $$
$$ F = F_m = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} $$
どこ、
F 加えられる力です
Fm 質量による反対の力です
M 質量です
a 加速です
x 変位です
春
春は要素であり、 potential energy。ばねに力が加わった場合K、それからそれはばねの弾性による反対の力によって反対されます。この反対の力は、ばねの変位に比例します。質量と摩擦はごくわずかであると仮定します。

$$ F \ propto \:x $$
$$ \ Rightarrow F_k = Kx $$
$$ F = F_k = Kx $$
どこ、
F 加えられる力です
Fk ばねの弾性による反対の力です
K ばね定数です
x 変位です
ダッシュポット
ダッシュポットに力が加えられた場合 B、それからそれはのために反対の力によって反対されます frictionダッシュポットの。この反対の力は、体の速度に比例します。質量と弾性は無視できると仮定します。

$$ F_b \ propto \:\ nu $$
$$ \ Rightarrow F_b = B \ nu = B \ frac {\ text {d} x} {\ text {d} t} $$
$$ F = F_b = B \ frac {\ text {d} x} {\ text {d} t} $$
どこ、
Fb ダッシュポットの摩擦による反対の力です
B は摩擦係数です
v 速度です
x 変位です
回転機械システムのモデリング
回転機械システムは、固定軸を中心に移動します。これらのシステムは、主に3つの基本要素で構成されています。それらはmoment of inertia, torsional spring そして dashpot。
回転機械システムにトルクが加えられると、システムの慣性モーメント、弾性、摩擦により、反対のトルクが発生します。加えられたトルクと反対のトルクは反対方向であるため、システムに作用するトルクの代数和はゼロです。ここで、これら3つの要素が個別に対抗するトルクを見てみましょう。
慣性モーメント
並進機械システムでは、質量は運動エネルギーを蓄えます。同様に、回転機械システムでは、慣性モーメントが保存されますkinetic energy。
慣性モーメントのある物体にトルクを加えた場合 J、次に、慣性モーメントによる反対のトルクが反対になります。この反対のトルクは、物体の角加速度に比例します。弾性と摩擦は無視できると仮定します。

$$ T_j \ propto \:\ alpha $$
$$ \ Rightarrow T_j = J \ alpha = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} $$
$$ T = T_j = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} $$
どこ、
T 加えられるトルクです
Tj は慣性モーメントによる逆トルクです
J 慣性モーメントです
α 角加速度です
θ 角変位です
ねじりばね
並進機械システムでは、ばねは位置エネルギーを蓄えます。同様に、回転機械システムでは、ねじりばねはpotential energy。
ねじりばねにトルクがかかる場合 K、次に、ねじりばねの弾性による反対のトルクによって反対されます。この反対のトルクは、ねじりばねの角変位に比例します。慣性モーメントと摩擦は無視できると仮定します。
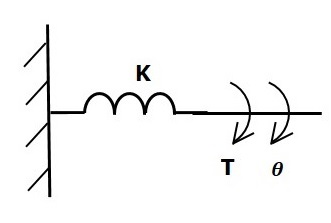
$$ T_k \ propto \:\ theta $$
$$ \ Rightarrow T_k = K \ theta $$
$$ T = T_k = K \ theta $$
どこ、
T 加えられるトルクです
Tk ねじりばねの弾性による逆トルクです
K ねじりばね定数です
θ 角変位です
ダッシュポット
ダッシュポットにトルクがかかっている場合 B、それからそれは反対のトルクによって反対されます rotational frictionダッシュポットの。この反対のトルクは、物体の角速度に比例します。慣性モーメントと弾性は無視できると仮定します。
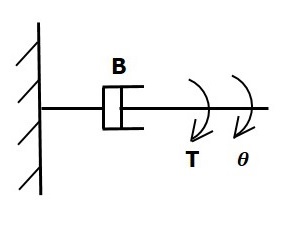
$$ T_b \ propto \:\ omega $$
$$ \ Rightarrow T_b = B \ omega = B \ frac {\ text {d} \ theta} {\ text {d} t} $$
$$ T = T_b = B \ frac {\ text {d} \ theta} {\ text {d} t} $$
どこ、
Tb ダッシュポットの回転摩擦による反対のトルクです
B は回転摩擦係数です
ω 角速度です
θ 角変位です