制御システム-クイックガイド

制御システムは、出力を制御することによって目的の応答を提供するシステムです。次の図は、制御システムの簡単なブロック図を示しています。

ここでは、制御システムは単一のブロックで表されます。出力はさまざまな入力によって制御されるため、制御システムはこの名前になりました。この入力を何らかのメカニズムで変化させます。開ループおよび閉ループ制御システムに関する次のセクションでは、制御システム内のブロックと、目的の応答を得るためにこの入力を変更する方法について詳しく説明します。

Examples −信号制御システム、洗濯機

Traffic lights control system制御システムの例です。ここでは、一連の入力信号がこの制御システムに適用され、出力は一定期間点灯する3つのライトの1つです。この間、他の2つのライトは消灯します。特定のジャンクションでの交通調査に基づいて、ライトのオンとオフの時間を決定できます。したがって、入力信号が出力を制御します。したがって、信号制御システムは時間ベースで動作します。

制御システムの分類

いくつかのパラメータに基づいて、制御システムを次の方法に分類できます。

連続時間および離散時間制御システム

• 制御システムは、に基づいて連続時間制御システムと離散時間制御システムに分類できます。 type of the signal 中古。

• に continuous time制御システムでは、すべての信号が時間的に連続しています。しかし、discrete time 制御システムには、1つ以上の離散時間信号が存在します。

SISOおよびMIMO制御システム

• 制御システムは、SISO制御システムとMIMO制御システムに基づいて分類できます。 number of inputs and outputs 現在。

• SISO（単一入力および単一出力）制御システムには、1つの入力と1つの出力があります。一方、MIMO （複数の入力と複数の出力）制御システムには、複数の入力と複数の出力があります。

開ループおよび閉ループ制御システム

制御システムは、に基づいて開ループ制御システムと閉ループ制御システムに分類できます。 feedback path。

に open loop control systems、出力は入力にフィードバックされません。したがって、制御アクションは目的の出力とは無関係です。

次の図は、開ループ制御システムのブロック図を示しています。

ここでは、入力がコントローラに適用され、それが作動信号または制御信号を生成します。この信号は、制御対象のプラントまたはプロセスへの入力として提供されます。したがって、プラントは制御された出力を生成します。先に説明した信号制御システムは、開ループ制御システムの一例です。

に closed loop control systems、出力は入力にフィードバックされます。したがって、制御アクションは目的の出力に依存します。

次の図は、負帰還閉ループ制御システムのブロック図を示しています。

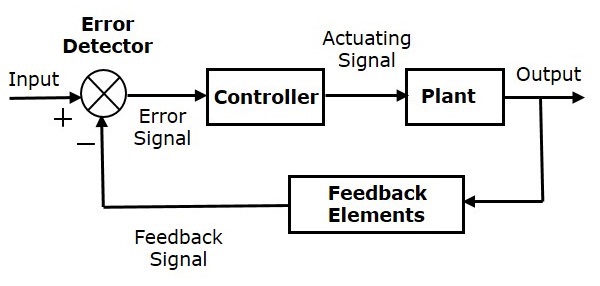
エラー検出器は、入力信号とフィードバック信号の差であるエラー信号を生成します。このフィードバック信号は、システム全体の出力をこのブロックへの入力と見なすことにより、ブロック（フィードバック要素）から取得されます。直接入力の代わりに、エラー信号がコントローラーへの入力として適用されます。

したがって、コントローラーはプラントを制御する作動信号を生成します。この組み合わせでは、制御システムの出力は、目的の応答が得られるまで自動的に調整されます。したがって、閉ループ制御システムは自動制御システムとも呼ばれます。入力にセンサーを備えた信号機制御システムは、閉ループ制御システムの一例です。

開ループ制御システムと閉ループ制御システムの違いを次の表に示します。

開ループ制御システム	閉ループ制御システム
制御アクションは、目的の出力とは無関係です。	制御アクションは、目的の出力に依存します。
フィードバックパスが存在しません。	フィードバックパスが存在します。
これらは、 non-feedback control systems。	これらは、 feedback control systems。
設計が簡単。	設計が難しい。
これらは経済的です。	これらはコストがかかります。
不正確。	正確。

出力または出力の一部が入力側に返され、システム入力の一部として利用される場合、それは次のように知られています。 feedback。フィードバックは、制御システムのパフォーマンスを向上させるために重要な役割を果たします。この章では、フィードバックの種類とフィードバックの効果について説明します。

フィードバックの種類

フィードバックには2つのタイプがあります-

• 正のフィードバック
• 負帰還

正のフィードバック

正のフィードバックは、参照入力を追加します。 $R(s)$およびフィードバック出力。次の図は、のブロック図を示しています。positive feedback control system。

伝達関数の概念については、後の章で説明します。とりあえず、正帰還制御システムの伝達関数は、

$T=\frac{G}{1-GH}$ （式1）

どこ、

• T は、正のフィードバック制御システムの伝達関数または全体的なゲインです。

• G は、周波数の関数である開ループゲインです。

• H はフィードバックパスのゲインであり、周波数の関数です。

負帰還

負帰還は、基準入力間の誤差を減らします。 $R(s)$およびシステム出力。次の図は、のブロック図を示しています。negative feedback control system。

負帰還制御システムの伝達関数は、

$T=\frac{G}{1+GH}$ （式2）

どこ、

• T は、負帰還制御システムの伝達関数または全体的なゲインです。

• G は、周波数の関数である開ループゲインです。

• H はフィードバックパスのゲインであり、周波数の関数です。

上記の伝達関数の導出については、後の章で説明します。

フィードバックの効果

フィードバックの効果を理解しましょう。

全体的なゲインに対するフィードバックの影響

• 式2から、負帰還閉ループ制御システムの全体的なゲインは、「G」と（1 + GH）の比率であると言えます。したがって、（1 + GH）の値に応じて、全体的なゲインが増減する場合があります。

• （1 + GH）の値が1未満の場合、全体的なゲインが増加します。この場合、フィードバックパスのゲインが負であるため、「GH」値は負になります。

• （1 + GH）の値が1より大きい場合、全体的なゲインは減少します。この場合、フィードバックパスのゲインが正であるため、「GH」値は正です。

一般に、「G」と「H」は周波数の関数です。したがって、フィードバックにより、一方の周波数範囲でシステムの全体的なゲインが増加し、もう一方の周波数範囲で減少します。

感度に対するフィードバックの影響

Sensitivity 負帰還閉ループ制御システムの全体的なゲインのT）開ループゲインの変動（G） と定義されている

$S_{G}^{T} = \frac{\frac{\partial T}{T}}{\frac{\partial G}{G}}=\frac{Percentage\: change \: in \:T}{Percentage\: change \: in \:G}$ （式3）

どこ、 ∂T Gの増分変化によるTの増分変化です。

式3を次のように書き直すことができます。

$S_{G}^{T}=\frac{\partial T}{\partial G}\frac{G}{T}$ （式4）

式2の両側でGに関して偏微分を行います。

$\frac{\partial T}{\partial G}=\frac{\partial}{\partial G}\left (\frac{G}{1+GH} \right )=\frac{(1+GH).1-G(H)}{(1+GH)^2}=\frac{1}{(1+GH)^2}$ （式5）

式2から、次のようになります。

$\frac{G}{T}=1+GH$ （式6）

式4に式5と式6を代入します。

$$S_{G}^{T}=\frac{1}{(1+GH)^2}(1+GH)=\frac{1}{1+GH}$$

だから、私たちは sensitivity（1 + GH）の逆数としての閉ループ制御システムの全体的なゲインの。したがって、感度は（1 + GH）の値に応じて増減する場合があります。

• （1 + GH）の値が1未満の場合、感度が高くなります。この場合、フィードバックパスのゲインが負であるため、「GH」値は負です。

• （1 + GH）の値が1より大きい場合、感度は低下します。この場合、フィードバックパスのゲインが正であるため、「GH」値は正です。

一般に、「G」と「H」は周波数の関数です。したがって、フィードバックは、一方の周波数範囲でシステムゲインの感度を上げ、もう一方の周波数範囲で下げます。したがって、システムがパラメータの変動に鈍感または鈍感になるように、「GH」の値を選択する必要があります。

安定性に対するフィードバックの影響

• 出力が制御されている場合、システムは安定していると言われます。そうでなければ、それは不安定であると言われます。

• 式2では、分母の値がゼロ（つまり、GH = -1）の場合、制御システムの出力は無限大になります。そのため、制御システムが不安定になります。

したがって、制御システムを安定させるためには、フィードバックを適切に選択する必要があります。

フィードバックがノイズに及ぼす影響

フィードバックがノイズに与える影響を知るために、ノイズ信号のみによるフィードバックがある場合とない場合の伝達関数の関係を比較してみましょう。

考えてみてください open loop control system 以下に示すようなノイズ信号で。

ザ・ open loop transfer function ノイズ信号だけで

$\frac{C(s)}{N(s)}=G_b$ （式7）

他の入力を行うことで得られます $R(s)$ ゼロに等しい。

考えてみてください closed loop control system 以下に示すようなノイズ信号で。

ザ・ closed loop transfer function ノイズ信号だけで

$\frac{C(s)}{N(s)}=\frac{G_b}{1+G_aG_bH}$ （式8）

他の入力を行うことで得られます $R(s)$ ゼロに等しい。

式7と式8を比較してください

閉ループ制御システムでは、ノイズ信号によるゲインが1分の1に減少します。 $(1+G_a G_b H)$ ただし、 $(1+G_a G_b H)$ 1より大きい。

制御システムは、次のような一連の数式で表すことができます。 mathematical model。これらのモデルは、制御システムの分析と設計に役立ちます。制御システムの分析とは、入力と数学的モデルがわかっているときに出力を見つけることを意味します。制御システムの設計とは、入力と出力がわかっているときに数学モデルを見つけることを意味します。

以下の数学モデルが主に使用されます。

• 微分方程式モデル
• 伝達関数モデル
• 状態空間モデル

この章の最初の2つのモデルについて説明します。

微分方程式モデル

微分方程式モデルは、制御システムの時間領域の数学モデルです。微分方程式モデルについては、次の手順に従ってください。

• 与えられた制御システムに基本法を適用します。

• 中間変数を削除して、入力と出力に関する微分方程式を取得します。

例

次の図に示すように、次の電気システムについて考えてみます。この回路は、抵抗、インダクタ、コンデンサで構成されています。これらすべての電気要素はで接続されていますseries。この回路に印加される入力電圧は$v_i$ コンデンサ両端の電圧は出力電圧です $v_o$。

この回路のメッシュ方程式は次のとおりです。

$$v_i=Ri+L\frac{\text{d}i}{\text{d}t}+v_o$$

代用、コンデンサを流れる電流 $i=c\frac{\text{d}v_o}{\text{d}t}$ 上記の式で。

$$\Rightarrow\:v_i=RC\frac{\text{d}v_o}{\text{d}t}+LC\frac{\text{d}^2v_o}{\text{d}t^2}+v_o$$

$$\Rightarrow\frac{\text{d}^2v_o}{\text{d}t^2}+\left ( \frac{R}{L} \right )\frac{\text{d}v_o}{\text{d}t}+\left ( \frac{1}{LC} \right )v_o=\left ( \frac{1}{LC} \right )v_i$$

上記の式は2次です differential equation。

伝達関数モデル

伝達関数モデルは、制御システムのsドメイン数学モデルです。ザ・Transfer function 線形時不変（LTI）システムのは、すべての初期条件がゼロであると仮定して、出力のラプラス変換と入力のラプラス変換の比率として定義されます。

場合 $x(t)$ そして $y(t)$ はLTIシステムの入力と出力であり、対応するラプラス変換は次のようになります。 $X(s)$ そして $Y(s)$。

したがって、LTIシステムの伝達関数は次の比率に等しくなります。 $Y(s)$ そして $X(s)$。

$$i.e.,\: Transfer\: Function =\frac{Y(s)}{X(s)}$$

LTIシステムの伝達関数モデルを次の図に示します。

ここでは、伝達関数を内部に持つブロックを備えたLTIシステムを表現しました。そして、このブロックには入力があります$X(s)$ ＆出力 $Y(s)$。

例

以前は、電気システムの微分方程式は次のようになりました。

$$\frac{\text{d}^2v_o}{\text{d}t^2}+\left ( \frac{R}{L} \right )\frac{\text{d}v_o}{\text{d}t}+\left ( \frac{1}{LC} \right )v_o=\left ( \frac{1}{LC} \right )v_i$$

両側にラプラス変換を適用します。

$$s^2V_o(s)+\left ( \frac{sR}{L} \right )V_o(s)+\left ( \frac{1}{LC} \right )V_o(s)=\left ( \frac{1}{LC} \right )V_i(s)$$

$$\Rightarrow \left \{ s^2+\left ( \frac{R}{L} \right )s+\frac{1}{LC} \right \}V_o(s)=\left ( \frac{1}{LC} \right )V_i(s)$$

$$\Rightarrow \frac{V_o(s)}{V_i(s)}=\frac{\frac{1}{LC}}{s^2+\left ( \frac{R}{L} \right )s+\frac{1}{LC}}$$

どこ、

• $v_i(s)$ 入力電圧のラプラス変換です $v_i$

• $v_o(s)$ 出力電圧のラプラス変換です $v_o$

上記の式は transfer function二次電気システムの。このシステムの伝達関数モデルを以下に示します。

ここでは、内部に伝達関数を持つブロックを備えた2次電気システムを示します。そして、このブロックには入力があります$V_i(s)$ ＆出力 $V_o(s)$。

この章では、 differential equation modeling機械システムの。モーションのタイプに基づいて、2つのタイプの機械システムがあります。

• 並進機械システム
• 回転機械システム

並進機械システムのモデリング

並進機械システムは、 straight line。これらのシステムは、主に3つの基本要素で構成されています。それらは、マス、スプリング、ダッシュポットまたはダンパーです。

並進機械システムに力が加えられると、システムの質量、弾性、摩擦による反対の力に対抗します。加えられた力と反対の力は反対方向にあるため、システムに作用する力の代数和はゼロです。ここで、これら3つの要素が個別に対抗する力を見てみましょう。

質量

質量は体の特性であり、 kinetic energy。質量のある物体に力が加わった場合M、それからそれは質量による反対の力によって反対されます。この反対の力は、体の加速度に比例します。弾性と摩擦は無視できると仮定します。

$$F_m\propto\: a$$

$$\Rightarrow F_m=Ma=M\frac{\text{d}^2x}{\text{d}t^2}$$

$$F=F_m=M\frac{\text{d}^2x}{\text{d}t^2}$$

どこ、

• F 加えられる力です

• F_m 質量による反対の力です

• M 質量です

• a 加速です

• x 変位です

春

春は要素であり、 potential energy。ばねに力が加わった場合K、それからそれはばねの弾性による反対の力によって反対されます。この反対の力は、ばねの変位に比例します。質量と摩擦はごくわずかであると仮定します。

$$F\propto\: x$$

$$\Rightarrow F_k=Kx$$

$$F=F_k=Kx$$

どこ、

• F 加えられる力です

• F_k ばねの弾性による反対の力です

• K ばね定数です

• x 変位です

ダッシュポット

ダッシュポットに力が加えられた場合 B、それからそれはのために反対の力によって反対されます frictionダッシュポットの。この反対の力は、体の速度に比例します。質量と弾性は無視できると仮定します。

$$F_b\propto\: \nu$$

$$\Rightarrow F_b=B\nu=B\frac{\text{d}x}{\text{d}t}$$

$$F=F_b=B\frac{\text{d}x}{\text{d}t}$$

どこ、

• F_b ダッシュポットの摩擦による反対の力です

• B は摩擦係数です

• v 速度です

• x 変位です

回転機械システムのモデリング

回転機械システムは、固定軸を中心に移動します。これらのシステムは、主に3つの基本要素で構成されています。それらはmoment of inertia, torsional spring そして dashpot。

回転機械システムにトルクが加えられると、システムの慣性モーメント、弾性、摩擦により、反対のトルクが発生します。加えられたトルクと反対のトルクは反​​対方向であるため、システムに作用するトルクの代数和はゼロです。ここで、これら3つの要素が個別に対抗するトルクを見てみましょう。

慣性モーメント

並進機械システムでは、質量は運動エネルギーを蓄えます。同様に、回転機械システムでは、慣性モーメントが保存されますkinetic energy。

慣性モーメントのある物体にトルクを加えた場合 J、次に、慣性モーメントによる反対のトルクが反対になります。この反対のトルクは、物体の角加速度に比例します。弾性と摩擦は無視できると仮定します。

$$T_j\propto\: \alpha$$

$$\Rightarrow T_j=J\alpha=J\frac{\text{d}^2\theta}{\text{d}t^2}$$

$$T=T_j=J\frac{\text{d}^2\theta}{\text{d}t^2}$$

どこ、

• T 加えられるトルクです

• T_j は慣性モーメントによる逆トルクです

• J 慣性モーメントです

• α 角加速度です

• θ 角変位です

ねじりばね

並進機械システムでは、ばねは位置エネルギーを蓄えます。同様に、回転機械システムでは、ねじりばねはpotential energy。

ねじりばねにトルクがかかる場合 K、次に、ねじりばねの弾性による反対のトルクによって反対されます。この反対のトルクは、ねじりばねの角変位に比例します。慣性モーメントと摩擦は無視できると仮定します。

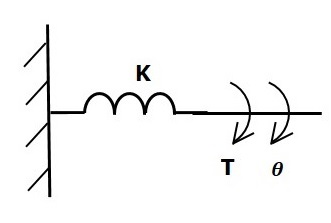
$$T_k\propto\: \theta$$

$$\Rightarrow T_k=K\theta$$

$$T=T_k=K\theta$$

どこ、

• T 加えられるトルクです

• T_k ねじりばねの弾性による反対のトルクです

• K ねじりばね定数です

• θ 角変位です

ダッシュポット

ダッシュポットにトルクがかかっている場合 B、それからそれは反対のトルクによって反対されます rotational frictionダッシュポットの。この反対のトルクは、物体の角速度に比例します。慣性モーメントと弾性は無視できると仮定します。

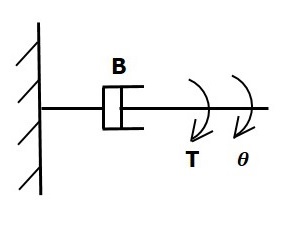
$$T_b\propto\: \omega$$

$$\Rightarrow T_b=B\omega=B\frac{\text{d}\theta}{\text{d}t}$$

$$T=T_b=B\frac{\text{d}\theta}{\text{d}t}$$

どこ、

• T_b ダッシュポットの回転摩擦による反対のトルクです

• B は回転摩擦係数です

• ω 角速度です

• θ 角変位です

2つのシステムは analogous 次の2つの条件が満たされている場合は相互に。

• 2つのシステムは物理的に異なります
• これら2つのシステムの微分方程式モデリングは同じです

電気システムと機械システムは、物理的に異なる2つのシステムです。並進機械システムの電気的アナロジーには2つのタイプがあります。それらは力電圧のアナロジーと力電流のアナロジーです。

力の電圧のアナロジー

力の電圧のアナロジーでは、の数式 translational mechanical system 電気システムのメッシュ方程式と比較されます。

次の図に示すように、次の並進機械システムについて考えてみます。

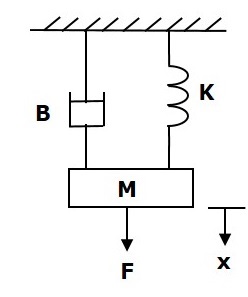
ザ・ force balanced equation このシステムの

$$F=F_m+F_b+F_k$$

$\Rightarrow F=M\frac{\text{d}^2x}{\text{d}t^2}+B\frac{\text{d}x}{\text{d}t}+Kx$ (Equation 1)

次の図に示すように、次の電気システムについて考えてみます。この回路は、抵抗、インダクタ、コンデンサで構成されています。これらの電気素子はすべて直列に接続されています。この回路に印加される入力電圧は$V$ ボルトと回路を流れる電流は $i$ アンペア。

この回路のメッシュ方程式は次のとおりです。

$V=Ri+L\frac{\text{d}i}{\text{d}t}+\frac{1}{c}\int idt$ (Equation 2)

代替、 $i=\frac{\text{d}q}{\text{d}t}$ 式2で。

$$V=R\frac{\text{d}q}{\text{d}t}+L\frac{\text{d}^2q}{\text{d}t^2}+\frac{q}{C}$$

$\Rightarrow V=L\frac{\text{d}^2q}{\text{d}t^2}+R\frac{\text{d}q}{\text{d}t}+\left ( \frac{1}{c} \right )q$ (Equation 3)

式1と式3を比較することにより、並進機械システムと電気システムの類似した量が得られます。次の表は、これらの類似した数量を示しています。

並進機械システム	電気システム
Force（F）	電圧（V）
質量（M）	インダクタンス（L）
摩擦係数（B）	抵抗（R）
ばね定数（K）	静電容量の逆数 $(\frac{1}{c})$
変位（x）	Charge（q）
速度（v）	Current（i）

同様に、回転機械システムにはトルク電圧のアナロジーがあります。ここで、このアナロジーについて説明しましょう。

トルク電圧のアナロジー

この例えでは、の数式は rotational mechanical system 電気システムのメッシュ方程式と比較されます。

回転機械システムを次の図に示します。

トルクバランス方程式は

$$T=T_j+T_b+T_k$$

$\Rightarrow T=J\frac{\text{d}^2\theta}{\text{d}t^2}+B\frac{\text{d}\theta}{\text{d}t}+k\theta$ (Equation 4)

式4と式3を比較することにより、回転機械システムと電気システムの類似した量が得られます。次の表は、これらの類似した数量を示しています。

回転機械システム	電気システム
トルク（T）	電圧（V）
慣性モーメント（J）	インダクタンス（L）
回転摩擦係数（B）	抵抗（R）
ねじりばね定数（K）	静電容量の逆数 $(\frac{1}{c})$
角変位（θ）	Charge（q）
角速度（ω）	Current（i）

力の現在のアナロジー

力の電流のアナロジーでは、の数式 translational mechanical system 電気系統の節点方程式と比較されます。

次の図に示すように、次の電気システムについて考えてみます。この回路は、電流源、抵抗、インダクタ、コンデンサで構成されています。これらの電気素子はすべて並列に接続されています。

節点方程式は

$i=\frac{V}{R}+\frac{1}{L}\int Vdt+C\frac{\text{d}V}{\text{d}t}$ (Equation 5)

代替、 $V=\frac{\text{d}\Psi}{\text{d}t}$ 式5で。

$$i=\frac{1}{R}\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi+C\frac{\text{d}^2\Psi}{\text{d}t^2}$$

$\Rightarrow i=C\frac{\text{d}^2\Psi}{\text{d}t^2}+\left ( \frac{1}{R} \right )\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi$ (Equation 6)

式1と式6を比較することにより、並進機械システムと電気システムの類似した量が得られます。次の表は、これらの類似した数量を示しています。

並進機械システム	電気システム
Force（F）	Current（i）
質量（M）	静電容量（C）
摩擦係数（B）	抵抗の逆数$(\frac{1}{R})$
ばね定数（K）	インダクタンスの逆数$(\frac{1}{L})$
変位（x）	磁束（ψ）
速度（v）	電圧（V）

同様に、回転機械システムにはトルク電流のアナロジーがあります。ここで、このアナロジーについて説明しましょう。

トルク電流のアナロジー

このアナロジーでは、の数式 rotational mechanical system 電気システムの節点メッシュ方程式と比較されます。

式4と式6を比較することにより、回転機械システムと電気システムの類似した量が得られます。次の表は、これらの類似した数量を示しています。

回転機械システム	電気システム
トルク（T）	Current（i）
慣性モーメント（J）	静電容量（C）
回転摩擦係数（B）	抵抗の逆数$(\frac{1}{R})$
ねじりばね定数（K）	インダクタンスの逆数$(\frac{1}{L})$
角変位（θ）	磁束（ψ）
角速度（ω）	電圧（V）

この章では、機械システムの電気的アナロジーについて説明しました。これらのアナロジーは、類似の電気システムから機械システムのような非電気システムを研究および分析するのに役立ちます。

ブロックダイアグラムは、単一のブロックまたはブロックの組み合わせで構成されます。これらは、制御システムを図で表すために使用されます。

ブロック図の基本要素

ブロックダイアグラムの基本要素は、ブロック、加算ポイント、およびテイクオフポイントです。これらの要素を特定するために、次の図に示すような閉ループ制御システムのブロック図を考えてみましょう。

上記のブロック図は、伝達関数G（s）とH（s）を持つ2つのブロックで構成されています。また、1つの加算ポイントと1つの離陸ポイントがあります。矢印は信号の流れの方向を示します。これらの要素を1つずつ説明していきましょう。

ブロック

コンポーネントの伝達関数はブロックで表されます。ブロックには単一の入力と単一の出力があります。

次の図は、入力X（s）、出力Y（s）、および伝達関数G（s）を持つブロックを示しています。

伝達関数、$G(s)=\frac{Y(s)}{X(s)}$

$$\Rightarrow Y(s)=G(s)X(s)$$

ブロックの出力は、ブロックの伝達関数に入力を掛けることによって得られます。

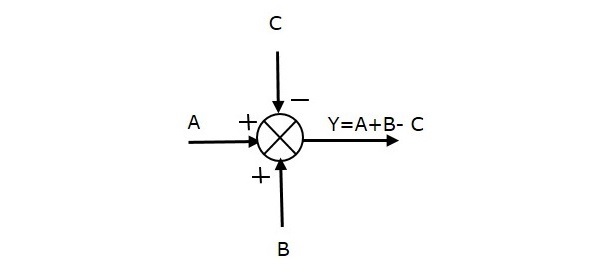
加算点

加算点は、内部に十字（X）が付いた円で表されます。2つ以上の入力と1つの出力があります。入力の代数和を生成します。また、入力の極性に基づいて、入力の合計または減算、あるいは合計と減算の組み合わせを実行します。これらの3つの操作を1つずつ見ていきましょう。

次の図は、2つの入力（A、B）と1つの出力（Y）の合計点を示しています。ここで、入力AとBは正の符号を持っています。したがって、加算点は出力Yを生成します。sum of A and B.

つまり、Y = A + Bです。

次の図は、2つの入力（A、B）と1つの出力（Y）の合計点を示しています。ここで、入力AとBは反対の符号を持っています。つまり、Aは正の符号を持ち、Bは負の符号を持っています。したがって、加算点は出力を生成しますY として difference of A and B。

Y = A +（-B）= A--B。

次の図は、3つの入力（A、B、C）と1つの出力（Y）の合計点を示しています。ここで、入力AとBは正の符号を持ち、Cは負の符号を持っています。したがって、加算点は出力を生成しますY なので

Y = A + B +（− C）= A + B −C。

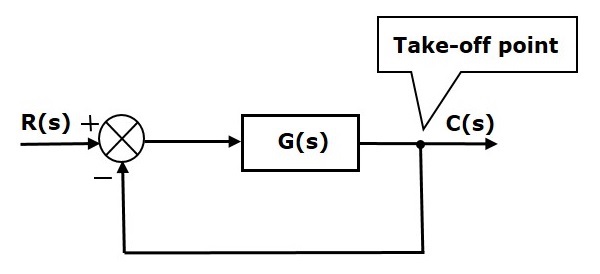
離陸地点

テイクオフポイントは、同じ入力信号が複数のブランチを通過できるポイントです。つまり、テイクオフポイントを使用して、同じ入力を1つ以上のブロックに適用し、ポイントを合計することができます。

次の図では、テイクオフポイントを使用して、同じ入力R（s）をさらに2つのブロックに接続しています。

次の図では、テイクオフポイントを使用して、入力の1つとして出力C（s）を加算ポイントに接続しています。

電気システムのブロック図表現

このセクションでは、電気システムをブロック図で表現しましょう。電気システムには、主に3つの基本要素が含まれています—resistor, inductor and capacitor。

次の図に示すような一連のRLC回路について考えてみます。ここで、V _i（t）とV _o（t）は入力電圧と出力電圧です。i（t）を回路を流れる電流とします。この回路は時間領域にあります。

この回路にラプラス変換を適用することにより、回路はsドメインになります。回路は次の図のようになります。

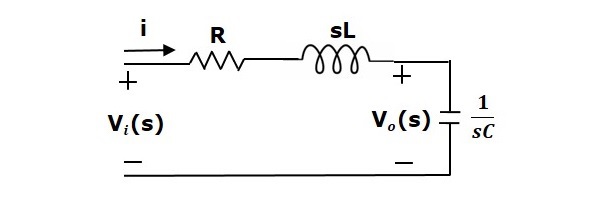
上記の回路から、次のように書くことができます。

$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$

$\Rightarrow I(s)=\left \{ \frac{1}{R+sL} \right \}\left \{ V_i(s)-V_o(s) \right \}$ (Equation 1)

$V_o(s)=\left ( \frac{1}{sC} \right )I(s)$ (Equation 2)

ここで、これら2つの方程式のブロック図を個別に描画してみましょう。次に、これらのブロック図を適切に組み合わせて、一連のRLC回路（sドメイン）の全体的なブロック図を取得します。

式1は、伝達関数を持つブロックを使用して実装できます。 $\frac{1}{R+sL}$。このブロックの入力と出力は次のとおりです。$\left \{ V_i(s)-V_o(s) \right \}$ そして $I(s)$。取得するには合計ポイントが必要です$\left \{ V_i(s)-V_o(s) \right \}$。式1のブロック図を次の図に示します。

式2は、伝達関数を持つブロックを使用して実装できます。 $\frac{1}{sC}$。このブロックの入力と出力は次のとおりです。$I(s)$ そして $V_o(s)$。式2のブロック図を次の図に示します。

次の図に、一連のRLC回路（sドメイン）の全体的なブロック図を示します。

同様に、あなたは描くことができます block diagram この簡単な手順に従うだけで、電気回路やシステムの

• ラプラス変換を適用して、時間領域の電気回路をs領域の電気回路に変換します。

• すべての直列分岐要素を流れる電流とすべてのシャント分岐にかかる電圧の式を書き留めます。

• 上記のすべての方程式のブロック図を個別に描画します。

• これらすべてのブロック図を適切に組み合わせて、電気回路（sドメイン）の全体的なブロック図を取得します。

ブロック図代数は、ブロック図の基本要素に関係する代数に他なりません。この代数は、代数方程式の絵画的表現を扱います。

ブロックの基本的な接続

2つのブロック間の接続には3つの基本的なタイプがあります。

直列接続

直列接続は、 cascade connection。次の図では、伝達関数を持つ2つのブロック$G_1(s)$ そして $G_2(s)$ 直列に接続されています。

この組み合わせの場合、出力が得られます $Y(s)$ なので

$$Y(s)=G_2(s)Z(s)$$

どこ、 $Z(s)=G_1(s)X(s)$

$$\Rightarrow Y(s)=G_2(s)[G_1(s)X(s)]=G_1(s)G_2(s)X(s)$$

$$\Rightarrow Y(s)=\lbrace G_1(s)G_2(s)\rbrace X(s)$$

この方程式を出力方程式の標準形式と比較します。 $Y(s)=G(s)X(s)$。どこ、$G(s) = G_1(s)G_2(s)$。

つまり、 series connection1つのブロックで2つのブロックの。この単一ブロックの伝達関数はproduct of the transfer functionsそれらの2つのブロックの。同等のブロック図を以下に示します。

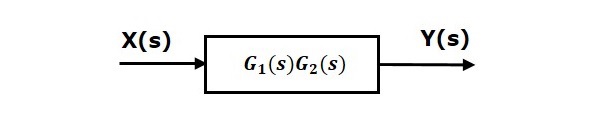
同様に、「n」ブロックの直列接続を単一のブロックで表すことができます。この単一ブロックの伝達関数は、これらすべての「n」ブロックの伝達関数の積です。

並列接続

で接続されているブロック parallel があります same input。次の図では、伝達関数を持つ2つのブロック$G_1(s)$ そして $G_2(s)$並列に接続されています。これら2つのブロックの出力は、加算点に接続されます。

この組み合わせの場合、出力が得られます $Y(s)$ なので

$$Y(s)=Y_1(s)+Y_2(s)$$

どこ、 $Y_1(s)=G_1(s)X(s)$ そして $Y_2(s)=G_2(s)X(s)$

$$\Rightarrow Y(s)=G_1(s)X(s)+G_2(s)X(s)=\lbrace G_1(s)+G_2(s)\rbrace X(s)$$

この方程式を出力方程式の標準形式と比較します。 $Y(s)=G(s)X(s)$。

どこ、 $G(s)=G_1(s)+G_2(s)$。

つまり、 parallel connection1つのブロックで2つのブロックの。この単一ブロックの伝達関数はsum of the transfer functionsそれらの2つのブロックの。同等のブロック図を以下に示します。

同様に、「n」ブロックの並列接続を単一のブロックで表すことができます。この単一ブロックの伝達関数は、これらすべての「n」ブロックの伝達関数の代数和です。

フィードバック接続

前の章で説明したように、2つのタイプがあります feedback—正のフィードバックと負のフィードバック。次の図は、負帰還制御システムを示しています。ここでは、伝達関数を持つ2つのブロック$G(s)$ そして $H(s)$ 閉ループを形成します。

加算点の出力は-

$$E(s)=X(s)-H(s)Y(s)$$

出力 $Y(s)$ は-

$$Y(s)=E(s)G(s)$$

代替 $E(s)$ 上記の式の値。

$$Y(s)=\left \{ X(s)-H(s)Y(s)\rbrace G(s) \right\}$$

$$Y(s)\left \{ 1+G(s)H(s)\rbrace = X(s)G(s) \right\}$$

$$\Rightarrow \frac{Y(s)}{X(s)}=\frac{G(s)}{1+G(s)H(s)}$$

したがって、負帰還閉ループ伝達関数は次のようになります。 $\frac{G(s)}{1+G(s)H(s)}$

これは、2つのブロックの負のフィードバック接続を1つのブロックで表すことができることを意味します。この単一ブロックの伝達関数は、負帰還の閉ループ伝達関数です。同等のブロック図を以下に示します。

同様に、1つのブロックで2つのブロックの正のフィードバック接続を表すことができます。この単一ブロックの伝達関数は、正のフィードバックの閉ループ伝達関数です。$\frac{G(s)}{1-G(s)H(s)}$

ポイントを合計するためのブロック図代数

ブロックに関して加算点をシフトする可能性は2つあります-

• ブロック後の合計ポイントのシフト
• ブロックの前の合計ポイントのシフト

ここで、上記の2つのケースでどのような調整を行う必要があるかを1つずつ見ていきましょう。

ブロック後の合計ポイントのシフト

次の図に示すブロック図について考えてみます。ここでは、加算点はブロックの前にあります。

加算点には2つの入力があります $R(s)$ そして $X(s)$。その出力は$\left \{R(s)+X(s)\right\}$。

したがって、ブロックへの入力 $G(s)$ です $\left \{R(s)+X(s)\right \}$ そしてそれの出力は–

$$Y(s)=G(s)\left \{R(s)+X(s)\right \}$$

$\Rightarrow Y(s)=G(s)R(s)+G(s)X(s)$ (Equation 1)

ここで、合計ポイントをブロックの後にシフトします。このブロック図を次の図に示します。

ブロックの出力 $G(s)$ です $G(s)R(s)$。

加算点の出力は次のとおりです。

$Y(s)=G(s)R(s)+X(s)$ (Equation 2)

式1と式2を比較してください。

第一期 $‘G(s) R(s)’$両方の方程式で同じです。ただし、第2期には違いがあります。第2項も同じにするために、もう1つのブロックが必要です$G(s)$。入力があります$X(s)$ このブロックの出力は、代わりに加算点への入力として与えられます $X(s)$。このブロック図を次の図に示します。

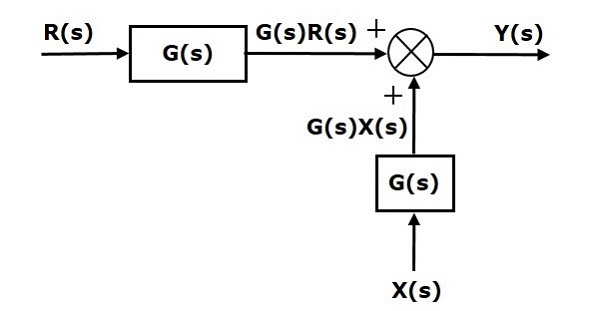
ブロック前の加算点のシフト

次の図に示すブロック図について考えてみます。ここでは、加算点はブロックの後にあります。

このブロック図の出力は-

$Y(s)=G(s)R(s)+X(s)$ (Equation 3)

ここで、合計ポイントをブロックの前にシフトします。このブロック図を次の図に示します。

このブロック図の出力は-

$Y(S)=G(s)R(s)+G(s)X(s)$ (Equation 4)

式3と式4を比較してください。

第一期 $‘G(s) R(s)’$両方の方程式で同じです。ただし、第2期には違いがあります。第2項も同じにするために、もう1つのブロックが必要です$\frac{1}{G(s)}$。入力があります$X(s)$ このブロックの出力は、代わりに加算点への入力として与えられます $X(s)$。このブロック図を次の図に示します。

離陸地点のブロック図代数

ブロックに関してテイクオフポイントをシフトする可能性は2つあります-

• ブロック後の離陸地点のシフト
• ブロック前の離陸地点の移動

ここで、上記の2つのケースでどのような取り決めが行われるのかを1つずつ見ていきましょう。

ブロック後の離陸地点のシフト

次の図に示すブロック図について考えてみます。この場合、離陸地点はブロックの前にあります。

ここに、 $X(s)=R(s)$ そして $Y(s)=G(s)R(s)$

ブロックの後に離陸ポイントをシフトすると、出力 $Y(s)$同じになります。しかし、違いがあります$X(s)$値。だから、同じを得るために$X(s)$ 値、もう1つのブロックが必要です $\frac{1}{G(s)}$。入力があります$Y(s)$ そして出力は $X(s)$。このブロック図を次の図に示します。

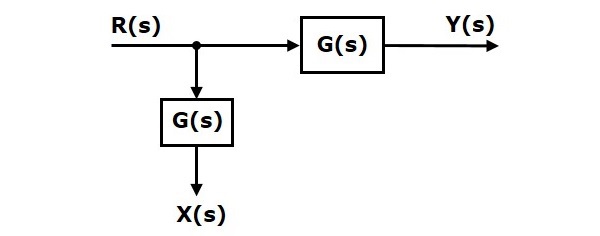
ブロック前の離陸地点の移動

次の図に示すブロック図について考えてみます。ここでは、離陸地点はブロックの後にあります。

ここに、 $X(s)=Y(s)=G(s)R(s)$

ブロックの前でテイクオフポイントをシフトすると、出力 $Y(s)$同じになります。しかし、違いがあります$X(s)$値。だから、同じになるために$X(s)$ 値、もう1つのブロックが必要です $G(s)$。入力があります$R(s)$ そして出力は $X(s)$。このブロック図を次の図に示します。

前の章で説明した概念は、ブロック図を削減（簡略化）するのに役立ちます。

ブロック図の削減ルール

これらのルールに従って、多くのブロック、合計ポイント、およびテイクオフポイントを含むブロックダイアグラムを簡略化（縮小）します。

• Rule 1 −直列に接続されているブロックを確認し、単純化します。

• Rule 2 −並列に接続されているブロックを確認し、単純化します。

• Rule 3 −フィードバックループで接続されているブロックを確認し、単純化します。

• Rule 4 −単純化しながら離陸地点に問題がある場合は、右にシフトします。

• Rule 5 −単純化しながらポイントを合計するのが難しい場合は、左にシフトします。

• Rule 6 −簡略化されたフォーム、つまり単一ブロックが得られるまで、上記の手順を繰り返します。

Note −この単一ブロックに存在する伝達関数は、ブロック図全体の伝達関数です。

例

次の図に示すブロック図について考えてみます。ブロック線図縮小規則を使用して、このブロック線図を簡略化（縮小）しましょう。

Step 1 −ブロックにはルール1を使用する $G_1$ そして $G_2$。ブロックにはルール2を使用する$G_3$ そして $G_4$。変更されたブロック図を次の図に示します。

Step 2 −ブロックにはルール3を使用する $G_1G_2$ そして $H_1$。ブロック後に離陸地点を移動するには、ルール4を使用します$G_5$。変更されたブロック図を次の図に示します。

Step 3 −ブロックにはルール1を使用する $(G_3 + G_4)$ そして $G_5$。変更されたブロック図を次の図に示します。

Step 4 −ブロックにはルール3を使用する $(G_3 + G_4)G_5$ そして $H_3$。変更されたブロック図を次の図に示します。

Step 5−直列に接続されたブロックにはルール1を使用します。変更されたブロック図を次の図に示します。

Step 6−フィードバックループで接続されたブロックにはルール3を使用します。変更されたブロック図を次の図に示します。これは簡略化されたブロック図です。

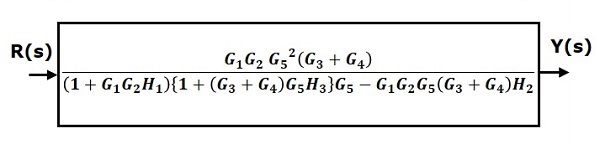
したがって、システムの伝達関数は次のようになります。

$$\frac{Y(s)}{R(s)}=\frac{G_1G_2G_5^2(G_3+G_4)}{(1+G_1G_2H_1)\lbrace 1+(G_3+G_4)G_5H_3\rbrace G_5-G_1G_2G_5(G_3+G_4)H_2}$$

Note −複数の入力を持つブロック線図の伝達関数を計算するには、次の手順に従います。

• Step 1 −一度に1つの入力を考慮してブロック図の伝達関数を見つけ、残りの入力をゼロにします。

• Step 2 −残りの入力に対して手順1を繰り返します。

• Step 3 −これらすべての伝達関数を追加して、全体的な伝達関数を取得します。

複雑なシステムでは、ブロック図の削減プロセスに時間がかかります。なぜなら、各ステップの後に（部分的に簡略化された）ブロック図を描く必要があるからです。したがって、この欠点を克服するには、シグナルフローグラフ（表現）を使用します。

次の2つの章では、信号フローグラフに関連する概念、つまり、特定のブロック図から信号フローグラフを表す方法と、削減プロセスを実行せずにゲイン式を使用するだけで伝達関数を計算する方法について説明します。

シグナルフローグラフは、代数方程式をグラフで表したものです。この章では、シグナルフローグラフに関連する基本的な概念について説明し、シグナルフローグラフの描画方法についても学習します。

シグナルフローグラフの基本要素

ノードとブランチは、シグナルフローグラフの基本要素です。

ノード

Node変数または信号のいずれかを表す点です。ノードには、入力ノード、出力ノード、混合ノードの3種類があります。

• Input Node −発信ブランチのみを持つノードです。

• Output Node −これは、着信ブランチのみを持つノードです。

• Mixed Node −これは、着信ブランチと発信ブランチの両方を持つノードです。

例

これらのノードを特定するために、次のシグナルフローグラフを検討してみましょう。

• ザ・ nodes このシグナルフローグラフに存在するのは y₁, y₂, y₃ そして y₄。

• y₁ そして y₄ は input node そして output node それぞれ。

• y₂ そして y₃ です mixed nodes。

ブランチ

Branch2つのノードを結合する線分です。それは両方を持っていますgain そして direction。たとえば、上記のシグナルフローグラフには4つのブランチがあります。これらのブランチにはgains の a, b, c そして -d。

シグナルフローグラフの構築

次の代数方程式を考慮して、シグナルフローグラフを作成しましょう。

$$y_2=a_{12}y_1+a_{42}y_4$$

$$y_3=a_{23}y_2+a_{53}y_5$$

$$y_4=a_{34}y_3$$

$$y_5=a_{45}y_4+a_{35}y_3$$

$$y_6=a_{56}y_5$$

6つあります nodes（Y ₁、Y ₂、Y ₃、Y ₄、Y ₅およびY ₆）、8branchesこのシグナルフローグラフでは。分岐の利得は、₁₂、₂₃、₃₄、₄₅、₅₆、₄₂、₅₃及び₃₅。

全体的なシグナルフローグラフを取得するには、各方程式のシグナルフローグラフを描画し、これらすべてのシグナルフローグラフを組み合わせて、以下の手順に従います。

Step 1 −のシグナルフローグラフ $y_2 = a_{13}y_1 + a_{42}y_4$ 次の図に示します。

Step 2 −のシグナルフローグラフ $y_3 = a_{23}y_2 + a_{53}y_5$ 次の図に示します。

Step 3 −のシグナルフローグラフ $y_4 = a_{34}y_3$ 次の図に示します。

Step 4 −のシグナルフローグラフ $y_5 = a_{45}y_4 + a_{35}y_3$ 次の図に示します。

Step 5 −のシグナルフローグラフ $y_6 = a_{56}y_5$ 次の図に示します。

Step 6 −システム全体のシグナルフローグラフを次の図に示します。

ブロック図のシグナルフローグラフへの変換

ブロックダイアグラムを同等のシグナルフローグラフに変換するには、次の手順に従います。

• ブロックダイアグラムのすべての信号、変数、合計ポイント、および離陸ポイントを次のように表します。 nodes シグナルフローグラフ。

• ブロック図のブロックを次のように表します branches シグナルフローグラフ。

• ブロック図のブロック内の伝達関数を次のように表します。 gains シグナルフローグラフの分岐の。

• ブロック図に従ってノードを接続します。2つのノード間に接続がある場合（ただし、間にブロックがない場合）、ブランチのゲインを1つとして表します。For example、加算点間、加算点と離陸点の間、入力と加算点の間、離陸点と出力の間。

例

次のブロック図を同等のシグナルフローグラフに変換してみましょう。

入力信号を表す $R(s)$ および出力信号 $C(s)$ 入力ノードとしてのブロック図の $R(s)$ および出力ノード $C(s)$ シグナルフローグラフの。

単に参考のために、残りのノード（Y ₁ Yに_{図9に示すように}）ブロック図に標識されます。入力ノードと出力ノード以外に9つのノードがあります。つまり、4つの合計ポイントに4つのノード、4つの離陸ポイントに4つのノード、ブロック間の変数に1つのノードです。$G_1$ そして $G_2$。

次の図は、同等のシグナルフローグラフを示しています。

メイソンのゲイン式（次の章で説明）を使用すると、このシグナルフローグラフの伝達関数を計算できます。これがシグナルフローグラフの利点です。ここでは、伝達関数を計算するためにシグナルフローグラフを単純化（縮小）する必要はありません。

メイソンのゲインフォーミュラについて説明しましょう。シグナルフローグラフに「N」個の順方向パスがあるとします。シグナルフローグラフの入力ノードと出力ノード間のゲインは、transfer functionシステムの。メイソンのゲイン式を使用して計算できます。

Mason’s gain formula is

$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^N _{i=1}P_i\Delta _i}{\Delta}$$

どこ、

• C(s) 出力ノードです

• R(s) 入力ノードです

• T 間の伝達関数またはゲインです $R(s)$ そして $C(s)$

• P_ii^番目のフォワードパスゲインです

$\Delta =1-(sum \: of \: all \: individual \: loop \: gains)$

$+(sum \: of \: gain \: products \: of \: all \: possible \: two \:nontouching \: loops)$

$$-(sum \: of \: gain \: products \: of \: all \: possible \: three \: nontouching \: loops)+...$$

Δ _iがIに触れているループ除去することによりΔから得られる^第フォワードパス。

ここに含まれる基本的な用語を理解するために、次のシグナルフローグラフを検討してください。

道

これは、あるノードから他のノードへの分岐矢印の方向への分岐の走査です。ノードを2回以上トラバースしないでください。

Examples − $y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5$ そして $y_5 \rightarrow y_3 \rightarrow y_2$

フォワードパス

入力ノードから出力ノードに存在するパスは、次のように知られています。 forward path。

Examples − $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ そして $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$。

フォワードパスゲイン

これは、フォワードパスのすべてのブランチゲインの積を計算することによって取得されます。

Examples − $abcde$ のフォワードパスゲインは $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ abgeはのフォワードパスゲインです $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$。

ループ

1つのノードから始まり、同じノードで終わるパスは、 loop。したがって、それは閉じたパスです。

Examples − $y_2 \rightarrow y_3 \rightarrow y_2$ そして $y_3 \rightarrow y_5 \rightarrow y_3$。

ループゲイン

これは、ループのすべての分岐ゲインの積を計算することによって得られます。

Examples − $b_j$ のループゲインは $y_2 \rightarrow y_3 \rightarrow y_2$ そして $g_h$ のループゲインは $y_3 \rightarrow y_5 \rightarrow y_3$。

非接触ループ

これらはループであり、共通ノードがあってはなりません。

Examples −ループ、 $y_2 \rightarrow y_3 \rightarrow y_2$ そして $y_4 \rightarrow y_5 \rightarrow y_4$ 触れないです。

メイソンのゲイン式を使用した伝達関数の計算

伝達関数を見つけるために同じシグナルフローグラフを考えてみましょう。

• フォワードパスの数、N = 2。

• 最初のフォワードパスは- $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$。

• 最初のフォワードパスゲイン、 $p_1 = abcde$。

• 2番目のフォワードパスは- $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$。

• 2番目のフォワードパスゲイン、 $p_2 = abge$。

• 個々のループの数、L = 5。

• ループは- $y_2 \rightarrow y_3 \rightarrow y_2$、 $y_3 \rightarrow y_5 \rightarrow y_3$、 $y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_3$、 $y_4 \rightarrow y_5 \rightarrow y_4$ そして $y_5 \rightarrow y_5$。

• ループゲインは- $l_1 = bj$、 $l_2 = gh$、 $l_3 = cdh$、 $l_4 = di$ そして $l_5 = f$。

• 2つの非接触ループの数= 2。

• 最初の非接触ループペアは- $y_2 \rightarrow y_3 \rightarrow y_2$、 $y_4 \rightarrow y_5 \rightarrow y_4$。

• 最初の非接触ループペアの積を得る、 $l_1l_4 = bjdi$

• 2番目の非接触ループペアは- $y_2 \rightarrow y_3 \rightarrow y_2$、 $y_5 \rightarrow y_5$。

• 2番目の非接触ループペアのゲイン積は- $l_1l_5 = bjf$

このシグナルフローグラフには、より多くの（2つ以上の）非接触ループは存在しません。

私たちは知っています、

$\Delta =1-(sum \: of \: all \: individual \: loop \: gains)$

$+(sum \: of \: gain \: products \: of \: all \: possible \: two \:nontouching \: loops)$

$$-(sum \: of \: gain \: products \: of \: all \: possible \: three \: nontouching \: loops)+...$$

上記の式の値を代入して、

$\Delta =1-(bj+gh+cdh+di+f)+(bjdi+bjf)-(0)$

$\Rightarrow \Delta=1-(bj+gh+cdh+di+f)+bjdi+bjf$

最初の順方向パスに触れないループはありません。

そう、 $\Delta_1=1$。

同様に、 $\Delta_2=1$。以来、2番目のフォワードパスに触れていないループはありません。

代用、メイソンのゲイン式でN = 2

$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^2 _{i=1}P_i\Delta _i}{\Delta}$$

$$T=\frac{C(s)}{R(s)}=\frac{P_1\Delta_1+P_2\Delta_2}{\Delta}$$

上記の式に必要なすべての値を代入します。

$$T=\frac{C(s)}{R(s)}=\frac{(abcde)1+(abge)1}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$

$$\Rightarrow T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$

したがって、伝達関数は-

$$T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$

時間領域と周波数領域の両方で制御システムの応答を分析できます。制御システムの周波数応答解析については、後の章で説明します。ここで、制御システムの時間応答解析について説明します。

時間応答とは何ですか？

入力に対する制御システムの出力が時間に対して変化する場合、それは time response制御システムの。時間応答は2つの部分で構成されます。

• 過渡応答
• 定常状態の応答

次の図に、時間領域での制御システムの応答を示します。

ここでは、過渡状態と定常状態の両方が図に示されています。これらの状態に対応する応答は、過渡状態および定常状態の応答として知られています。

数学的には、時間応答c（t）を次のように書くことができます。

$$c(t)=c_{tr}(t)+c_{ss}(t)$$

どこ、

• c _tr（t）は過渡応答です
• c _ss（t）は定常状態の応答です

過渡応答

制御システムに入力を適用した後、出力が定常状態に達するまでに一定の時間がかかります。したがって、出力は定常状態になるまで過渡状態になります。したがって、過渡状態中の制御システムの応答は、transient response。

't'の値が大きい場合、過渡応答はゼロになります。理想的には、この「t」の値は無限大であり、実際には5倍一定です。

数学的には、次のように書くことができます

$$\lim_{t\rightarrow \infty }c_{tr}(t)=0$$

定常状態の応答

「t」の値が大きい場合に過渡応答の値がゼロになった後も残る時間応答の部分は、次のように知られています。 steady state response。これは、定常状態の間でも過渡応答がゼロになることを意味します。

Example

制御システムの時間応答の過渡状態と定常状態の項を見つけましょう $c(t)=10+5e^{-t}$

ここで、第2期 $5e^{-t}$ としてゼロになります t無限大を示します。だから、これはtransient term。そして、最初の用語10はt無限に近づく。だから、これはsteady state term。

標準テスト信号

標準のテスト信号は、インパルス、ステップ、ランプ、放物線です。これらの信号は、出力の時間応答を使用して制御システムのパフォーマンスを知るために使用されます。

ユニットインパルス信号

単位インパルス信号δ（t）は次のように定義されます。

$\delta (t)=0$ にとって $t\neq 0$

そして $\int_{0^-}^{0^+} \delta (t)dt=1$

次の図は、単位インパルス信号を示しています。

したがって、単位インパルス信号は「t」がゼロに等しいときにのみ存在します。't'の周りの短い時間間隔でのこの信号の面積はゼロに等しくなります。単位インパルス信号の値は、他のすべての「t」の値ではゼロです。

ユニットステップ信号

単位ステップ信号u（t）は次のように定義されます。

$$u(t)=1;t\geq 0$$

$=0; t<0$

次の図は、ユニットステップ信号を示しています。

したがって、単位ステップ信号は、ゼロを含む「t」のすべての正の値に対して存在します。そして、その値はこの間隔の間1です。単位ステップ信号の値は、「t」のすべての負の値に対してゼロです。

ユニットランプ信号

ユニットランプ信号r（t）は次のように定義されます。

$$r(t)=t; t\geq 0$$

$=0; t<0$

ユニットランプ信号を書くことができます、 $r(t)$ 単位ステップ信号に関して、 $u(t)$ なので

$$r(t)=tu(t)$$

次の図は、ユニットランプ信号を示しています。

したがって、ユニットランプ信号は、ゼロを含む「t」のすべての正の値に対して存在します。そして、その値は、この間隔の間に「t」に関して直線的に増加します。単位ランプ信号の値は、「t」のすべての負の値に対してゼロです。

単位放物線信号

単位放物線信号p（t）は、次のように定義されます。

$$p(t)=\frac{t^2}{2}; t\geq 0$$

$=0; t<0$

単位放物線信号を書くことができます、 $p(t)$ 単位ステップ信号に関しては、 $u(t)$ なので、

$$p(t)=\frac{t^2}{2}u(t)$$

次の図は、単位放物線信号を示しています。

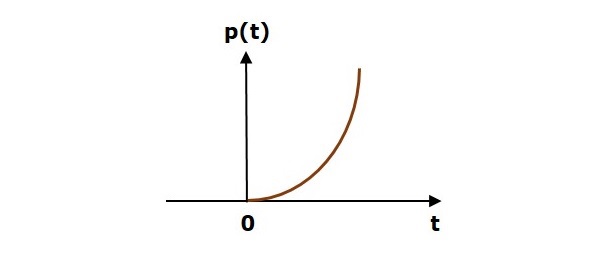
したがって、単位放物線信号は、のすべての正の値に対して存在します。 ‘t’ゼロを含む。そして、その値は、この間隔の間に「t」に関して非線形に増加します。単位放物線信号の値は、「t」のすべての負の値に対してゼロです。

この章では、一次システムの時間応答について説明します。次の閉ループ制御システムのブロック図を検討してください。ここでは、開ループ伝達関数、$\frac{1}{sT}$ ユニティネガティブフィードバックに接続されています。

閉ループ制御システムの伝達関数には、次のような単一の負のフィードバックがあることがわかっています。

$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$

代替、 $G(s)=\frac{1}{sT}$ 上記の式で。

$$\frac{C(s)}{R(s)}=\frac{\frac{1}{sT}}{1+\frac{1}{sT}}=\frac{1}{sT+1}$$

sの累乗は分母の項の1つです。したがって、上記の伝達関数は1次であり、システムは次のようになります。first order system。

上記の式を次のように書き直すことができます。

$$C(s)=\left ( \frac{1}{sT+1} \right )R(s)$$

どこ、

• C(s) は出力信号c（t）のラプラス変換です。

• R(s) は入力信号r（t）のラプラス変換であり、

• T は時定数です。

次の手順に従って、時間領域で1次システムの応答（出力）を取得します。

• 入力信号のラプラス変換を行います $r(t)$。

• 方程式を考えてみましょう。 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

• 代替 $R(s)$ 上記の式の値。

• の部分分数を行う $C(s)$ もし必要なら。

• 逆ラプラス変換をに適用する $C(s)$。

前の章では、インパルス、ステップ、ランプ、放物線などの標準的なテスト信号を見てきました。ここで、各入力に対する1次システムの応答を1つずつ調べてみましょう。応答の名前は、入力信号の名前に従って与えられます。たとえば、インパルス入力に対するシステムの応答は、インパルス応答と呼ばれます。

一次システムのインパルス応答

考えます unit impulse signal 一次システムへの入力として。

そう、 $r(t)=\delta (t)$

両側にラプラス変換を適用します。

$R(s)=1$

方程式を考えてみましょう。 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

代替、 $R(s) = 1$ 上記の式で。

$$C(s)=\left ( \frac{1}{sT+1} \right )(1)=\frac{1}{sT+1}$$

上記の方程式をラプラス変換の標準形式の1つに再配置します。

$$C(s)=\frac{1}{T\left (\ s+\frac{1}{T} \right )} \Rightarrow C(s)=\frac{1}{T}\left ( \frac{1}{s+\frac{1}{T}} \right )$$

両側に逆ラプラス変換を適用します。

$$c(t)=\frac{1}{T}e^\left ( {-\frac{t}{T}} \right )u(t)$$

単位インパルス応答を次の図に示します。

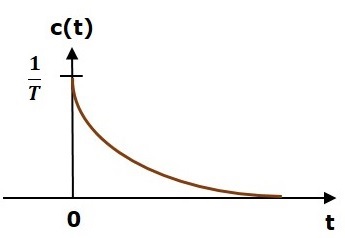
ザ・ unit impulse response、c（t）は、「t」の正の値の場合は指数関数的減衰信号であり、「t」の負の値の場合はゼロです。

一次システムのステップ応答

考えます unit step signal 一次システムへの入力として。

そう、 $r(t)=u(t)$

両側にラプラス変換を適用します。

$$R(s)=\frac{1}{s}$$

方程式を考えてみましょう。 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

代替、 $R(s)=\frac{1}{s}$ 上記の式で。

$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s} \right )=\frac{1}{s\left ( sT+1 \right )}$$

C（s）の部分分数を実行します。

$$C(s)=\frac{1}{s\left ( sT+1 \right )}=\frac{A}{s}+\frac{B}{sT+1}$$

$$\Rightarrow \frac{1}{s\left ( sT+1 \right )}=\frac{A\left ( sT+1 \right )+Bs}{s\left ( sT+1 \right )}$$

どちらの側でも、分母の項は同じです。だから、彼らはお互いにキャンセルされます。したがって、分子の項を等しくします。

$$1=A\left ( sT+1 \right )+Bs$$

両側の定数項を等しくすることにより、A = 1が得られます。

代入し、A = 1とし、の係数を等しくします。 s 両側の用語。

$$0=T+B \Rightarrow B=-T$$

の部分分数展開でA = 1およびB = −Tを代入します。 $C(s)$。

$$C(s)=\frac{1}{s}-\frac{T}{sT+1}=\frac{1}{s}-\frac{T}{T\left ( s+\frac{1}{T} \right )}$$

$$\Rightarrow C(s)=\frac{1}{s}-\frac{1}{s+\frac{1}{T}}$$

両側に逆ラプラス変換を適用します。

$$c(t)=\left ( 1-e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$

ザ・ unit step response、c（t）には、過渡状態と定常状態の両方の項があります。

単位ステップ応答の過渡項は-

$$c_{tr}(t)=-e^{-\left ( \frac{t}{T} \right )}u(t)$$

単位ステップ応答の定常状態の項は-

$$c_{ss}(t)=u(t)$$

次の図は、単位ステップ応答を示しています。

の値 unit step response, c(t)t = 0で、tのすべての負の値に対してゼロです。ゼロ値から徐々に増加し、最終的に定常状態で1に達します。したがって、定常状態の値は入力の大きさに依存します。

一次システムのランプ応答

考えます unit ramp signal 一次システムへの入力として。

$So, r(t)=tu(t)$

両側にラプラス変換を適用します。

$$R(s)=\frac{1}{s^2}$$

方程式を考えてみましょう。 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

代替、 $R(s)=\frac{1}{s^2}$ 上記の式で。

$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s^2} \right )=\frac{1}{s^2(sT+1)}$$

の部分分数を行う $C(s)$。

$$C(s)=\frac{1}{s^2(sT+1)}=\frac{A}{s^2}+\frac{B}{s}+\frac{C}{sT+1}$$

$$\Rightarrow \frac{1}{s^2(sT+1)}=\frac{A(sT+1)+Bs(sT+1)+Cs^2}{s^2(sT+1)}$$

どちらの側でも、分母の項は同じです。だから、彼らはお互いにキャンセルされます。したがって、分子の項を等しくします。

$$1=A(sT+1)+Bs(sT+1)+Cs^2$$

両側の定数項を等しくすることにより、A = 1が得られます。

A = 1に置き換えて、両側のs項の係数を等しくします。

$$0=T+B \Rightarrow B=-T$$

同様に、B = −Tを代入し、の係数を等しくします。 $s^2$両側の用語。あなたは得るでしょう$C=T^2$。

A = 1、B = −Tおよび $C = T^2$ の部分分数展開で $C(s)$。

$$C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{sT+1}=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{T\left ( s+\frac{1}{T} \right )}$$

$$\Rightarrow C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T}{s+\frac{1}{T}}$$

両側に逆ラプラス変換を適用します。

$$c(t)=\left ( t-T+Te^{-\left ( \frac{t}{T} \right )} \right )u(t)$$

ザ・ unit ramp response、c（t）には、過渡状態と定常状態の両方の項があります。

ユニットランプ応答の過渡項は-

$$c_{tr}(t)=Te^{-\left ( \frac{t}{T} \right )}u(t)$$

ユニットランプ応答の定常状態の項は-

$$c_{ss}(t)=(t-T)u(t)$$

次の図は、ユニットランプ応答を示しています。

ザ・ unit ramp response、c（t）は、tのすべての正の値に対してユニットランプ入力信号に従います。ただし、入力信号からT単位の偏差があります。

一次システムの放物線応答

考えます unit parabolic signal 一次システムへの入力として。

そう、 $r(t)=\frac{t^2}{2}u(t)$

両側にラプラス変換を適用します。

$$R(s)=\frac{1}{s^3}$$

方程式を考えてみましょう。 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

代替 $R(s)=\frac{1}{s^3}$ 上記の式で。

$$C(s)=\left ( \frac{1}{sT+1} \right )\left( \frac{1}{s^3} \right )=\frac{1}{s^3(sT+1)}$$

の部分分数を行う $C(s)$。

$$C(s)=\frac{1}{s^3(sT+1)}=\frac{A}{s^3}+\frac{B}{s^2}+\frac{C}{s}+\frac{D}{sT+1}$$

単純化すると、A、B、C、およびDの値が1になります。 $-T, \: T^2\: and \: −T^3$それぞれ。これらの値を上記のC（s）の部分分数展開に代入します。

$C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^3}{sT+1} \: \Rightarrow C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^2}{s+\frac{1}{T}}$

両側に逆ラプラス変換を適用します。

$$c(t)=\left ( \frac{t^2}{2} -Tt+T^2-T^2e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$

ザ・ unit parabolic response、c（t）には、過渡状態と定常状態の両方の項があります。

単位放物線応答の過渡項は次のとおりです。

$$C_{tr}(t)=-T^2e^{-\left ( \frac{t}{T} \right )}u(t)$$

単位放物線応答の定常状態項は次のとおりです。

$$C_{ss}(t)=\left ( \frac{t^2}{2} -Tt+T^2 \right )u(t)$$

これらの応答から、これらの応答は無限の時間でも増加し続けるため、一次制御システムはランプおよび放物線入力では安定していないと結論付けることができます。一次制御システムは、これらの応答が出力を制限しているため、インパルス入力とステップ入力で安定しています。ただし、インパルス応答には定常状態の項がありません。そのため、ステップ信号は、応答から制御システムを分析するために時間領域で広く使用されています。

この章では、2次システムの時間応答について説明します。次の閉ループ制御システムのブロック図を検討してください。ここでは、開ループ伝達関数、$\frac{\omega ^2_n}{s(s+2\delta \omega_n)}$ ユニティネガティブフィードバックに接続されています。

ユニティネガティブフィードバックを持つ閉ループ制御システムの伝達関数は、

$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$

代替、 $G(s)=\frac{\omega ^2_n}{s(s+2\delta \omega_n)}$ 上記の式で。

$$\frac{C(s)}{R(s)}=\frac{\left (\frac{\omega ^2_n}{s(s+2\delta \omega_n)} \right )}{1+ \left ( \frac{\omega ^2_n}{s(s+2\delta \omega_n)} \right )}=\frac{\omega _n^2}{s^2+2\delta \omega _ns+\omega _n^2}$$

's'の累乗は分母の項で2です。したがって、上記の伝達関数は2次であり、システムは次のようになります。second order system。

特性方程式は-

$$s^2+2\delta \omega _ns+\omega _n^2=0$$

特性方程式の根は-

$$s=\frac{-2\omega \delta _n\pm \sqrt{(2\delta\omega _n)^2-4\omega _n^2}}{2}=\frac{-2(\delta\omega _n\pm \omega _n\sqrt{\delta ^2-1})}{2}$$

$$\Rightarrow s=-\delta \omega_n \pm \omega _n\sqrt{\delta ^2-1}$$

• δ= 0の場合、2つの根は虚数です。
• δ= 1の場合、2つの根は実数で等しくなります。
• 2つの根は実数ですが、δ> 1の場合は等しくありません。
• 0 <δ<1の場合、2つの根は複素共役です。

私たちは書くことができます $C(s)$ 方程式として、

$$C(s)=\left ( \frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2} \right )R(s)$$

どこ、

• C(s) は出力信号のラプラス変換です。c（t）

• R(s) 入力信号のラプラス変換r（t）

• ω_n 固有振動数です

• δ は減衰比です。

次の手順に従って、時間領域で2次システムの応答（出力）を取得します。

• 入力信号のラプラス変換を行い、 $r(t)$。

• 方程式を考えてみましょう。 $C(s)=\left ( \frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2} \right )R(s)$

• 代替 $R(s)$ 上記の式の値。

• の部分分数を行う $C(s)$ もし必要なら。

• 逆ラプラス変換をに適用する $C(s)$。

二次システムのステップ応答

単位ステップ信号を2次システムへの入力と見なします。

単位ステップ信号のラプラス変換は、

$$R(s)=\frac{1}{s}$$

2次閉ループ制御システムの伝達関数は次のとおりです。

$$\frac{C(s)}{R(s)}=\frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$

ケース1：δ= 0

代替、 $\delta = 0$ 伝達関数で。

$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+\omega_n^2}$$

$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{s^2+\omega_n^2} \right )R(s)$$

代替、 $R(s) = \frac{1}{s}$ 上記の式で。

$$C(s)=\left( \frac{\omega_n^2}{s^2+\omega_n^2} \right )\left( \frac{1}{s} \right )=\frac{\omega_n^2}{s(s^2+\omega_n^2)}$$

両側に逆ラプラス変換を適用します。

$$c(t)=\left ( 1-\cos(\omega_n t) \right )u(t)$$

したがって、2次システムの単位ステップ応答は $/delta = 0$ 一定の振幅と周波数を持つ連続時間信号になります。

ケース2：δ= 1

代替、 $/delta = 1$ 伝達関数で。

$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+2\omega_ns+\omega_n^2}$$

$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{(s+\omega_n)^2} \right)R(s)$$

代替、 $R(s) = \frac{1}{s}$ 上記の式で。

$$C(s)=\left( \frac{\omega_n^2}{(s+\omega_n)^2} \right)\left ( \frac{1}{s} \right)=\frac{\omega_n^2}{s(s+\omega_n)^2}$$

の部分分数を行う $C(s)$。

$$C(s)=\frac{\omega_n^2}{s(s+\omega_n)^2}=\frac{A}{s}+\frac{B}{s+\omega_n}+\frac{C}{(s+\omega_n)^2}$$

単純化すると、A、B、Cの値が次のようになります。 $1,\: -1\: and \: −\omega _n$それぞれ。これらの値を上記の部分分数展開に代入します。$C(s)$。

$$C(s)=\frac{1}{s}-\frac{1}{s+\omega_n}-\frac{\omega_n}{(s+\omega_n)^2}$$

両側に逆ラプラス変換を適用します。

$$c(t)=(1-e^{-\omega_nt}-\omega _nte^{-\omega_nt})u(t)$$

したがって、2次システムの単位ステップ応答は、定常状態でステップ入力に到達しようとします。

ケース3：0 <δ<1

伝達関数の分母項を次のように変更できます-

$$s^2+2\delta\omega_ns+\omega_n^2=\left \{ s^2+2(s)(\delta \omega_n)+(\delta \omega_n)^2 \right \}+\omega_n^2-(\delta\omega_n)^2$$

$$=(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)$$

伝達関数は、

$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$

$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)} \right )R(s)$$

代替、 $R(s) = \frac{1}{s}$ 上記の式で。

$$C(s)=\left( \frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)} \right )\left( \frac{1}{s} \right )=\frac{\omega_n^2}{s\left ((s+\delta\omega_n)^2+\omega_n^2(1-\delta^2) \right)}$$

の部分分数を行う $C(s)$。

$$C(s)=\frac{\omega_n^2}{s\left ((s+\delta\omega_n)^2+\omega_n^2(1-\delta^2) \right)}=\frac{A}{s}+\frac{Bs+C}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$

単純化すると、A、B、Cの値が次のようになります。 $1,\: -1 \: and \: −2\delta \omega _n$それぞれ。これらの値を上記のC（s）の部分分数展開に代入します。

$$C(s)=\frac{1}{s}-\frac{s+2\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$

$$C(s)=\frac{1}{s}-\frac{s+\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}-\frac{\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$

$C(s)=\frac{1}{s}-\frac{(s+\delta\omega_n)}{(s+\delta\omega_n)^2+(\omega_n\sqrt{1-\delta^2})^2}-\frac{\delta}{\sqrt{1-\delta^2}}\left ( \frac{\omega_n\sqrt{1-\delta^2}}{(s+\delta\omega_n)^2+(\omega_n\sqrt{1-\delta^2})^2} \right )$

代替、 $\omega_n\sqrt{1-\delta^2}$ なので $\omega_d$ 上記の式で。

$$C(s)=\frac{1}{s}-\frac{(s+\delta\omega_n)}{(s+\delta\omega_n)^2+\omega_d^2}-\frac{\delta}{\sqrt{1-\delta^2}}\left ( \frac{\omega_d}{(s+\delta\omega_n)^2+\omega_d^2} \right )$$

両側に逆ラプラス変換を適用します。

$$c(t)=\left ( 1-e^{-\delta \omega_nt}\cos(\omega_dt)-\frac{\delta}{\sqrt{1-\delta^2}}e^{-\delta\omega_nt}\sin(\omega_dt) \right )u(t)$$

$$c(t)=\left ( 1-\frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}}\left ( (\sqrt{1-\delta^2})\cos(\omega_dt)+\delta \sin(\omega_dt) \right ) \right )u(t)$$

場合 $\sqrt{1-\delta^2}=\sin(\theta)$の場合、「δ」はcos（θ）になります。これらの値を上記の式に代入します。

$$c(t)=\left ( 1-\frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}}(\sin(\theta)\cos(\omega_dt)+\cos(\theta)\sin(\omega_dt)) \right )u(t)$$

$$\Rightarrow c(t)=\left ( 1-\left ( \frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta) \right )u(t)$$

したがって、2次システムの単位ステップ応答では、「δ」が0と1の間にあるときに、振動が減衰（振幅が減少）します。

ケース4：δ> 1

伝達関数の分母項を次のように変更できます-

$$s^2+2\delta\omega_ns+\omega_n^2=\left \{ s^2+2(s)(\delta\omega_n)+(\delta\omega_n)^2 \right \}+\omega_n^2-(\delta\omega_n)^2$$

$$=\left ( s+\delta\omega_n \right )^2-\omega_n^2\left ( \delta^2-1 \right )$$

伝達関数は、

$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{(s+\delta\omega_n)^2-\omega_n^2(\delta^2-1)}$$

$$\Rightarrow C(s)=\left ( \frac{\omega_n^2}{(s+\delta\omega_n)^2-\omega_n^2(\delta^2-1)} \right )R(s)$$

代替、 $R(s) = \frac{1}{s}$ 上記の式で。

$C(s)=\left ( \frac{\omega_n^2}{(s+\delta\omega_n)^2-(\omega_n\sqrt{\delta^2-1})^2} \right )\left ( \frac{1}{s} \right )=\frac{\omega_n^2}{s(s+\delta\omega_n+\omega_n\sqrt{\delta^2-1})(s+\delta\omega_n-\omega_n\sqrt{\delta^2-1})}$

の部分分数を行う $C(s)$。

$$C(s)=\frac{\omega_n^2}{s(s+\delta\omega_n+\omega_n\sqrt{\delta^2-1})(s+\delta\omega_n-\omega_n\sqrt{\delta^2-1})}$$

$$=\frac{A}{s}+\frac{B}{s+\delta\omega_n+\omega_n\sqrt{\delta^2-1}}+\frac{C}{s+\delta\omega_n-\omega_n\sqrt{\delta^2-1}}$$

単純化すると、A、B、Cの値が1になります。 $\frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}$ そして $\frac{-1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}$それぞれ。これらの値を上記の部分分数展開に代入します$C(s)$。

$$C(s)=\frac{1}{s}+\frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}\left ( \frac{1}{s+\delta\omega_n+\omega_n\sqrt{\delta^2-1}} \right )-\left ( \frac{1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )\left ( \frac{1}{s+\delta\omega_n-\omega_n\sqrt{\delta^2-1}} \right )$$

両側に逆ラプラス変換を適用します。

$c(t)=\left ( 1+\left ( \frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )e^{-(\delta\omega_n+\omega_n\sqrt{\delta^2-1})t}-\left ( \frac{1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )e^{-(\delta\omega_n-\omega_n\sqrt{\delta^2-1})t} \right )u(t)$

過減衰であるため、δ> 1の場合の2次システムの単位ステップ応答は、定常状態ではステップ入力に到達しません。

二次システムのインパルス応答

ザ・ impulse response 二次システムのは、これら2つの方法のいずれかを使用して取得できます。

• 次の値を考慮して、ステップ応答を導出する際の手順に従います。 $R(s)$ の代わりに1として $\frac{1}{s}$。

• ステップ応答の微分を行います。

次の表は、減衰比が4つの場合の2次システムのインパルス応答を示しています。

減衰比の条件	t≥0のインパルス応答
δ= 0	$\omega_n\sin(\omega_nt)$
δ= 1	$\omega_n^2te^{-\omega_nt}$
0 <δ<1	$\left ( \frac{\omega_ne^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt)$
δ> 1	$\left ( \frac{\omega_n}{2\sqrt{\delta^2-1}} \right )\left ( e^{-(\delta\omega_n-\omega_n\sqrt{\delta^2-1})t}-e^{-(\delta\omega_n+\omega_n\sqrt{\delta^2-1})t} \right )$

この章では、2次システムの時間領域仕様について説明します。次の図に、減衰不足の場合の2次システムのステップ応答を示します。

この図には、すべての時間領域の仕様が示されています。整定時間までの応答は過渡応答と呼ばれ、整定時間後の応答は定常状態応答と呼ばれます。

遅延時間

応答が到達するのに必要な時間です half of its final valueゼロの瞬間から。それはによって示されます$t_d$。

'δ'が0と1の間にある場合、t≥0の場合の2次システムのステップ応答を考慮してください。

$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$

ステップ応答の最終値は1です。

したがって、 $t=t_d$、ステップ応答の値は0.5になります。上記の式のこれらの値を代入します。

$$c(t_d)=0.5=1-\left ( \frac{e^{-\delta\omega_nt_d}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_d+\theta)$$

$$\Rightarrow \left ( \frac{e^{-\delta\omega_nt_d}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_d+\theta)=0.5$$

線形近似を使用すると、次のようになります。 delay time t_d なので

$$t_d=\frac{1+0.7\delta}{\omega_n}$$

立ち上がり時間

から応答が上がるのに必要な時間です 0% to 100% of its final value。これは、under-damped systems。過減衰システムの場合、最終値の10％から90％までの期間を考慮してください。立ち上がり時間はで表されますt_r。

t = t ₁ = 0で、c（t）= 0。

ステップ応答の最終値は1であることがわかっています。

したがって、 $t = t_2$、ステップ応答の値は1です。これらの値を次の式に代入します。

$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$

$$c(t_2)=1=1-\left ( \frac{e^{-\delta\omega_nt_2}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_2+\theta)$$

$$\Rightarrow \left ( \frac{e^{-\delta\omega_nt_2}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_2+\theta)=0$$

$$\Rightarrow \sin(\omega_dt_2+\theta)=0$$

$$\Rightarrow \omega_dt_2+\theta=\pi$$

$$\Rightarrow t_2=\frac{\pi-\theta}{\omega_d}$$

代替T ₁及びT _2つの次式の値rise time、

$$t_r=t_2-t_1$$

$$\therefore \: t_r=\frac{\pi-\theta}{\omega_d}$$

上記の式から、立ち上がり時間は次のように結論付けることができます。 $t_r$ と減衰周波数 $\omega_d$ 互いに反比例します。

ピーク時

応答がに到達するのに必要な時間です peak value初めて。それはによって示されます$t_p$。で$t = t_p$、応答の最初の導関数はゼロです。

減衰不足の場合の2次システムのステップ応答は次のようになります。

$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$

差別化する $c(t)$ 't'に関して。

$$\frac{\text{d}c(t)}{\text{d}t}=-\left ( \frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\omega_d\cos(\omega_dt+\theta)-\left ( \frac{-\delta\omega_ne^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$

代替、 $t=t_p$ そして $\frac{\text{d}c(t)}{\text{d}t}=0$ 上記の式で。

$$0=-\left ( \frac{e^{-\delta\omega_nt_p}}{\sqrt{1-\delta^2}} \right )\left [ \omega_d\cos(\omega_dt_p+\theta)-\delta\omega_n\sin(\omega_dt_p+\theta) \right ]$$

$$\Rightarrow \omega_n\sqrt{1-\delta^2}\cos(\omega_dt_p+\theta)-\delta\omega_n\sin(\omega_dt_p+\theta)=0$$

$$\Rightarrow \sqrt{1-\delta^2}\cos(\omega_dt_p+\theta)-\delta\sin(\omega_dt_p+\theta)=0$$

$$\Rightarrow \sin(\theta)\cos(\omega_dt_p+\theta)-\cos(\theta)\sin(\omega_dt_p+\theta)=0$$

$$\Rightarrow \sin(\theta-\omega_dt_p-\theta)=0$$

$$\Rightarrow sin(-\omega_dt_p)=0\Rightarrow -\sin(\omega_dt_p)=0\Rightarrow sin(\omega_dt_p)=0$$

$$\Rightarrow \omega_dt_p=\pi$$

$$\Rightarrow t_p=\frac{\pi}{\omega_d}$$

上記の式から、ピーク時間は次のように結論付けることができます。 $t_p$ と減衰周波数 $\omega_d$ 互いに反比例します。

ピークオーバーシュート

ピークオーバーシュート M_p応答の最終値からのピーク時の応答の偏差として定義されます。とも呼ばれますmaximum overshoot。

数学的には、次のように書くことができます

$$M_p=c(t_p)-c(\infty)$$

どこ、

c（t _p）は応答のピーク値です。

c（∞）は、応答の最終（定常状態）値です。

で $t = t_p$、応答c（t）は-

$$c(t_p)=1-\left ( \frac{e^{-\delta\omega_nt_p}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_p+\theta)$$

代替、 $t_p=\frac{\pi}{\omega_d}$ 上記の式の右辺にあります。

$$c(t_P)=1-\left ( \frac{e^{-\delta\omega_n\left ( \frac{\pi}{\omega_d} \right )}}{\sqrt{1-\delta^2}} \right )\sin\left ( \omega_d\left ( \frac{\pi}{\omega_d} \right ) +\theta\right )$$

$$\Rightarrow c(t_p)=1-\left ( \frac{e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}}{\sqrt{1-\delta^2}} \right )(-\sin(\theta))$$

私達はことを知っています

$$\sin(\theta)=\sqrt{1-\delta^2}$$

だから、私たちは得るでしょう $c(t_p)$ なので

$$c(t_p)=1+e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}$$

の値を代入します $c(t_p)$ そして $c(\infty)$ ピークオーバーシュート方程式で。

$$M_p=1+e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}-1$$

$$\Rightarrow M_p=e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}$$

Percentage of peak overshoot % $M_p$ この式を使用して計算できます。

$$\%M_p=\frac{M_p}{c(\infty )}\times 100\%$$

の値を代入することによって $M_p$ そして $c(\infty)$ 上記の式では、ピークオーバーシュートのパーセンテージを取得します $\%M_p$ なので

$$\%M_p=\left ( e^ {-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )} \right )\times 100\%$$

上記の式から、ピークオーバーシュートの割合は次のように結論付けることができます。 $\% M_p$ 減衰比が低下すると減少します $\delta$ 増加します。

整定時間

応答が定常状態に到達し、最終値の周りの指定された許容範囲内にとどまるのに必要な時間です。一般に、許容範囲は2％と5％です。整定時間はで表されます$t_s$。

5％の許容範囲の整定時間は-

$$t_s=\frac{3}{\delta\omega_n}=3\tau$$

2％の許容範囲の整定時間は-

$$t_s=\frac{4}{\delta\omega_n}=4\tau$$

どこ、 $\tau$ は時定数であり、 $\frac{1}{\delta\omega_n}$。

• 両方の整定時間 $t_s$ と時定数 $\tau$ 減衰比に反比例します $\delta$。

• 両方の整定時間 $t_s$ と時定数 $\tau$システムゲインとは無関係です。つまり、システムゲインの変化でさえ、整定時間です$t_s$ と時定数 $\tau$ 変わることはありません。

例

ここで、閉ループ伝達関数を持つ制御システムの時間領域仕様を見つけましょう。 $\frac{4}{s^2+2s+4}$ 単位ステップ信号がこの制御システムへの入力として適用されるとき。

2次閉ループ制御システムの伝達関数の標準形式は次のようになります。

$$\frac{\omega_n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$

これらの2つの伝達関数を等しくすることにより、減衰されていない固有振動数が得られます。 $\omega_n$ 2ラジアン/秒および減衰比として $\delta$ 0.5として。

減衰周波数の式を知っています $\omega_d$ なので

$$\omega_d=\omega_n\sqrt{1-\delta^2}$$

代替、 $\omega_n$ そして $\delta$ 上記の式の値。

$$\Rightarrow \omega_d=2\sqrt{1-(0.5)^2}$$

$$\Rightarrow \omega_d=1.732 \: rad/sec$$

代替、 $\delta$ 次の関係の値

$$\theta=\cos^{-1}\delta$$

$$\Rightarrow \theta=\cos^{-1}(0.5)=\frac{\pi}{3}\:rad$$

上記の必要な値を各時間領域仕様の式に代入し、単純化して、特定の伝達関数の時間領域仕様の値を取得します。

次の表に、時間領域の仕様、必要な値の置換、および最終値の式を示します。

時間領域の仕様	式	式の値の代入	最終値
遅延時間	$t_d=\frac{1+0.7\delta}{\omega_n}$	$t_d=\frac{1+0.7(0.5)}{2}$	$t_d$= 0.675秒
立ち上がり時間	$t_r=\frac{\pi-\theta}{\omega_d}$	$t_r=\frac{\pi-(\frac{\pi}{3})}{1.732}$	$t_r$= 1.207秒
ピーク時	$t_p=\frac{\pi}{\omega_d}$	$t_p=\frac{\pi}{1.732}$	$t_p$= 1.813秒
％ピークオーバーシュート	$\%M_p=\left( e^{-\left (\frac{\delta\pi}{\sqrt{1-\delta^2}} \right ) }\right )\times 100\%$	$\%M_p=\left( e^{-\left (\frac{0.5\pi}{\sqrt{1-(0.5)^2}} \right ) }\right )\times 100\%$	$\% \: M_p$= 16.32％
2％の許容範囲の整定時間	$t_s=\frac{4}{\delta\omega_n}$	$t_S=\frac{4}{(0.5)(2)}$	$t_s$= 4秒

定常状態での制御システムの出力の望ましい応答からの偏差は、次のように知られています。 steady state error。それはとして表されます$e_{ss}$。次のように、最終値の定理を使用して定常状態の誤差を見つけることができます。

$$e_{ss}=\lim_{t \to \infty}e(t)=\lim_{s \to 0}sE(s)$$

どこ、

E（s）は、エラー信号のラプラス変換です。 $e(t)$

ユニティフィードバックおよび非ユニティフィードバック制御システムの定常状態エラーを1つずつ見つける方法について説明します。

Unityフィードバックシステムの定常状態エラー

次の閉ループ制御システムのブロック図を検討してください。これは、単一の負のフィードバックを持っています。

どこ、

• R（s）は、基準入力信号のラプラス変換です。 $r(t)$
• C（s）は、出力信号のラプラス変換です。 $c(t)$

ユニティネガティブフィードバック閉ループ制御システムの伝達関数は次のようになります。

$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$

$$\Rightarrow C(s)=\frac{R(s)G(s)}{1+G(s)}$$

加算点の出力は-

$$E(s)=R(s)-C(s)$$

代替 $C(s)$ 上記の式の値。

$$E(s)=R(s)-\frac{R(s)G(s)}{1+G(s)}$$

$$\Rightarrow E(s)=\frac{R(s)+R(s)G(s)-R(s)G(s)}{1+G(s)}$$

$$\Rightarrow E(s)=\frac{R(s)}{1+G(s)}$$

代替 $E(s)$ 定常状態誤差式の値

$$e_{ss}=\lim_{s \to 0} \frac{sR(s)}{1+G(s)}$$

次の表は、単位ステップ、単位ランプ、単位放物線信号などの標準入力信号の定常状態誤差と誤差定数を示しています。

入力信号	定常状態エラー $e_{ss}$	エラー定数
ユニットステップ信号	$\frac{1}{1+k_p}$	$K_p=\lim_{s \to 0}G(s)$
ユニットランプ信号	$\frac{1}{K_v}$	$K_v=\lim_{s \to 0}sG(s)$
単位放物線信号	$\frac{1}{K_a}$	$K_a=\lim_{s \to 0}s^2G(s)$

どこ、 $K_p$、 $K_v$ そして $K_a$ それぞれ、位置誤差定数、速度誤差定数、加速度誤差定数です。

Note −上記の入力信号のいずれかが1以外の振幅を持っている場合は、対応する定常状態誤差にその振幅を掛けます。

Note−単位インパルス信号の定常状態誤差は、原点にのみ存在するため、定義できません。したがって、インパルス応答を単位インパルス入力と比較することはできません。t 無限大を示します。

例

入力信号の定常状態誤差を見つけましょう $r(t)=\left( 5+2t+\frac{t^2}{2} \right )u(t)$ ユニティネガティブフィードバック制御システムの $G(s)=\frac{5(s+4)}{s^2(s+1)(s+20)}$

与えられた入力信号は、ステップ、ランプ、放物線の3つの信号の組み合わせです。次の表に、これら3つの信号のエラー定数と定常状態エラー値を示します。

入力信号	エラー定数	定常状態エラー
$r_1(t)=5u(t)$	$K_p=\lim_{s \to 0}G(s)=\infty$	$e_{ss1}=\frac{5}{1+k_p}=0$
$r_2(t)=2tu(t)$	$K_v=\lim_{s \to 0}sG(s)=\infty$	$e_{ss2}=\frac{2}{K_v}=0$
$r_3(t)=\frac{t^2}{2}u(t)$	$K_a=\lim_{s \to 0}s^2G(s)=1$	$e_{ss3}=\frac{1}{k_a}=1$

上記の3つの定常状態エラーを追加することにより、全体的な定常状態エラーを取得します。

$$e_{ss}=e_{ss1}+e_{ss2}+e_{ss3}$$

$$\Rightarrow e_{ss}=0+0+1=1$$

したがって、定常状態エラーが発生しました $e_{ss}$ なので 1 この例では。

非ユニティフィードバックシステムの定常状態エラー

非ユニティ負帰還を持っている閉ループ制御システムの次のブロック図を考えてみましょう。

ユニティフィードバックシステムでのみ定常状態エラーを見つけることができます。したがって、非ユニティフィードバックシステムをユニティフィードバックシステムに変換する必要があります。このために、上記のブロック図に1つのユニティ正フィードバックパスと1つのユニティ負フィードバックパスを含めます。新しいブロック図は次のようになります。

ユニティネガティブフィードバックをそのままにして、上記のブロック図を簡略化します。以下は簡略化されたブロック図です。

このブロック図は、ユニティネガティブフィードバック閉ループ制御システムのブロック図に似ています。ここでは、単一のブロックが伝達関数を持っています$\frac{G(s)}{1+G(s)H(s)-G(s)}$ の代わりに $G(s)$。ユニティネガティブフィードバックシステムに与えられた定常状態誤差の式を使用して、定常状態誤差を計算できるようになりました。

Note−不安定な閉ループシステムの定常状態エラーを見つけることは無意味です。したがって、閉ループ安定システムについてのみ定常状態誤差を計算する必要があります。これは、定常状態のエラーを見つける前に、制御システムが安定しているかどうかを確認する必要があることを意味します。次の章では、概念に関連する安定性について説明します。

安定性は重要な概念です。この章では、システムの安定性と安定性に基づくシステムの種類について説明します。

安定性とは何ですか？

出力が制御されている場合、システムは安定していると言われます。そうでなければ、それは不安定であると言われます。Astable system 指定された有界入力に対して有界出力を生成します。

次の図は、安定したシステムの応答を示しています。

これは、単位ステップ入力に対する一次制御システムの応答です。この応答の値は0〜1です。したがって、出力は制限されます。単位ステップ信号は、のすべての正の値に対して1の値を持つことがわかっています。tゼロを含む。したがって、それは制限された入力です。したがって、入力と出力の両方が制限されているため、1次制御システムは安定しています。

安定性に基づくシステムの種類

安定性に基づいてシステムを次のように分類できます。

• 絶対に安定したシステム
• 条件付きで安定したシステム
• わずかに安定したシステム

絶対に安定したシステム

システムがシステムコンポーネント値のすべての範囲で安定している場合、それは absolutely stable system。開ループ伝達関数のすべての極が左半分に存在する場合、開ループ制御システムは完全に安定しています。‘s’ plane。同様に、閉ループ伝達関数のすべての極が「s」平面の左半分に存在する場合、閉ループ制御システムは完全に安定しています。

条件付きで安定したシステム

システムが特定の範囲のシステムコンポーネント値に対して安定している場合、それは次のように知られています。 conditionally stable system。

わずかに安定したシステム

制限された入力に対して一定の振幅と一定の振動周波数を持つ出力信号を生成することによってシステムが安定している場合、それは次のように知られています。 marginally stable system。開ループ伝達関数の任意の2つの極が虚軸上に存在する場合、開ループ制御システムはわずかに安定しています。同様に、閉ループ伝達関数の任意の2つの極が虚軸上に存在する場合、閉ループ制御システムはわずかに安定しています。

この章では、安定性解析について説明します。 ‘s’RouthHurwitz安定性基準を使用したドメイン。この基準では、閉ループ制御システムの安定性を見つけるための特性方程式が必要です。

ラウス・フルビッツ安定性基準

ラウス・フルビッツ安定性基準は、安定性のための1つの必要条件と1つの十分条件を持っています。いずれかの制御システムが必要条件を満たしていない場合、制御システムは不安定であると言えます。しかし、制御システムが必要条件を満たしている場合、それは安定している場合とそうでない場合があります。したがって、十分条件は、制御システムが安定しているかどうかを知るのに役立ちます。

ラウス・フルビッツ安定性の必要条件

必要条件は、特性多項式の係数が正でなければならないということです。これは、特性方程式のすべての根が負の実数部を持つ必要があることを意味します。

次数「n」の特性方程式が-であると考えてください。

$$a_0s^n+a_1s^{n-1}+a_2s^{n-2}+...+a_{n-1}s^1+a_ns^0=0$$

に欠落している用語があってはならないことに注意してください n^th次数特性方程式。これは、n^th 次数特性方程式には、ゼロ値の係数を含めないでください。

ラウス・フルビッツ安定性の十分条件

十分条件は、Routh配列の最初の列のすべての要素が同じ符号を持つ必要があることです。これは、Routh配列の最初の列のすべての要素が正または負のいずれかである必要があることを意味します。

ラウスアレイ法

特性方程式のすべての根が「s」平面の左半分に存在する場合、制御システムは安定しています。特性方程式の少なくとも1つの根が「s」平面の右半分に存在する場合、制御システムは不安定です。したがって、制御システムが安定しているか不安定であるかを知るには、特性方程式の根を見つける必要があります。しかし、次数が増えるにつれて、特性方程式の根を見つけることは困難です。

したがって、この問題を克服するために、 Routh array method。この方法では、特性方程式の根を計算する必要はありません。最初にRouthテーブルを作成し、Routhテーブルの最初の列で符号の変更の数を見つけます。Routhテーブルの最初の列の符号の変化の数は、「s」平面の右半分に存在する特性方程式の根の数を示し、制御システムは不安定です。

この手順に従って、Routhテーブルを作成します。

• 以下の表に記載されているように、Routh配列の最初の2行に特性多項式の係数を入力します。の係数から始めます$s^n$ の係数まで続けます $s^0$。

• 以下の表に記載されているように、Routh配列の残りの行に要素を入力します。の最初の列要素を取得するまで、このプロセスを続けますrow $s^0$ です $a_n$。ここに、$a_n$ の係数は $s^0$ 特性多項式で。

Note − Routhテーブルの行要素に共通の要素がある場合は、その要素で行要素を分割して簡単にすることができます。

次の表は、n^次の標数多項式のラウス配列を示しています。

$$a_0s^n+a_1s^{n-1}+a_2s^{n-2}+...+a_{n-1}s^1+a_ns^0$$

$s^n$	$a_0$	$a_2$	$a_4$	$a_6$	..。	..。
$s^{n-1}$	$a_1$	$a_3$	$a_5$	$a_7$	..。	..。
$s^{n-2}$	$b_1=\frac{a_1a_2-a_3a_0}{a_1}$	$b_2=\frac{a_1a_4-a_5a_0}{a_1}$	$b_3=\frac{a_1a_6-a_7a_0}{a_1}$	..。	..。	..。
$s^{n-3}$	$c_1=\frac{b_1a_3-b_2a_1}{b_1}$	$c_2=\frac{b_1a_55-b_3a_1}{b_1}$	$\vdots$
$\vdots $	$\vdots$	$\vdots$	$\vdots$
$s^1$	$\vdots$	$\vdots$
$s^0$	$a_n$

Example

特性方程式を持つ制御システムの安定性を見つけましょう。

$$s^4+3s^3+3s^2+2s+1=0$$

Step 1 −Routh-Hurwitzの安定性に必要な条件を確認します。

特性多項式のすべての係数、 $s^4+3s^3+3s^2+2s+1$ポジティブです。したがって、制御システムは必要条件を満たします。

Step 2 −与えられた特性多項式のラウス配列を形成します。

$s^4$	$1$	$3$	$1$
$s^3$	$3$	$2$
$s^2$	$\frac{(3 \times 3)-(2 \times 1)}{3}=\frac{7}{3}$	$\frac{(3 \times 1)-(0 \times 1)}{3}=\frac{3}{3}=1$
$s^1$	$\frac{\left ( \frac{7}{3}\times 2 \right )-(1 \times 3)}{\frac{7}{3}}=\frac{5}{7}$
$s^0$	$1$

Step 3 −Routh-Hurwitzの安定性のための十分条件を確認します。

Routh配列の最初の列のすべての要素は正です。Routh配列の最初の列に符号の変更はありません。したがって、制御システムは安定しています。

ラウスアレイの特殊なケース

Routhテーブルを作成しているときに、2つのタイプの状況に遭遇する可能性があります。これらの2つの状況からRouthテーブルを完成させることは困難です。

2つの特殊なケースは次のとおりです。

• Routh配列の任意の行の最初の要素はゼロです。
• Routh配列の任意の行のすべての要素はゼロです。

ここで、これら2つのケースの問題を1つずつ克服する方法について説明します。

Routh配列の任意の行の最初の要素がゼロです

Routh配列のいずれかの行にゼロとして最初の要素のみが含まれ、残りの要素の少なくとも1つがゼロ以外の値である場合、最初の要素を小さな正の整数に置き換えます。 $\epsilon$。次に、Routhテーブルを完成させるプロセスを続行します。ここで、次のように代入して、Routhテーブルの最初の列で符号の変更の数を見つけます。$\epsilon$ ゼロになる傾向があります。

Example

特性方程式を持つ制御システムの安定性を見つけましょう。

$$s^4+2s^3+s^2+2s+1=0$$

Step 1 −Routh-Hurwitzの安定性に必要な条件を確認します。

特性多項式のすべての係数、 $s^4+2s^3+s^2+2s+1$ポジティブです。そのため、制御システムは必要条件を満たしていました。

Step 2 −与えられた特性多項式のラウス配列を形成します。

$s^4$	$1$	$1$	$1$
$s^3$	2 1	2 1
$s^2$	$\frac{(1 \times 1)-(1 \times 1)}{1}=0$	$\frac{(1 \times 1)-(0 \times 1)}{1}=1$
$s^1$
$s^0$

行 $s^3$要素には、共通因子として2があります。したがって、これらの要素はすべて2で除算されます。

Special case (i) −行の最初の要素のみ $s^2$はゼロです。だから、それをに置き換えます$\epsilon$ そして、Routhテーブルを完成させるプロセスを続行します。

$s^4$	1	1	1
$s^3$	1	1
$s^2$	$\epsilon$	1
$s^1$	$\frac{\left ( \epsilon \times 1 \right )-\left ( 1 \times 1 \right )}{\epsilon}=\frac{\epsilon-1}{\epsilon}$
$s^0$	1

Step 3 −Routh-Hurwitzの安定性のための十分条件を確認します。

なので $\epsilon$ ゼロになる傾向があるため、Routhテーブルは次のようになります。

$s^4$	1	1	1
$s^3$	1	1
$s^2$	0	1
$s^1$	-∞
$s^0$	1

Routhテーブルの最初の列に2つの符号の変更があります。したがって、制御システムは不安定です。

Routh配列の任意の行のすべての要素がゼロです

この場合、次の2つの手順に従います-

• ゼロの行のすぐ上にある行の補助方程式A（s）を記述します。

• 補助方程式A（s）をsに関して微分します。ゼロの行をこれらの係数で埋めます。

Example

特性方程式を持つ制御システムの安定性を見つけましょう。

$$s^5+3s^4+s^3+3s^2+s+3=0$$

Step 1 −Routh-Hurwitzの安定性に必要な条件を確認します。

与えられた特性多項式のすべての係数は正です。そのため、制御システムは必要条件を満たしていました。

Step 2 −与えられた特性多項式のラウス配列を形成します。

$s^5$	1	1	1
$s^4$	3 1	3 1	3 1
$s^3$	$\frac{(1 \times 1)-(1 \times 1)}{1}=0$	$\frac{(1 \times 1)-(1 \times 1)}{1}=0$
$s^2$
$s^1$
$s^0$

行 $s^4$ 要素の公約数は3です。したがって、これらの要素はすべて3で除算されます。

Special case (ii) −行のすべての要素 $s^3$ゼロです。したがって、行の補助方程式A（s）を記述します。$s^4$。

$$A(s)=s^4+s^2+1$$

上記の式をsに関して微分します。

$$\frac{\text{d}A(s)}{\text{d}s}=4s^3+2s$$

これらの係数を行に配置します $s^3$。

$s^5$	1	1	1
$s^4$	1	1	1
$s^3$	4 2	2 1
$s^2$	$\frac{(2 \times 1)-(1 \times 1)}{2}=0.5$	$\frac{(2 \times 1)-(0 \times 1)}{2}=1$
$s^1$	$\frac{(0.5 \times 1)-(1 \times 2)}{0.5}=\frac{-1.5}{0.5}=-3$
$s^0$	1

Step 3 −Routh-Hurwitzの安定性のための十分条件を確認します。

Routhテーブルの最初の列に2つの符号の変更があります。したがって、制御システムは不安定です。

ラウス・フルビッツ安定性基準では、閉ループ極が「s」平面の左半分にあるか、「s」平面の右半分にあるか、または虚軸上にあるかを知ることができます。そのため、制御システムの性質を見つけることができません。この制限を克服するために、根軌跡として知られる手法があります。この手法については、次の2つの章で説明します。

根軌跡図では、閉ループ極の経路を観察できます。したがって、制御システムの性質を特定できます。この手法では、開ループ伝達関数を使用して、閉ループ制御システムの安定性を確認します。

根軌跡の基礎

根軌跡は、システムゲインKをゼロから無限大まで変化させることによる特性方程式の根の軌跡です。

閉ループ制御システムの特性方程式は次のとおりです。

$$1+G(s)H(s)=0$$

私たちは表現することができます $G(s)H(s)$ なので

$$G(s)H(s)=K\frac{N(s)}{D(s)}$$

どこ、

• Kは倍率を表します

• N（s）は、「s」の（因数分解された）n^次多項式を持つ分子項を表します。

• D（s）は、「s」の（因数分解された）m^次多項式を持つ分母項を表します。

代替、 $G(s)H(s)$ 特性方程式の値。

$$1+k\frac{N(s)}{D(s)}=0$$

$$\Rightarrow D(s)+KN(s)=0$$

Case 1 − K = 0

場合 $K=0$、その後 $D(s)=0$。

つまり、Kがゼロの場合、閉ループ極は開ループ極と等しくなります。

Case 2 − K = ∞

上記の特性方程式を次のように書き直します。

$$K\left(\frac{1}{K}+\frac{N(s)}{D(s)} \right )=0 \Rightarrow \frac{1}{K}+\frac{N(s)}{D(s)}=0$$

代替、 $K = \infty$ 上記の式で。

$$\frac{1}{\infty}+\frac{N(s)}{D(s)}=0 \Rightarrow \frac{N(s)}{D(s)}=0 \Rightarrow N(s)=0$$

場合 $K=\infty$、その後 $N(s)=0$。これは、Kが無限大の場合、閉ループの極が開ループの零点に等しいことを意味します。

上記の2つのケースから、根軌跡の分岐は開ループの極で始まり、開ループの零点で終わると結論付けることができます。

角度条件と大きさ条件

根軌跡分岐上の点は角度条件を満たす。したがって、角度条件は、点が根軌跡の分岐に存在するかどうかを知るために使用されます。マグニチュード条件を使用して、根軌跡分岐上の点のKの値を見つけることができます。したがって、点の大きさの条件を使用でき、これは角度の条件を満たします。

閉ループ制御システムの特性方程式は次のとおりです。

$$1+G(s)H(s)=0$$

$$\Rightarrow G(s)H(s)=-1+j0$$

ザ・ phase angle の $G(s)H(s)$ です

$$\angle G(s)H(s)=\tan^{-1}\left ( \frac{0}{-1} \right )=(2n+1)\pi$$

ザ・ angle condition開ループ伝達関数の角度が1800の奇数倍になる^点です。

の大きさ $G(s)H(s)$ は-

$$|G(s)H(s)|=\sqrt {(-1)^2+0^2}=1$$

大きさの条件は、開ループ伝達関数の大きさが1になる点（角度条件を満たす）です。

ザ・ root locusはsドメインのグラフィック表現であり、実際の軸に対して対称です。開ループの極と零点は、実数または複素共役のペアとして値を持つsドメインに存在するためです。この章では、根軌跡を作成（描画）する方法について説明します。

根軌跡の構築規則

根軌跡を作成するには、次のルールに従ってください。

Rule 1 −「s」平面で開ループの極と零点を見つけます。

Rule 2 −根軌跡の枝の数を見つけます。

根軌跡の分岐は、開ループの極で始まり、開ループの零点で終わることがわかっています。だから、根軌跡の枝の数N 有限開ループ極の数に等しい P または有限開ループ零点の数 Z、どちらか大きい方。

数学的には、根軌跡の枝の数を書くことができます N なので

$N=P$ もし $P\geq Z$

$N=Z$ もし $P<Z$

Rule 3 −識別して描画する real axis root locus branches。

点での開ループ伝達関数の角度は、180の奇数倍である場合は⁰、その点は、根軌跡上にあります。実軸上の点の左側に奇数の開ループ極と零点が存在する場合、その点は根軌跡分岐上にあります。したがって、この条件を満たす点の分岐は、根軌跡分岐の実軸です。

Rule 4 −重心と漸近線の角度を見つけます。

• 場合 $P = Z$、次に、すべての根軌跡分岐は、有限の開ループ極で始まり、有限の開ループ零点で終わります。

• 場合 $P > Z$ 、その後 $Z$ 根軌跡分岐の数は、有限の開ループ極で始まり、有限の開ループ零点で終わります。 $P − Z$ 根軌跡分岐の数は、有限の開ループ極で始まり、無限の開ループ零点で終わります。

• 場合 $P < Z$ 、次に、P個の根軌跡分岐が有限開ループ極で始まり、有限開ループ零点で終わり、 $Z − P$ 根軌跡分岐の数は、無限の開ループ極で始まり、有限の開ループ零点で終わります。

したがって、根軌跡の分岐の一部は、次の場合に無限大に近づきます。 $P \neq Z$。漸近線は、これらの根軌跡の分岐の方向を示します。実軸上の漸近線の交点は、centroid。

私たちは計算することができます centroid α この式を使用することにより、

$\alpha = \frac{\sum Real\: part\: of\: finite\: open\: loop\: poles\:-\sum Real\: part\: of\: finite\: open\: loop\: zeros}{P-Z}$

の角度の式 asymptotes θ です

$$\theta=\frac{(2q+1)180^0}{P-Z}$$

どこ、

$$q=0,1,2,....,(P-Z)-1$$

Rule 5 −仮想軸を持つ根軌跡分岐の交点を見つけます。

根軌跡の枝が虚軸と交差する点との値を計算できます。 K その時点で、ラウス配列法と特別な方法を使用して case (ii)。

• Routh配列の任意の行のすべての要素がゼロの場合、根軌跡の分岐は虚軸と交差し、その逆も同様です。

• 最初の要素をゼロにすると、行全体の要素がゼロになるように行を識別します。の値を見つけるK この組み合わせのために。

• これに置き換えてください K補助方程式の値。根軌跡枝と仮想軸の交点を取得します。

Rule 6 −ブレークアウェイポイントとブレークインポイントを見つけます。

• 2つの開ループ極の間に実軸根軌跡分岐が存在する場合、 break-away point これらの2つの開ループ極の間。

• 2つの開ループゼロの間に実軸根軌跡分岐が存在する場合、 break-in point これらの2つの開ループゼロの間。

Note −ブレークアウェイポイントとブレークインポイントは、実軸の根軌跡の分岐にのみ存在します。

次の手順に従って、ブレークアウェイポイントとブレークインポイントを見つけます。

• 書く $K$ の面では $s$ 特性方程式から $1 + G(s)H(s) = 0$。

• 差別化する $K$sに関して、ゼロに等しくします。これらの値を$s$ 上記の式で。

• の値 $s$ そのために $K$ 値が正の場合 break points。

Rule 7 −出発角度と到着角度を見つけます。

出発角度と到着角度は、それぞれ複素共役開ループ極と複素共役開ループ零点で計算できます。

の式 angle of departure $\phi_d$ です

$$\phi_d=180^0-\phi$$

の式 angle of arrival $\phi_a$ です

$$\phi_a=180^0+\phi$$

どこ、

$$\phi=\sum \phi_P-\sum \phi_Z$$

例

ここで、開ループ伝達関数を持つ制御システムの根軌跡を描きましょう。 $G(s)H(s)=\frac{K}{s(s+1)(s+5)}$

Step 1 −与えられた開ループ伝達関数には、次の3つの極があります。 $s = 0, s = −1$ そして $s = −5$。ゼロはありません。したがって、根軌跡の分岐の数は、開ループ伝達関数の極の数と同じです。

$$N=P=3$$

上図に示すように、3つの極が配置されています。間の線分$s = −1$ そして $s = 0$実軸上の根軌跡の1つの分岐です。そして、実軸上の根軌跡の他の分岐は、の左側の線分です。$s = −5$。

Step 2 −与えられた式を使用して、重心の値と漸近線の角度を取得します。

セントロイド $\alpha = −2$

漸近線の角度は $\theta = 60^0,180^0$ そして $300^0$。

次の図に、重心と3つの漸近線を示します。

Step 3 −2つの漸近線の角度は $60^0$ そして $300^0$、2つの根軌跡分岐が虚軸と交差します。ラウス配列法と特殊なケース（ii）を使用することにより、根軌跡の分岐はで虚軸と交差します。$j\sqrt{5}$ そして $−j\sqrt{5}$。

極間の実軸根軌跡分岐上に1つのブレークアウェイポイントがあります $s = −1$ そして $s = 0$。ブレークアウェイポイントの計算に与えられた手順に従うことにより、次のようになります。$s = −0.473$。

与えられた制御システムの根軌跡図を次の図に示します。

このようにして、任意の制御システムの根軌跡図を描画し、閉ループ伝達関数の極の動きを観察できます。

根軌跡図から、さまざまなタイプの減衰のK値の範囲を知ることができます。

根軌跡に対する開ループ極と零点の追加の影響

根軌跡はシフトインできます ‘s’ plane 開ループ極と開ループ零点を追加します。

• 開ループ伝達関数に極を含めると、根軌跡の分岐の一部が「s」平面の右半分に向かって移動します。このため、減衰比$\delta$減少します。つまり、減衰周波数$\omega_d$ 増加し、遅延時間などの時間領域仕様 $t_d$、 立ち上がり時間 $t_r$ とピーク時間 $t_p$減少。ただし、システムの安定性に影響します。

• 開ループ伝達関数にゼロを含めると、根軌跡分岐の一部が「s」平面の左半分に向かって移動します。したがって、制御システムの安定性が向上します。この場合、減衰比$\delta$増加します。つまり、減衰周波数$\omega_d$ 減少し、遅延時間などの時間領域仕様 $t_d$、 立ち上がり時間 $t_r$ とピーク時間 $t_p$ 増加する。

したがって、要件に基づいて、伝達関数に開ループの極または零点を含める（追加する）ことができます。

制御システムの時間応答解析と2次制御システムの時間領域仕様についてはすでに説明しました。この章では、制御システムの周波数応答解析と2次制御システムの周波数領域仕様について説明します。

周波数応答とは何ですか？

システムの応答は、過渡応答と定常状態応答の両方に分割できます。フーリエ積分を使用して過渡応答を見つけることができます。入力正弦波信号に対するシステムの定常状態応答は、frequency response。この章では、定常状態の応答のみに焦点を当てます。

正弦波信号が線形時不変（LTI）システムへの入力として適用されると、定常状態の出力が生成されます。これも正弦波信号です。入力と出力の正弦波信号の周波数は同じですが、振幅と位相角が異なります。

入力信号を−とする

$$r(t)=A\sin(\omega_0t)$$

開ループ伝達関数は次のようになります-

$$G(s)=G(j\omega)$$

私たちは表現することができます $G(j\omega)$ 以下に示すように、大きさと位相の観点から。

$$G(j\omega)=|G(j\omega)| \angle G(j\omega)$$

代替、 $\omega = \omega_0$ 上記の式で。

$$G(j\omega_0)=|G(j\omega_0)| \angle G(j\omega_0)$$

出力信号は

$$c(t)=A|G(j\omega_0)|\sin(\omega_0t + \angle G(j\omega_0))$$

• ザ・ amplitude 出力正弦波信号の振幅は、入力正弦波信号の振幅との大きさを乗算することによって得られます。 $G(j\omega)$ で $\omega = \omega_0$。

• ザ・ phase 出力正弦波信号の位相は、入力正弦波信号の位相との位相を加算することによって得られます。 $G(j\omega)$ で $\omega = \omega_0$。

どこ、

• A 入力正弦波信号の振幅です。

• ω₀ 入力正弦波信号の角周波数です。

書くことができる、角周波数 $\omega_0$ 以下に示すように。

$$\omega_0=2\pi f_0$$

ここに、 $f_0$入力正弦波信号の周波数です。同様に、閉ループ制御システムについても同じ手順に従うことができます。

周波数領域の仕様

周波数領域の仕様は次のとおりです。 resonant peak, resonant frequency and bandwidth。

2次閉ループ制御システムの伝達関数を次のように考えます。

$$T(s)=\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$

代替、 $s = j\omega$ 上記の式で。

$$T(j\omega)=\frac{\omega_n^2}{(j\omega)^2+2\delta\omega_n(j\omega)+\omega_n^2}$$

$$\Rightarrow T(j\omega)=\frac{\omega_n^2}{-\omega^2+2j\delta\omega\omega_n+\omega_n^2}=\frac{\omega_n^2}{\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )}$$

$$\Rightarrow T(j\omega)=\frac{1}{\left ( 1-\frac{\omega^2}{\omega_n^2} \right )+j\left ( \frac{2\delta\omega}{\omega_n} \right )}$$

しましょう、 $\frac{\omega}{\omega_n}=u$ この値を上記の式に代入します。

$$T(j\omega)=\frac{1}{(1-u^2)+j(2\delta u)}$$

の大きさ $T(j\omega)$ は-

$$M=|T(j\omega)|=\frac{1}{\sqrt {(1-u^2)^2+(2\delta u)^2}}$$

のフェーズ $T(j\omega)$ は-

$$\angle T(j\omega)=-tan^{-1}\left( \frac{2\delta u}{1-u^2} \right )$$

共鳴周波数

周波数応答の大きさが初めてピーク値になる周波数です。それはによって示されます$\omega_r$。で$\omega = \omega_r$、の大きさの最初の導関数 $T(j\omega)$ はゼロです。

差別化する $M$ に関して $u$。

$$\frac{\text{d}M}{\text{d}u}=-\frac{1}{2}\left [ (1-u^2)^2+(2\delta u)^2 \right ]^{\frac{-3}{2}} \left [2(1-u^2)(-2u)+2(2\delta u)(2\delta) \right ]$$

$$\Rightarrow \frac{\text{d}M}{\text{d}u}=-\frac{1}{2}\left [ (1-u^2)^2+(2\delta u)^2 \right ]^{\frac{-3}{2}} \left [4u(u^2-1 +2\delta^2) \right ]$$

代替、 $u=u_r$ そして $\frac{\text{d}M}{\text{d}u}==0$ 上記の式で。

$$0=-\frac{1}{2}\left [ (1-u_r^2)^2+(2\delta u_r)^2 \right ]^{-\frac{3}{2}}\left [ 4u_r(u_r^2-1 +2\delta^2) \right ]$$

$$\Rightarrow 4u_r(u_r^2-1 +2\delta^2)=0$$

$$\Rightarrow u_r^2-1+2\delta^2=0$$

$$\Rightarrow u_r^2=1-2\delta^2$$

$$\Rightarrow u_r=\sqrt{1-2\delta^2}$$

代替、 $u_r=\frac{\omega_r}{\omega_n}$ 上記の式で。

$$\frac{\omega_r}{\omega_n}=\sqrt{1-2\delta^2}$$

$$\Rightarrow \omega_r=\omega_n \sqrt{1-2\delta^2}$$

レゾナントピーク

の大きさのピーク（最大）値です $T(j\omega)$。それはによって示されます$M_r$。

で $u = u_r$、の大きさ $T(j\omega)$ は-

$$M_r=\frac{1}{\sqrt{(1-u_r^2)^2+(2\delta u_r)^2}}$$

代替、 $u_r = \sqrt{1 − 2\delta^2}$ そして $1 − u_r^2 = 2\delta^2$ 上記の式で。

$$M_r=\frac{1}{\sqrt{(2\delta^2)^2+(2\delta \sqrt{1-2\delta^2})^2}}$$

$$\Rightarrow M_r=\frac{1}{2\delta \sqrt {1-\delta^2}}$$

周波数応答の共振ピークは、減衰比の特定の値に対する時間領域の過渡応答のピークオーバーシュートに対応します $\delta$。したがって、共振ピークとピークオーバーシュートは互いに相関しています。

帯域幅

それは周波数の範囲であり、その大きさは $T(j\omega)$ ゼロ周波数値から70.7％に低下します。

で $\omega = 0$、の値 $u$ ゼロになります。

代替、 $u = 0$ Mで。

$$M=\frac{1}{\sqrt {(1-0^2)^2+(2\delta(0))^2}}=1$$

したがって、 $T(j\omega)$ で1つです $\omega = 0$。

3 dBの周波数では、 $T(j\omega)$ の大きさの70.7％になります $T(j\omega)$ で $\omega = 0$。

私は食べる $\omega = \omega_B, M = 0.707(1) = \frac{1}{\sqrt{2}}$

$$\Rightarrow M=\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{(1-u_b^2)^2+(2\delta u_b)^2}}$$

$$\Rightarrow 2=(1-u_b^2)^2+(2\delta)^2 u_b^2$$

しましょう、 $u_b^2=x$

$$\Rightarrow 2=(1-x)^2+(2\delta)^2 x$$

$$\Rightarrow x^2+(4\delta^2-2)x-1=0$$

$$\Rightarrow x=\frac{-(4\delta^2 -2)\pm \sqrt{(4\delta^2-2)^2+4}}{2}$$

xの正の値のみを考慮してください。

$$x=1-2\delta^2+\sqrt {(2\delta^2-1)^2+1}$$

$$\Rightarrow x=1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}$$

代替、 $x=u_b^2=\frac{\omega_b^2}{\omega_n^2}$

$$\frac{\omega_b^2}{\omega_n^2}=1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}$$

$$\Rightarrow \omega_b=\omega_n \sqrt {1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}}$$

帯域幅 $\omega_b$ 周波数応答の変化は立ち上がり時間に反比例します $t_r$ 時間領域の過渡応答で。

ボード線図またはボード線図は、2つのプロットで構成されます-

• マグニチュードプロット
• 位相プロット

両方のプロットで、x軸は角周波数（対数目盛）を表します。一方、yaxisは、振幅プロットの開ループ伝達関数の大きさ（線形スケール）と、位相プロットの開ループ伝達関数の位相角（線形スケール）を表します。

ザ・ magnitude dB単位の開ループ伝達関数のは-

$$M=20\: \log|G(j\omega)H(j\omega)|$$

ザ・ phase angle 開ループ伝達関数の度数は-

$$\phi=\angle G(j\omega)H(j\omega)$$

Note −対数の底は10です。

ボード線図の基本

次の表は、開ループ伝達関数に存在する項の傾き、大きさ、および位相角の値を示しています。このデータは、ボード線図を描くときに役立ちます。

用語の種類	G（jω）H（jω）	スロープ（dB / dec）	マグニチュード（dB）	位相角（度）
絶え間ない	$K$	$0$	$20 \log K$	$0$
原点ゼロ	$j\omega$	$20$	$20 \log \omega$	$90$
原点の「n」ゼロ	$(j\omega)^n$	$20\: n$	$20\: n \log \omega$	$90\: n$
原点のポール	$\frac{1}{j\omega}$	$-20$	$-20 \log \omega$	$-90 \: or \: 270$
原点の「n」極	$\frac{1}{(j\omega)^n}$	$-20\: n$	$-20 \: n \log \omega$	$-90 \: n \: or \: 270 \: n$
単純なゼロ	$1+j\omega r$	$20$	$0\: for\: \omega < \frac{1}{r}$ $20\: \log \omega r\: for \: \omega > \frac{1}{r}$	$0 \: for \: \omega < \frac{1}{r}$ $90 \: for \: \omega > \frac{1}{r}$
シンプルポール	$\frac{1}{1+j\omega r}$	$-20$	$0\: for\: \omega < \frac{1}{r}$ $-20\: \log \omega r\: for\: \omega > \frac{1}{r}$	$0 \: for \: \omega < \frac{1}{r}$ $-90\: or \: 270 \: for\: \omega > \frac{1}{r}$
二次微分項	$\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )$	$40$	$40\: \log\: \omega_n\: for \: \omega < \omega_n$ $20\: \log\:(2\delta\omega_n^2)\: for \: \omega=\omega_n$ $40 \: \log \: \omega\:for \:\omega > \omega_n$	$0 \: for \: \omega < \omega_n$ $90 \: for \: \omega = \omega_n$ $180 \: for \: \omega > \omega_n$
二次積分項	$\frac{1}{\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )}$	$-40$	$-40\: \log\: \omega_n\: for \: \omega < \omega_n$ $-20\: \log\:(2\delta\omega_n^2)\: for \: \omega=\omega_n$ $-40 \: \log \: \omega\:for \:\omega > \omega_n$	$-0 \: for \: \omega < \omega_n$ $-90 \: for \: \omega = \omega_n$ $-180 \: for \: \omega > \omega_n$

開ループ伝達関数を検討してください $G(s)H(s) = K$。

マグニチュード $M = 20\: \log K$ dB

位相角 $\phi = 0$ 度

場合 $K = 1$の場合、大きさは0dBです。

場合 $K > 1$、その場合、大きさは正になります。

場合 $K < 1$の場合、大きさは負になります。

次の図は、対応するボード線図を示しています。

振幅プロットは、周波数に依存しない水平線です。Kの値が1の場合、0dBの線自体が振幅プロットです。Kの正の値の場合、水平線はシフトします$20 \:\log K$0dBラインより上のdB。Kの負の値の場合、水平線はシフトします$20\: \log K$0dBラインよりdB低い。ゼロ度の線自体は、Kのすべての正の値の位相プロットです。

開ループ伝達関数を検討してください $G(s)H(s) = s$。

マグニチュード $M = 20 \log \omega$ dB

位相角 $\phi = 90^0$

で $\omega = 0.1$ ラジアン/秒、大きさは-20dBです。

で $\omega = 1$ ラジアン/秒、大きさは0dBです。

で $\omega = 10$ ラジアン/秒、大きさは20dBです。

次の図は、対応するボード線図を示しています。

振幅プロットは線であり、20 dB / decの傾きを持っています。この行はで始まりました$\omega = 0.1$-20 dBの大きさのラジアン/秒で、同じ勾配で継続します。で0dBラインに触れています$\omega = 1$ラジアン/秒 この場合、位相プロットは、90である⁰行。

開ループ伝達関数を検討してください $G(s)H(s) = 1 + s\tau$。

マグニチュード $M = 20\: log \sqrt{1 + \omega^2\tau^2}$ dB

位相角 $\phi = \tan^{-1}\omega\tau$ 度

にとって $ω < \frac{1}{\tau}$ 、大きさは0 dB、位相角は0度です。

にとって $\omega > \frac{1}{\tau}$ 、大きさは $20\: \log \omega\tau$デシベルと位相角は90である⁰。

次の図は、対応するボード線図を示しています。

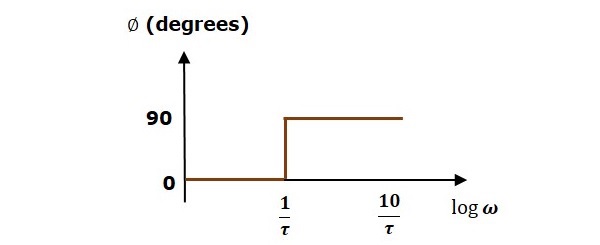
振幅プロットは、最大0dBの振幅を持っています $\omega=\frac{1}{\tau}$ラジアン/秒 から$\omega = \frac{1}{\tau}$ラジアン/秒、20 dB / decの傾きがあります。この場合、位相プロットの位相角は0度から$\omega = \frac{1}{\tau}$ラジアン/秒で、ここから、位相角は900になり^ます。このボード線図は、asymptotic Bode plot。

振幅と位相のプロットは直線で表されるため、正確なボード線図は漸近的なボード線図に似ています。唯一の違いは、正確なボード線図が直線ではなく単純な曲線を持つことです。

同様に、表に示されている開ループ伝達関数の他の項のボード線図を描くことができます。

この章では、ボード線図を作成（描画）する方法を詳しく理解しましょう。

ボード線図の構築に関する規則

ボード線図を作成するときは、これらのルールに従ってください。

• 開ループ伝達関数を標準の時定数形式で表します。

• 代替、 $s=j\omega$ 上記の式で。

• コーナー周波数を見つけて、昇順で並べます。

• 1/10としてボード線図の開始周波数を考慮^番目に小さい値である方最小コーナー周波数の又は0.1ラジアン/秒と10倍、最大コーナー周波数点で最大ボード線図を描きます。

• 各項のマグニチュードプロットを描画し、これらのプロットを適切に組み合わせます。

• 各項の位相プロットを描き、これらのプロットを適切に組み合わせます。

Note −コーナー周波数は、マグニチュードプロットの傾きが変化する周波数です。

例

閉ループ制御システムの開ループ伝達関数を検討してください

$$G(s)H(s)=\frac{10s}{(s+2)(s+5)}$$

この開ループ伝達関数を標準の時定数形式に変換してみましょう。

$$G(s)H(s)=\frac{10s}{2\left( \frac{s}{2}+1 \right )5 \left( \frac{s}{5}+1 \right )}$$

$$\Rightarrow G(s)H(s)=\frac{s}{\left( 1+\frac{s}{2} \right )\left( 1+\frac{s}{5} \right )}$$

したがって、前述のルールを使用して、片対数シートにボード線図を描くことができます。

ボード線図を使用した安定性分析

ボード線図から、これらのパラメーターの値に基づいて、制御システムが安定しているか、わずかに安定しているか、不安定であるかを判断できます。

• ゲインクロスオーバー周波数と位相クロスオーバー周波数
• ゲインマージンと位相マージン

位相クロスオーバー周波数

位相プロットは、-180の位相を有するされる周波数⁰として知られていますphase cross over frequency。それはによって示されます$\omega_{pc}$。位相クロスオーバー周波数の単位はrad/sec。

クロスオーバー周波数のゲイン

振幅プロットがゼロdBの振幅を持つ周波数は、次のように知られています。 gain cross over frequency。それはによって示されます$\omega_{gc}$。ゲインクロスオーバー周波数の単位はrad/sec。

位相クロスオーバー周波数とゲインクロスオーバー周波数の関係に基づく制御システムの安定性を以下に示します。

• 位相が周波数を超える場合 $\omega_{pc}$ ゲインクロスオーバー周波数よりも大きい $\omega_{gc}$、その後、制御システムは stable。

• 位相が周波数を超える場合 $\omega_{pc}$ ゲインクロスオーバー周波数に等しい $\omega_{gc}$、その後、制御システムは marginally stable。

• 位相が周波数を超える場合 $\omega_{pc}$ ゲインクロスオーバー周波数よりも小さい $\omega_{gc}$、その後、制御システムは unstable。

ゲインマージン

ゲインマージン $GM$ 位相クロスオーバー周波数でのdB単位の大きさの負の値に等しくなります。

$$GM=20\log\left( \frac{1}{M_{pc}}\right )=20logM_{pc}$$

どこ、 $M_{pc}$は、位相クロスオーバー周波数での大きさです。ゲインマージン（GM）の単位はdB。

位相マージン

位相マージンの式 $PM$ です

$$PM=180^0+\phi_{gc}$$

どこ、 $\phi_{gc}$は、ゲインクロスオーバー周波数での位相角です。位相余裕の単位はdegrees。

ゲインマージンと位相マージンの関係に基づく制御システムの安定性を以下に示します。

• 両方のゲインマージンの場合 $GM$ および位相マージン $PM$ が正の場合、制御システムは stable。

• 両方のゲインマージンの場合 $GM$ および位相マージン $PM$ がゼロに等しい場合、制御システムは marginally stable。

• ゲインマージンの場合 $GM$ および/または位相マージン $PM$ 負である/負である場合、制御システムは unstable。

前の章では、ボード線図について説明しました。そこでは、周波数の関数としての大きさと位相の両方について2つの別々のプロットがあります。ここで、極座標プロットについて説明します。極座標プロットは、大きさと位相の間に描くことができるプロットです。ここでは、大きさは通常の値のみで表されています。

の極形式 $G(j\omega)H(j\omega)$ です

$$G(j\omega)H(j\omega)=|G(j\omega)H(j\omega)| \angle G(j\omega)H(j\omega)$$

ザ・ Polar plot の大きさと位相角の間に描くことができるプロットです $G(j\omega)H(j\omega)$ 変化させることによって $\omega$ゼロから∞まで。極座標グラフシートを次の図に示します。

このグラフシートは、同心円と放射状の線で構成されています。ザ・concentric circles そしてその radial linesそれぞれ大きさと位相角を表します。これらの角度は、反時計回りの正の値で表されます。同様に、時計回りに負の値の角度を表すことができます。例えば、角度270 ⁰反時計回り方向には角度-90に等しく、⁰時計方向です。

極座標プロットを描画するためのルール

極座標プロットをプロットするには、次のルールに従ってください。

• 代替、 $s = j\omega$ 開ループ伝達関数で。

• の大きさと位相の式を書く $G(j\omega)H(j\omega)$。

• の開始振幅と位相を見つける $G(j\omega)H(j\omega)$ 代用することにより $\omega = 0$。したがって、極座標プロットは、この大きさと位相角から始まります。

• の終わりの大きさと位相を見つける $G(j\omega)H(j\omega)$ 代用することにより $\omega = \infty$。したがって、極座標プロットはこの大きさと位相角で終わります。

• の虚数項を作成して、極座標プロットが実軸と交差するかどうかを確認します。 $G(j\omega)H(j\omega)$ ゼロに等しく、の値を見つけます $\omega$。

• の実数項を作成して、極プロットが虚軸と交差するかどうかを確認します。 $G(j\omega)H(j\omega)$ ゼロに等しく、の値を見つけます $\omega$。

• 極座標プロットをより明確に描画するには、の大きさと位相を見つけます $G(j\omega)H(j\omega)$ の他の値を考慮することによって $\omega$。

例

閉ループ制御システムの開ループ伝達関数について考えてみます。

$$G(s)H(s)=\frac{5}{s(s+1)(s+2)}$$

上記のルールを使用して、この制御システムの極座標プロットを描画しましょう。

Step 1 −代用、 $s = j\omega$ 開ループ伝達関数で。

$$G(j\omega)H(j\omega)=\frac{5}{j\omega(j\omega+1)(j\omega+2)}$$

開ループ伝達関数の大きさは次のとおりです。

$$M=\frac{5}{\omega(\sqrt{\omega^2+1})(\sqrt{\omega^2+4})}$$

開ループ伝達関数の位相角は次のとおりです。

$$\phi=-90^0-\tan^{-1}\omega-\tan^{-1}\frac{\omega}{2}$$

Step 2 −次の表は、での開ループ伝達関数の大きさと位相角を示しています。 $\omega = 0$ ラジアン/秒および $\omega = \infty$ ラジアン/秒

周波数（ラジアン/秒）	マグニチュード	位相角（度）
0	∞	-90または270
∞	0	-270または90

したがって、極座標プロットは（∞、-90 ⁰）で始まり、（0、-270 ⁰）で終わり^ます。括弧内の第1項と第2項は、それぞれ大きさと位相角を示します。

Step 3−開始極座標と終了極座標に基づいて、この極プロットは負の実軸と交差します。負の実軸に対応する位相角が-180である⁰または180 ⁰。だから、-180のいずれかに開ループ伝達関数の位相角を等しくすることにより、⁰または180 ⁰、我々が得られます$\omega$ としての値 $\sqrt{2}$。

代用することにより $\omega = \sqrt{2}$ 開ループ伝達関数の大きさでは、次のようになります。 $M = 0.83$。したがって、極座標プロットは、次の場合に負の実軸と交差します。$\omega = \sqrt{2}$極座標は（0.83、−180 ⁰）です。

したがって、極座標グラフシートに上記の情報を使用して極座標プロットを描くことができます。

ナイキストプロットは、ωを-∞から∞まで変化させることによって閉ループ制御システムの安定性を見つけるための極座標プロットの続きです。つまり、ナイキストプロットを使用して、開ループ伝達関数の完全な周波数応答を描画します。

ナイキスト安定基準

ナイキスト安定基準は、 principle of argument。P極があり、Z零点が「s」平面の閉じたパスで囲まれている場合、対応する$G(s)H(s)$ 平面は原点を囲む必要があります $P − Z$回。したがって、包囲の数Nを次のように書くことができます。

$$N=P-Z$$

• 囲まれた「s」平面の閉じたパスに極のみが含まれている場合、 $G(s)H(s)$ 平面は、「s」平面で囲まれた閉じたパスの方向と反対になります。

• 囲まれた「s」平面の閉じたパスにゼロのみが含まれている場合、 $G(s)H(s)$ 平面は、「s」平面で囲まれた閉じたパスの方向と同じ方向になります。

ここで、偏角の原理を「s」平面の右半分全体に、閉じたパスとして選択して適用してみましょう。この選択されたパスは、Nyquist 輪郭。

閉ループ伝達関数のすべての極が「s」平面の左半分にある場合、閉ループ制御システムは安定していることがわかります。したがって、閉ループ伝達関数の極は、特性方程式の根に他なりません。特性方程式の次数が増えると、根を見つけるのが難しくなります。そこで、これらの特性方程式の根を次のように相関させましょう。

• 特性方程式の極は、開ループ伝達関数の極の極と同じです。

• 特性方程式の零点は、閉ループ伝達関数の極の零点と同じです。

's'平面の右半分に開ループ極がない場合、開ループ制御システムは安定していることがわかります。

すなわち、$P=0 \Rightarrow N=-Z$

's'平面の右半分に閉ループ極がない場合、閉ループ制御システムは安定していることがわかります。

すなわち、$Z=0 \Rightarrow N=P$

Nyquist stability criterion臨界点（1 + j0）の周りの円の数は、特性方程式の極に等しくなければならないと述べています。これは、「s」平面の右半分にある開ループ伝達関数の極に他なりません。原点を（1 + j0）にシフトすると、特性方程式の平面が得られます。

ナイキストプロットを描画するためのルール

ナイキストプロットをプロットするには、次のルールに従ってください。

• 開ループ伝達関数の極と零点を見つけます $G(s)H(s)$ 's'平面で。

• 変化させて極座標プロットを描く $\omega$ゼロから無限大まで。s = 0に極またはゼロが存在する場合、変化します$\omega$ 極座標プロットを描画するための0+から無限大まで。

• の値について、上記の極座標プロットの鏡像を描画します。 $\omega$−∞からゼロまでの範囲（0 ⁻ s = 0に極またはゼロが存在する場合）。

• 無限半径の半円の数は、原点の極またはゼロの数に等しくなります。無限半径の半円は、極座標プロットの鏡像が終了するポイントから始まります。そして、この無限半径の半円は、極プロットが始まるポイントで終了します。

ナイキストプロットを描いた後、ナイキスト安定基準を使用して閉ループ制御システムの安定性を見つけることができます。臨界点（-1 + j0）が円の外側にある場合、閉ループ制御システムは完全に安定しています。

ナイキストプロットを使用した安定性分析

ナイキストプロットから、これらのパラメーターの値に基づいて、制御システムが安定しているか、わずかに安定しているか、不安定であるかを識別できます。

• ゲインクロスオーバー周波数と位相クロスオーバー周波数
• ゲインマージンと位相マージン

位相クロスオーバー周波数

ナイキスト線図が負の実軸と交差する周波数（位相角は180 ⁰）は、phase cross over frequency。それはによって示されます$\omega_{pc}$。

クロスオーバー周波数のゲイン

ナイキスト線図が1の大きさを持つ頻度は、 gain cross over frequency。それはによって示されます$\omega_{gc}$。

位相クロスオーバー周波数とゲインクロスオーバー周波数の関係に基づく制御システムの安定性を以下に示します。

• 位相が周波数を超える場合 $\omega_{pc}$ ゲインクロスオーバー周波数よりも大きい $\omega_{gc}$、その後、制御システムは stable。

• 位相が周波数を超える場合 $\omega_{pc}$ ゲインクロスオーバー周波数に等しい $\omega_{gc}$、その後、制御システムは marginally stable。

• 位相が周波数を超える場合 $\omega_{pc}$ ゲインクロスオーバー周波数よりも小さい $\omega_{gc}$、その後、制御システムは unstable。

ゲインマージン

ゲインマージン $GM$ は、位相交差周波数でのナイキスト線図の大きさの逆数に等しくなります。

$$GM=\frac{1}{M_{pc}}$$

どこ、 $M_{pc}$ は、位相クロスオーバー周波数での通常のスケールでの大きさです。

位相マージン

位相マージン $PM$180の和に等しく、⁰および周波数にわたって利得クロスでの位相角。

$$PM=180^0+\phi_{gc}$$

どこ、 $\phi_{gc}$ は、ゲインクロスオーバー周波数での位相角です。

ゲインマージンと位相マージンの関係に基づく制御システムの安定性を以下に示します。

• ゲインマージンの場合 $GM$ が1より大きく、位相マージンが $PM$ が正の場合、制御システムは stable。

• ゲインマージンの場合 $GM$ 1に等しく、位相マージン $PM$ が0度の場合、制御システムは marginally stable。

• ゲインマージンの場合 $GM$ 1未満および/または位相マージン $PM$ が負の場合、制御システムは unstable。

補償器には、ラグ、リード、ラグリード補償器の3種類があります。これらは最も一般的に使用されます。

ラグ補償器

ラグ補償器は、正弦波入力が適用されたときに位相遅れを持つ正弦波出力を生成する電気ネットワークです。次の図に、「s」ドメインの遅れ補償回路を示します。

ここでは、コンデンサは抵抗と直列になっています $R_2$ そして、出力はこの組み合わせ全体で測定されます。

この遅れ補償器の伝達関数は-

$$\frac{V_o(s)}{V_i(s)}=\frac{1}{\alpha} \left( \frac{s+\frac{1}{\tau}}{s+\frac{1}{\alpha\tau}} \right )$$

どこ、

$$\tau=R_2C$$

$$\alpha=\frac{R_1+R_2}{R_2}$$

上記の式から、 $\alpha$ 常に1より大きい。

伝達関数から、遅れ補償器は次の場所に1つの極を持っていると結論付けることができます。 $s = − \frac{1}{\alpha \tau}$ と1つのゼロ $s = −\frac{1}{\tau}$。これは、ラグ補償器の極-零点構成では、極が原点に近くなることを意味します。

代替、 $s = j\omega$ 伝達関数で。

$$\frac{V_o(j\omega)}{V_i(j\omega)}=\frac{1}{\alpha}\left( \frac{j\omega+\frac{1}{\tau}}{j\omega+\frac{1}{\alpha\tau}}\right )$$

位相角 $\phi = \tan^{−1} \omega\tau − tan^{−1} \alpha\omega\tau$

出力正弦波信号の位相は、入力正弦波信号の位相角と伝達関数の合計に等しいことがわかっています。

したがって、この補償器の出力で位相遅れを生成するには、伝達関数の位相角を負にする必要があります。これは次の場合に発生します$\alpha > 1$。

リードコンペンセータ

リード補償器は、正弦波入力が適用されたときに位相リードを持つ正弦波出力を生成する電気ネットワークです。次の図に、「s」ドメインのリード補償回路を示します。

ここで、コンデンサは抵抗と並列です $R_1$ 出力は抵抗$ R_2の両端で測定されます。

この鉛補償器の伝達関数は-

$$ \ frac {V_o（s）} {V_i（s）} = \ beta \ left（\ frac {s \ tau + 1} {\ beta s \ tau + 1} \ right）$$

どこ、

$$ \ tau = R_1C $$

$$ \ beta = \ frac {R_2} {R_1 + R_2} $$

伝達関数から、鉛補償器は$ s = − \ frac {1} {\ beta}に極を持っていると結論付けることができます。$ and zero at $s = − \ frac {1} {\ beta \ tau} $。

伝達関数で$ s = j \ omega $に置き換えます。

$$ \ frac {V_o（j \ omega）} {V_i（j \ omega）} = \ beta \ left（\ frac {j \ omega \ tau + 1} {\ beta j \ omega \ tau + 1} \ right ）$$

位相角$ \ phi = tan ^ {-1} \ omega \ tau − tan ^ {-1} \ beta \ omega \ tau $

出力正弦波信号の位相は、入力正弦波信号の位相角と伝達関数の合計に等しいことがわかっています。

したがって、この補償器の出力で位相進みを生成するには、伝達関数の位相角が正である必要があります。これは、$ 0 <\ beta <1 $の場合に発生します。したがって、リード補償器の極-零点構成では、ゼロは原点に近くなります。

ラグリード補償器

ラグリード補償器は、1つの周波数領域で位相遅れを生成し、他の周波数領域で位相進みを生成する電気ネットワークです。これは、ラグ補償器とリード補償器の両方の組み合わせです。次の図に、「s」ドメインのラグリード補償回路を示します。

この回路は、両方の補償器がカスケード接続されているように見えます。したがって、この回路の伝達関数は、リード補償器とラグ補償器の伝達関数の積になります。

$$ \ frac {V_o（s）} {V_i（s）} = \ beta \ left（\ frac {s \ tau_1 + 1} {\ beta s \ tau_1 + 1} \ right）\ frac {1} {\ alpha} \ left（\ frac {s + \ frac {1} {\ tau_2}} {s + \ frac {1} {\ alpha \ tau_2}} \ right）$$

$ \ alpha \ beta = 1 $を知っています。

$$ \ Rightarrow \ frac {V_o（s）} {V_i（s）} = \ left（\ frac {s + \ frac {1} {\ tau_1}} {s + \ frac {1} {\ beta \ tau_1}} \ right）\ left（\ frac {s + \ frac {1} {\ tau_2}} {s + \ frac {1} {\ alpha \ tau_2}} \ right）$$

どこ、

$$ \ tau_1 = R_1C_1 $$

$$ \ tau_2 = R_2C_2 $$

制御システムのパフォーマンスを向上させるために、さまざまなタイプのコントローラーが使用されます。この章では、比例、微分、積分などの基本的なコントローラーについて説明します。

比例コントローラー

比例コントローラーは、エラー信号に比例する出力を生成します。

$$ u（t）\ propto e（t）$$

$$ \ Rightarrow u（t）= K_P e（t）$$

両側にラプラス変換を適用します-

$$ U（s）= K_P E（s）$$

$$ \ frac {U（s）} {E（s）} = K_P $$

したがって、比例コントローラーの伝達関数は$ K_P $です。

どこ、

U（s）は、作動信号u（t）のラプラス変換です。

E（s）は、エラー信号e（t）のラプラス変換です。

K _Pは比例定数であります

次の図に、ユニティネガティブフィードバック閉ループ制御システムと比例コントローラーのブロック図を示します。

比例コントローラーは、要件に従って過渡応答を変更するために使用されます。

微分コントローラー

微分コントローラーは、エラー信号の微分である出力を生成します。

$$ u（t）= K_D \ frac {\ text {d} e（t）} {\ text {d} t} $$

両側にラプラス変換を適用します。

$$ U（s）= K_D sE（s）$$

$$ \ frac {U（s）} {E（s）} = K_D s $$

したがって、微分コントローラーの伝達関数は$ K_D s $です。

ここで、$ K_D $は微分定数です。

次の図に、ユニティネガティブフィードバック閉ループ制御システムと微分コントローラーのブロック図を示します。

微分コントローラーは、不安定な制御システムを安定したものにするために使用されます。

一体型コントローラー

積分コントローラーは、エラー信号の積分である出力を生成します。

$$ u（t）= K_I \ int e（t）dt $$

両側にラプラス変換を適用します-

$$ U（s）= \ frac {K_I E（s）} {s} $$

$$ \ frac {U（s）} {E（s）} = \ frac {K_I} {s} $$

したがって、積分コントローラーの伝達関数は$ \ frac {K_I} {s} $です。

ここで、$ K_I $は整数定数です。

次の図に、ユニティネガティブフィードバック閉ループ制御システムと一体型コントローラーのブロック図を示します。

積分コントローラーは、定常状態の誤差を減らすために使用されます。

ここで、基本的なコントローラーの組み合わせについて説明します。

比例微分（PD）コントローラー

比例微分コントローラーは、比例コントローラーと微分コントローラーの出力の組み合わせである出力を生成します。

$$ u（t）= K_P e（t）+ K_D \ frac {\ text {d} e（t）} {\ text {d} t} $$

両側にラプラス変換を適用します-

$$ U（s）=（K_P + K_D s）E（s）$$

$$ \ frac {U（s）} {E（s）} = K_P + K_D s $$

したがって、比例微分コントローラーの伝達関数は$ K_P + K_D s $です。

次の図に、ユニティネガティブフィードバック閉ループ制御システムと比例微分コントローラーのブロック図を示します。

比例微分コントローラーは、定常状態の誤差に影響を与えることなく、制御システムの安定性を向上させるために使用されます。

比例積分（PI）コントローラー

比例積分コントローラーは、比例コントローラーと積分コントローラーの出力の組み合わせである出力を生成します。

$$ u（t）= K_P e（t）+ K_I \ int e（t）dt $$

両側にラプラス変換を適用します-

$$ U（s）= \ left（K_P + \ frac {K_I} {s} \ right）E（s）$$

$$ \ frac {U（s）} {E（s）} = K_P + \ frac {K_I} {s} $$

したがって、比例積分コントローラーの伝達関数は$ K_P + \ frac {K_I} {s} $です。

次の図に、ユニティネガティブフィードバック閉ループ制御システムと比例積分コントローラーのブロック図を示します。

比例積分コントローラーは、制御システムの安定性に影響を与えることなく、定常状態の誤差を減らすために使用されます。

比例積分微分（PID）コントローラー

比例積分微分コントローラーは、比例、積分、および微分コントローラーの出力の組み合わせである出力を生成します。

$$ u（t）= K_P e（t）+ K_I \ int e（t）dt + K_D \ frac {\ text {d} e（t）} {\ text {d} t} $$

両側にラプラス変換を適用します-

$$ U（s）= \ left（K_P + \ frac {K_I} {s} + K_D s \ right）E（s）$$

$$ \ frac {U（s）} {E（s）} = K_P + \ frac {K_I} {s} + K_D s $$

したがって、比例積分微分コントローラーの伝達関数は$ K_P + \ frac {K_I} {s} + K_D s $です。

次の図に、ユニティネガティブフィードバック閉ループ制御システムと比例積分微分コントローラーのブロック図を示します。

比例積分微分コントローラーは、制御システムの安定性を改善し、定常状態誤差を減らすために使用されます。

ザ・ state space model 線形時不変（LTI）システムのは、次のように表すことができます。

$$ \ dot {X} = AX + BU $$

$$ Y = CX + DU $$

1番目と2番目の方程式は、それぞれ状態方程式と出力方程式として知られています。

どこ、

• Xと$ \ dot {X} $は、それぞれ状態ベクトルと微分状態ベクトルです。

• UとYは、それぞれ入力ベクトルと出力ベクトルです。

• Aはシステム行列です。

• BとCは、入力行列と出力行列です。

• Dはフィードフォワード行列です。

状態空間モデルの基本概念

この章に含まれる次の基本的な用語。

状態

これは変数のグループであり、将来の値（出力）を予測するためにシステムの履歴を要約します。

状態変数

必要な状態変数の数は、システムに存在するストレージ要素の数と同じです。

Examples −インダクタを流れる電流、コンデンサ両端の電圧

状態ベクトル

これは、状態変数を要素として含むベクトルです。

前の章では、制御システムの2つの数学モデルについて説明しました。それらは微分方程式モデルと伝達関数モデルです。状態空間モデルは、これら2つの数学モデルのいずれかから取得できます。ここで、これら2つの方法を1つずつ説明します。

微分方程式からの状態空間モデル

次の一連のRLC回路について考えてみます。入力電圧$ v_i（t）があります$ and the current flowing through the circuit is $i（t）$。

この回路には2つのストレージ要素（インダクタとコンデンサ）があります。したがって、状態変数の数は2に等しく、これらの状態変数はインダクターを流れる電流$ i（t）です。$ and the voltage across capacitor, $v_c（t）$。

回路からの出力電圧$ v_0（t）$ is equal to the voltage across capacitor, $v_c（t）$。

$$ v_0（t）= v_c（t）$$

ループの周りにKVLを適用します。

$$ v_i（t）= Ri（t）+ L \ frac {\ text {d} i（t）} {\ text {d} t} + v_c（t）$$

$$ \ Rightarrow \ frac {\ text {d} i（t）} {\ text {d} t} =-\ frac {Ri（t）} {L}-\ frac {v_c（t）} {L} + \ frac {v_i（t）} {L} $$

コンデンサ両端の電圧は-

$$ v_c（t）= \ frac {1} {C} \ int i（t）dt $$

上記の方程式を時間で微分します。

$$ \ frac {\ text {d} v_c（t）} {\ text {d} t} = \ frac {i（t）} {C} $$

状態ベクトル、$ X = \ begin {bmatrix} i（t）\\ v_c（t）\ end {bmatrix} $

微分状態ベクトル、$ \ dot {X} = \ begin {bmatrix} \ frac {\ text {d} i（t）} {\ text {d} t} \\\ frac {\ text {d} v_c（t ）} {\ text {d} t} \ end {bmatrix} $

微分方程式と出力方程式を次のように状態空間モデルの標準形式に配置できます。

$$ \ dot {X} = \ begin {bmatrix} \ frac {\ text {d} i（t）} {\ text {d} t} \\\ frac {\ text {d} v_c（t）} { \ text {d} t} \ end {bmatrix} = \ begin {bmatrix}-\ frac {R} {L}＆-\ frac {1} {L} \\\ frac {1} {C}＆0 \ end {bmatrix} \ begin {bmatrix} i（t）\\ v_c（t）\ end {bmatrix} + \ begin {bmatrix} \ frac {1} {L} \\ 0 \ end {bmatrix} \ begin {bmatrix } v_i（t）\ end {bmatrix} $$

$$ Y = \ begin {bmatrix} 0＆1 \ end {bmatrix} \ begin {bmatrix} i（t）\\ v_c（t）\ end {bmatrix} $$

どこ、

$$ A = \ begin {bmatrix}-\ frac {R} {L}＆-\ frac {1} {L} \\\ frac {1} {C}＆0 \ end {bmatrix}、\：B = \ begin {bmatrix} \ frac {1} {L} \\ 0 \ end {bmatrix}、\：C = \ begin {bmatrix} 0＆1 \ end {bmatrix} \：および\：D = \ begin {bmatrix } 0 \ end {bmatrix} $$

伝達関数からの状態空間モデル

分子に存在する項のタイプに基づいて、2つのタイプの伝達関数を検討してください。

• 分子に定数項を持つ伝達関数。
• 分子の 's'の多項式関数を持つ伝達関数。

分子に定数項を持つ伝達関数

システムの次の伝達関数を考えてみましょう

$$ \ frac {Y（s）} {U（s）} = \ frac {b_0} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1s + a_0} $ $

上記の式を次のように並べ替えます

$$（s ^ n + a_ {n-1} s ^ {n-1} + ... + a_0）Y（s）= b_0 U（s）$$

両側に逆ラプラス変換を適用します。

$$ \ frac {\ text {d} ^ ny（t）} {\ text {d} t ^ n} + a_ {n-1} \ frac {\ text {d} ^ {n-1} y（t ）} {\ text {d} t ^ {n-1}} + ... + a_1 \ frac {\ text {d} y（t）} {\ text {d} t} + a_0y（t）= b_0 u（t）$$

しましょう

$$ y（t）= x_1 $$

$$ \ frac {\ text {d} y（t）} {\ text {d} t} = x_2 = \ dot {x} _1 $$

$$ \ frac {\ text {d} ^ 2y（t）} {\ text {d} t ^ 2} = x_3 = \ dot {x} _2 $$

$$。$$

$$。$$

$$。$$

$$ \ frac {\ text {d} ^ {n-1} y（t）} {\ text {d} t ^ {n-1}} = x_n = \ dot {x} _ {n-1} $ $

$$ \ frac {\ text {d} ^ ny（t）} {\ text {d} t ^ n} = \ dot {x} _n $$

および$ u（t）= u $

次に、

$$ \ dot {x} _n + a_ {n-1} x_n + ... + a_1x_2 + a_0x_1 = b_0 u $$

上記の式から、次の状態式を書くことができます。

$$ \ dot {x} _n = -a_0x_1-a_1x_2 -...- a_ {n-1} x_n + b_0 u $$

出力方程式は-

$$ y（t）= y = x_1 $$

状態空間モデルは-

$ \ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \\\ vdots \\\ dot {x} _ {n-1} \\\ dot {x} _n \ end {bmatrix} $

$$ = \ begin {bmatrix} 0＆1＆0＆\ dotso＆0＆0 \\ 0＆0＆1＆\ dotso＆0＆0 \\\ vdots＆\ vdots＆\ vdots＆\ dotso＆\ vdots ＆\ vdots \\ 0＆0＆0＆\ dotso＆0＆1 \\-a_0＆-a_1＆-a_2＆\ dotso＆-a_ {n-2}＆-a_ {n-1} \ end {bmatrix } \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} + \ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 0 \\ b_0 \ end {bmatrix} \ begin {bmatrix} u \ end {bmatrix} $$

$$ Y = \ begin {bmatrix} 1＆0＆\ dotso＆0＆0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} $$

ここで、$ D = \ left [0 \ right]。$

例

伝達関数を持つシステムの状態空間モデルを見つけます。

$$ \ frac {Y（s）} {U（s）} = \ frac {1} {s ^ 2 + s + 1} $$

上記の式を次のように並べ替えます。

$$（s ^ 2 + s + 1）Y（s）= U（s）$$

両側に逆ラプラス変換を適用します。

$$ \ frac {\ text {d} ^ 2y（t）} {\ text {d} t ^ 2} + \ frac {\ text {d} y（t）} {\ text {d} t} + y （t）= u（t）$$

しましょう

$$ y（t）= x_1 $$

$$ \ frac {\ text {d} y（t）} {\ text {d} t} = x_2 = \ dot {x} _1 $$

および$ u（t）= u $

すると、状態方程式は次のようになります。

$$ \ dot {x} _2 = -x_1-x_2 + u $$

出力方程式は次のとおりです。

$$ y（t）= y = x_1 $$

状態空間モデルは

$$ \ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} 0＆1 \\-1＆-1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 0 \\ 1 \ end {bmatrix} \ left [u \ right] $$

$$ Y = \ begin {bmatrix} 1＆0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} $$

分子内で 's'の多項式関数を持つ伝達関数

システムの次の伝達関数を考えてみましょう

$$ \ frac {Y（s）} {U（s）} = \ frac {b_n s ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0} $$

$$ \ Rightarrow \ frac {Y（s）} {U（s）} = \ left（\ frac {1} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0} \ right）（b_n s ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0）$$

上記の式は、カスケード接続された2つのブロックの伝達関数の積の形式です。

$$ \ frac {Y（s）} {U（s）} = \ left（\ frac {V（s）} {U（s）} \ right）\ left（\ frac {Y（s）} {V （s）} \ right）$$

ここに、

$$ \ frac {V（s）} {U（s）} = \ frac {1} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0} $$

上記の式を次のように並べ替えます

$$（s ^ n + a_ {n-1} s ^ {n-1} + ... + a_0）V（s）= U（s）$$

両側に逆ラプラス変換を適用します。

$$ \ frac {\ text {d} ^ nv（t）} {\ text {d} t ^ n} + a_ {n-1} \ frac {\ text {d} ^ {n-1} v（t ）} {\ text {d} t ^ {n-1}} + ... + a_1 \ frac {\ text {d} v（t）} {\ text {d} t} + a_0v（t）= u （t）$$

しましょう

$$ v（t）= x_1 $$

$$ \ frac {\ text {d} v（（t）} {\ text {d} t} = x_2 = \ dot {x} _1 $$

$$ \ frac {\ text {d} ^ 2v（t）} {\ text {d} t ^ 2} = x_3 = \ dot {x} _2 $$

$$。$$

$$。$$

$$。$$

$$ \ frac {\ text {d} ^ {n-1} v（t）} {\ text {d} t ^ {n-1}} = x_n = \ dot {x} _ {n-1} $ $

$$ \ frac {\ text {d} ^ nv（t）} {\ text {d} t ^ n} = \ dot {x} _n $$

および$ u（t）= u $

すると、状態方程式は次のようになります。

$$ \ dot {x} _n = -a_0x_1-a_1x_2 -...- a_ {n-1} x_n + u $$

考えてみてください

$$ \ frac {Y（s）} {V（s）} = b_ns ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0 $$

上記の式を次のように並べ替えます

$$ Y（s）=（b_ns ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0）V（s）$$

両側に逆ラプラス変換を適用します。

$$ y（t）= b_n \ frac {\ text {d} ^ nv（t）} {\ text {d} t ^ n} + b_ {n-1} \ frac {\ text {d} ^ {n -1} v（t）} {\ text {d} t ^ {n-1}} + ... + b_1 \ frac {\ text {d} v（t）} {\ text {d} t} + b_0v（t）$$

上記の方程式に状態変数と$ y（t）= y $を代入すると、出力方程式は次のようになります。

$$ y = b_n \ dot {x} _n + b_ {n-1} x_n + ... + b_1x_2 + b_0x_1 $$

上記の式の$ \ dot {x} _n $値を代入します。

$$ y = b_n（-a_0x_1-a_1x_2 -...- a_ {n-1} x_n + u）+ b_ {n-1} x_n + ... + b_1x_2 + b_0x_1 $$

$$ y =（b_0-b_na_0）x_1 +（b_1-b_na_1）x_2 + ... +（b_ {n-1} -b_na_ {n-1}）x_n + b_n u $$

状態空間モデルは

$ \ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \\\ vdots \\\ dot {x} _ {n-1} \\\ dot {x} _n \ end {bmatrix} $

$$ = \ begin {bmatrix} 0＆1＆0＆\ dotso＆0＆0 \\ 0＆0＆1＆\ dotso＆0＆0 \\\ vdots＆\ vdots＆\ vdots＆\ dotso＆\ vdots ＆\ vdots \\ 0＆0＆0＆\ dotso＆0＆1 \\-a_0＆-a_1＆-a_2＆\ dotso＆-a_ {n-2}＆-a_ {n-1} \ end {bmatrix } \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} + \ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 0 \\ b_0 \ end {bmatrix} \ begin {bmatrix} u \ end {bmatrix} $$

$$ Y = [b_0-b_na_0 \ quad b_1-b_na_1 \ quad ... \ quad b_ {n-2} -b_na_ {n-2} \ quad b_ {n-1} -b_na_ {n-1}] \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} $$

$ b_n = 0 $の場合、、

$$ Y = [b_0 \ quad b_1 \ quad ... \ quad b_ {n-2} \ quad b_ {n-1}] \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n- 1} \\ x_n \ end {bmatrix} $$

前の章では、微分方程式と伝達関数から状態空間モデルを取得する方法を学びました。この章では、状態空間モデルから伝達関数を取得する方法について説明します。

状態空間モデルからの伝達関数

線形時不変（LTI）システムの状態空間モデルは-

$$ \ dot {X} = AX + BU $$

$$ Y = CX + DU $$

状態方程式の両側にラプラス変換を適用します。

$$ sX（s）= AX（s）+ BU（s）$$

$$ \ Rightarrow（sI-A）X（s）= BU（s）$$

$$ \ Rightarrow X（s）=（sI-A）^ {-1} BU（s）$$

出力方程式の両側にラプラス変換を適用します。

$$ Y（s）= CX（s）+ DU（s）$$

上記の式のX（s）値を代入します。

$$ \ Rightarrow Y（s）= C（sI-A）^ {-1} BU（s）+ DU（s）$$

$$ \ Rightarrow Y（s）= [C（sI-A）^ {-1} B + D] U（s）$$

$$ \ Rightarrow \ frac {Y（s）} {U（s）} = C（sI-A）^ {-1} B + D $$

上記の式は、システムの伝達関数を表しています。したがって、状態空間モデルで表されるシステムに対してこの式を使用することにより、システムの伝達関数を計算できます。

Note − $ D = [0] $の場合、伝達関数は次のようになります。

$$ \ frac {Y（s）} {U（s）} = C（sI-A）^ {-1} B $$

Example

状態空間モデルで表されるシステムの伝達関数を次のように計算してみましょう。

$$ \ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} -1＆-1 \\ 1＆0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} [u] $$

$$ Y = \ begin {bmatrix} 0＆1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} $$

ここに、

$$ A = \ begin {bmatrix} -1＆-1 \\ 1＆0 \ end {bmatrix}、\ quad B = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix}、\ quad C = \ begin {bmatrix} 0＆1 \ end {bmatrix} \ quadおよび\ quad D = [0] $$

$ D = [0] $の場合の伝達関数の式は-

$$ \ frac {Y（s）} {U（s）} = C（sI-A）^ {-1} B $$

上記の式のA、B、C行列を代入します。

$$ \ frac {Y（s）} {U（s）} = \ begin {bmatrix} 0＆1 \ end {bmatrix} \ begin {bmatrix} s + 1＆1 \\-1＆s \ end {bmatrix } ^ {-1} \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} $$

$$ \ Rightarrow \ frac {Y（s）} {U（s）} = \ begin {bmatrix} 0＆1 \ end {bmatrix} \ frac {\ begin {bmatrix} s＆-1 \\ 1＆s + 1 \ end {bmatrix}} {（s + 1）s-1（-1）} \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} $$

$$ \ Rightarrow \ frac {Y（s）} {U（s）} = \ frac {\ begin {bmatrix} 0＆1 \ end {bmatrix} \ begin {bmatrix} s \\ 1 \ end {bmatrix}} {s ^ 2 + s + 1} = \ frac {1} {s ^ 2 + s + 1} $$

したがって、与えられた状態空間モデルに対するシステムの伝達関数は次のようになります。

$$ \ frac {Y（s）} {U（s）} = \ frac {1} {s ^ 2 + s + 1} $$

状態遷移マトリックスとそのプロパティ

システムに初期条件がある場合は、出力が生成されます。この出力は入力がなくても存在するため、zero input response$ x_ {ZIR}（t）$。数学的には、次のように書くことができます。

$$ x_ {ZIR}（t）= e ^ {At} X（0）= L ^ {-1} \ left \ {\ left [sI-A \ right] ^ {-1} X（0）\ right \} $$

上記の関係から、状態遷移行列$ \ phi（t）$を次のように書くことができます。

$$ \ phi（t）= e ^ {At} = L ^ {-1} [sI-A] ^ {-1} $$

したがって、ゼロ入力応答は、状態遷移行列$ \ phi（t）$に初期条件行列を乗算することで取得できます。

以下は、状態遷移行列のプロパティです。

• $ t = 0 $の場合、状態遷移行列は単位行列と等しくなります。

  $$ \ phi（0）= I $$

• 状態遷移行列の逆数は、「t」を「-t」に置き換えるだけで、状態遷移行列の逆数と同じになります。

  $$ \ phi ^ {-1}（t）= \ phi（−t）$$

• $ t = t_1 + t_2の場合$ , then the corresponding state transition matrix is equal to the multiplication of the two state transition matrices at $t = t_1$ and $t = t_2 $。

  $$ \ phi（t_1 + t_2）= \ phi（t_1）\ phi（t_2）$$

可制御性と可観測性

ここで、制御システムの制御性と可観測性について1つずつ説明します。

制御性

制御システムは controllable 制御システムの初期状態が、有限の時間内に制御された入力によって他のいくつかの望ましい状態に転送（変更）された場合。

を使用して制御システムの制御性を確認できます Kalman’s test。

• 行列$ Q_c $を次の形式で記述します。

  $$ Q_c = \ left [B \ quad AB \ quad A ^ 2B \ quad ... \ quad A ^ {n-1} B \ right] $$

• 行列$ Q_c $の行列式を見つけ、それがゼロに等しくない場合、制御システムは制御可能です。

可観測性

制御システムは observable 有限の時間内に出力を観察することにより、制御システムの初期状態を決定できるかどうか。

を使用して制御システムの可観測性を確認できます Kalman’s test。

• 行列$ Q_o $を次の形式で記述します。

  $$ Q_o = \ left [C ^ T \ quad A ^ TC ^ T \ quad（A ^ T）^ 2C ^ T \ quad ... \ quad（A ^ T）^ {n-1} C ^ T \右] $$

• 行列$ Q_o $の行列式を見つけ、それがゼロに等しくない場合、制御システムは観測可能です。

Example

状態空間モデルで次のように表される制御システムの制御可能性と可観測性を検証しましょう。

$$ \ dot {x} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} -1＆-1 \\ 1＆0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} [u] $$

$$ Y = \ begin {bmatrix} 0＆1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} $$

ここに、

$$ A = \ begin {bmatrix} -1＆-1 \\ 1＆0 \ end {bmatrix}、\ quad B = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix}、\ quad \ begin {bmatrix } 0＆1 \ end {bmatrix}、D = [0] \ quadおよび\ quad n = 2 $$

$ n = 2の場合$, the matrix $Q_c $は

$$ Q_c = \ left [B \ quad AB \ right] $$

行列AとBの積を次のように取得します。

$$ AB = \ begin {bmatrix} -1 \\ 1 \ end {bmatrix} $$

$$ \ Rightarrow Q_c = \ begin {bmatrix} 1＆-1 \\ 0＆1 \ end {bmatrix} $$

$$ | Q_c | = 1 \ neq 0 $$

行列$ Q_c $の行列式はゼロに等しくないため、与えられた制御システムは制御可能です。

$ n = 2の場合$, the matrix $Q_o $は-

$$ Q_o = \ left [C ^ T \ quad A ^ TC ^ T \ right] $$

ここに、

$$ A ^ T = \ begin {bmatrix} -1＆1 \\-1＆0 \ end {bmatrix} \ quadおよび\ quad C ^ T = \ begin {bmatrix} 0 \\ 1 \ end {bmatrix} $ $

行列$ A ^ Tの積を取得します$ and $C ^ T $ as

$$ A ^ TC ^ T = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} $$

$$ \ Rightarrow Q_o = \ begin {bmatrix} 0＆1 \\ 1＆0 \ end {bmatrix} $$

$$ \ Rightarrow | Q_o | = -1 \ quad \ neq 0 $$

行列$ Q_o $の行列式はゼロに等しくないため、与えられた制御システムは観測可能です。

したがって、特定の制御システムは制御可能であり、監視可能です。