一次システムの応答
この章では、一次システムの時間応答について説明します。次の閉ループ制御システムのブロック図を検討してください。ここでは、開ループ伝達関数$ \ frac {1} {sT} $が単一の負のフィードバックに接続されています。

閉ループ制御システムの伝達関数には、次のような単一の負のフィードバックがあることがわかっています。
$$ \ frac {C(s)} {R(s)} = \ frac {G(s)} {1 + G(s)} $$
上記の式に$ G(s)= \ frac {1} {sT} $を代入します。
$$ \ frac {C(s)} {R(s)} = \ frac {\ frac {1} {sT}} {1+ \ frac {1} {sT}} = \ frac {1} {sT + 1} $$
sの累乗は分母の項の1つです。したがって、上記の伝達関数は1次であり、システムは次のようになります。first order system。
上記の式を次のように書き直すことができます。
$$ C(s)= \ left(\ frac {1} {sT + 1} \ right)R(s)$$
どこ、
C(s) は出力信号c(t)のラプラス変換です。
R(s) は入力信号r(t)のラプラス変換であり、
T は時定数です。
次の手順に従って、時間領域で1次システムの応答(出力)を取得します。
入力信号$ r(t)$のラプラス変換を行います。
$ C(s)= \ left(\ frac {1} {sT + 1} \ right)R(s)$という方程式を考えてみましょう。
上記の式に$ R(s)$の値を代入します。
必要に応じて、$ C(s)$の部分分数を実行します。
逆ラプラス変換を$ C(s)$に適用します。
前の章では、インパルス、ステップ、ランプ、放物線などの標準的なテスト信号を見てきました。ここで、各入力に対する1次システムの応答を1つずつ調べてみましょう。応答の名前は、入力信号の名前に従って与えられます。たとえば、インパルス入力に対するシステムの応答は、インパルス応答と呼ばれます。
一次システムのインパルス応答
考えます unit impulse signal 一次システムへの入力として。
したがって、$ r(t)= \ delta(t)$
両側にラプラス変換を適用します。
$ R(s)= 1 $
$ C(s)= \ left(\ frac {1} {sT + 1} \ right)R(s)$という方程式を考えてみましょう。
上記の式で$ R(s)= 1 $を代入します。
$$ C(s)= \ left(\ frac {1} {sT + 1} \ right)(1)= \ frac {1} {sT + 1} $$
上記の方程式をラプラス変換の標準形式の1つに再配置します。
$$ C(s)= \ frac {1} {T \ left(\ s + \ frac {1} {T} \ right)} \ Rightarrow C(s)= \ frac {1} {T} \ left(\ frac {1} {s + \ frac {1} {T}} \ right)$$
両側に逆ラプラス変換を適用します。
$$ c(t)= \ frac {1} {T} e ^ \ left({-\ frac {t} {T}} \ right)u(t)$$
単位インパルス応答を次の図に示します。
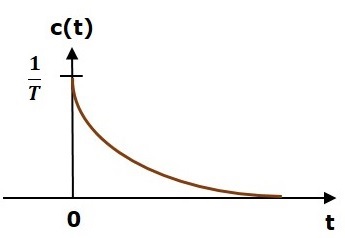
ザ・ unit impulse response、c(t)は、「t」の正の値の場合は指数関数的に減衰する信号であり、「t」の負の値の場合はゼロです。
一次システムのステップ応答
考えます unit step signal 一次システムへの入力として。
したがって、$ r(t)= u(t)$
両側にラプラス変換を適用します。
$$ R(s)= \ frac {1} {s} $$
$ C(s)= \ left(\ frac {1} {sT + 1} \ right)R(s)$という方程式を考えてみましょう。
上記の式に$ R(s)= \ frac {1} {s} $を代入します。
$$ C(s)= \ left(\ frac {1} {sT + 1} \ right)\ left(\ frac {1} {s} \ right)= \ frac {1} {s \ left(sT + 1 \ right)} $$
C(s)の部分分数を実行します。
$$ C(s)= \ frac {1} {s \ left(sT + 1 \ right)} = \ frac {A} {s} + \ frac {B} {sT + 1} $$
$$ \ Rightarrow \ frac {1} {s \ left(sT + 1 \ right)} = \ frac {A \ left(sT + 1 \ right)+ Bs} {s \ left(sT + 1 \ right)} $$
どちらの側でも、分母の項は同じです。だから、彼らはお互いにキャンセルされます。したがって、分子の項を等しくします。
$$ 1 = A \ left(sT + 1 \ right)+ Bs $$
両側の定数項を等しくすることにより、A = 1が得られます。
代入、A = 1、の係数を等しくします s 両側の用語。
$$ 0 = T + B \ Rightarrow B = -T $$
$ C(s)$の部分分数展開で、A = 1およびB = −Tに置き換えます。
$$ C(s)= \ frac {1} {s}-\ frac {T} {sT + 1} = \ frac {1} {s}-\ frac {T} {T \ left(s + \ frac { 1} {T} \ right)} $$
$$ \ Rightarrow C(s)= \ frac {1} {s}-\ frac {1} {s + \ frac {1} {T}} $$
両側に逆ラプラス変換を適用します。
$$ c(t)= \ left(1-e ^ {-\ left(\ frac {t} {T} \ right)} \ right)u(t)$$
ザ・ unit step response、c(t)には、過渡状態と定常状態の両方の項があります。
単位ステップ応答の過渡項は-
$$ c_ {tr}(t)=-e ^ {-\ left(\ frac {t} {T} \ right)} u(t)$$
単位ステップ応答の定常状態の項は-
$$ c_ {ss}(t)= u(t)$$
次の図は、単位ステップ応答を示しています。

の値 unit step response, c(t)t = 0で、tのすべての負の値に対してゼロです。ゼロ値から徐々に増加し、最終的に定常状態で1に達します。したがって、定常状態の値は入力の大きさに依存します。
一次システムのランプ応答
考えます unit ramp signal 一次システムへの入力として。
$だから、r(t)= tu(t)$
両側にラプラス変換を適用します。
$$ R(s)= \ frac {1} {s ^ 2} $$
$ C(s)= \ left(\ frac {1} {sT + 1} \ right)R(s)$という方程式を考えてみましょう。
上記の式に$ R(s)= \ frac {1} {s ^ 2} $を代入します。
$$ C(s)= \ left(\ frac {1} {sT + 1} \ right)\ left(\ frac {1} {s ^ 2} \ right)= \ frac {1} {s ^ 2( sT + 1)} $$
$ C(s)$の部分分数を実行します。
$$ C(s)= \ frac {1} {s ^ 2(sT + 1)} = \ frac {A} {s ^ 2} + \ frac {B} {s} + \ frac {C} {sT +1} $$
$$ \ Rightarrow \ frac {1} {s ^ 2(sT + 1)} = \ frac {A(sT + 1)+ Bs(sT + 1)+ Cs ^ 2} {s ^ 2(sT + 1) } $$
どちらの側でも、分母の項は同じです。だから、彼らはお互いにキャンセルされます。したがって、分子の項を等しくします。
$$ 1 = A(sT + 1)+ Bs(sT + 1)+ Cs ^ 2 $$
両側の定数項を等しくすることにより、A = 1が得られます。
A = 1に置き換えて、両側のs項の係数を等しくします。
$$ 0 = T + B \ Rightarrow B = -T $$
同様に、B = −Tに置き換えて、両側の$ s ^ 2 $項の係数を等しくします。$ C = T ^ 2 $を取得します。
$ C(s)$の部分分数展開で、A = 1、B = −T、および$ C = T ^ 2 $を代入します。
$$ C(s)= \ frac {1} {s ^ 2}-\ frac {T} {s} + \ frac {T ^ 2} {sT + 1} = \ frac {1} {s ^ 2} -\ frac {T} {s} + \ frac {T ^ 2} {T \ left(s + \ frac {1} {T} \ right)} $$
$$ \ Rightarrow C(s)= \ frac {1} {s ^ 2}-\ frac {T} {s} + \ frac {T} {s + \ frac {1} {T}} $$
両側に逆ラプラス変換を適用します。
$$ c(t)= \ left(t-T + Te ^ {-\ left(\ frac {t} {T} \ right)} \ right)u(t)$$
ザ・ unit ramp response、c(t)には、過渡状態と定常状態の両方の項があります。
ユニットランプ応答の過渡項は-
$$ c_ {tr}(t)= Te ^ {-\ left(\ frac {t} {T} \ right)} u(t)$$
ユニットランプ応答の定常状態の項は-
$$ c_ {ss}(t)=(tT)u(t)$$
次の図は、ユニットランプ応答を示しています。

ザ・ unit ramp response、c(t)は、tのすべての正の値に対してユニットランプ入力信号に従います。ただし、入力信号からT単位の偏差があります。
一次システムの放物線応答
考えます unit parabolic signal 一次システムへの入力として。
したがって、$ r(t)= \ frac {t ^ 2} {2} u(t)$
両側にラプラス変換を適用します。
$$ R(s)= \ frac {1} {s ^ 3} $$
$ C(s)= \ left(\ frac {1} {sT + 1} \ right)R(s)$という方程式を考えてみましょう。
上記の式に$ R(s)= \ frac {1} {s ^ 3} $を代入します。
$$ C(s)= \ left(\ frac {1} {sT + 1} \ right)\ left(\ frac {1} {s ^ 3} \ right)= \ frac {1} {s ^ 3( sT + 1)} $$
$ C(s)$の部分分数を実行します。
$$ C(s)= \ frac {1} {s ^ 3(sT + 1)} = \ frac {A} {s ^ 3} + \ frac {B} {s ^ 2} + \ frac {C} {s} + \ frac {D} {sT + 1} $$
単純化すると、A、B、C、およびDの値がそれぞれ1、$-T、\:T ^ 2 \ :、および\:− T ^ 3 $として取得されます。これらの値を上記のC(s)の部分分数展開に代入します。
$ C(s)= \ frac {1} {s ^ 3}-\ frac {T} {s ^ 2} + \ frac {T ^ 2} {s}-\ frac {T ^ 3} {sT + 1 } \:\ Rightarrow C(s)= \ frac {1} {s ^ 3}-\ frac {T} {s ^ 2} + \ frac {T ^ 2} {s}-\ frac {T ^ 2} {s + \ frac {1} {T}} $
両側に逆ラプラス変換を適用します。
$$ c(t)= \ left(\ frac {t ^ 2} {2} -Tt + T ^ 2-T ^ 2e ^ {-\ left(\ frac {t} {T} \ right)} \ right )u(t)$$
ザ・ unit parabolic response、c(t)には、過渡状態と定常状態の両方の項があります。
単位放物線応答の過渡項は次のとおりです。
$$ C_ {tr}(t)=-T ^ 2e ^ {-\ left(\ frac {t} {T} \ right)} u(t)$$
単位放物線応答の定常状態の項は次のとおりです。
$$ C_ {ss}(t)= \ left(\ frac {t ^ 2} {2} -Tt + T ^ 2 \ right)u(t)$$
これらの応答から、これらの応答は無限の時間でも増加し続けるため、一次制御システムはランプおよび放物線入力では安定していないと結論付けることができます。一次制御システムは、これらの応答が出力を制限しているため、インパルス入力とステップ入力で安定しています。ただし、インパルス応答には定常状態の項がありません。そのため、ステップ信号は、応答から制御システムを分析するために時間領域で広く使用されています。