DSP - быстрое преобразование Фурье
В более ранних методах ДПФ мы видели, что вычислительная часть слишком длинная. Мы хотим уменьшить это. Это можно сделать с помощью БПФ или быстрого преобразования Фурье. Итак, мы можем сказать, что БПФ - это не что иное, как вычисление дискретного преобразования Фурье в алгоритмическом формате, в котором вычислительная часть будет сокращена.
Основное преимущество БПФ заключается в том, что с его помощью мы можем создавать КИХ-фильтры. Математически БПФ можно записать следующим образом;
$$ x [K] = \ displaystyle \ sum \ limits_ {n = 0} ^ {N-1} x [n] W_N ^ {nk} $$Давайте рассмотрим пример, чтобы лучше понять это. Мы рассмотрели восемь точек с названиями от $ x_0 \ quad до \ quad x_7 $. Мы выберем четные члены в одной группе и нечетные - в другой. Схематический вид вышесказанного показан ниже -
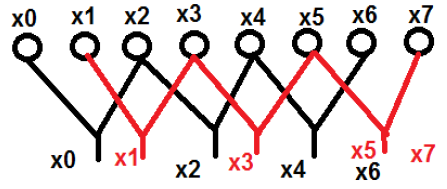
Здесь точки x 0 , x 2 , x 4 и x 6 были сгруппированы в одну категорию, и аналогично точки x 1 , x 3 , x 5 и x 7 были помещены в другую категорию. Теперь мы можем объединить их в группу из двух и продолжить вычисления. Теперь давайте посмотрим, как это разбиение на еще два помогает в вычислениях.
$ Икс [К] = \ Displaystyle \ сумма \ limits_ {r = 0} ^ {\ гидроразрыва {N} {2} -1} x [2r] W_N ^ {2rk} + \ displaystyle \ sum \ limits_ {r = 0 } ^ {\ frac {N} {2} -1} x [2r + 1] W_N ^ {(2r + 1) k} $
$ = \ sum_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_ {N / 2} ^ {rk} + \ sum_ {r = 0} ^ {\ frac {N } {2} -1} x [2r + 1] W_ {N / 2} ^ {rk} \ times W_N ^ k $
$ = G [k] + H [k] \ times W_N ^ k $
Изначально мы взяли последовательность из восьми точек, но позже мы разбили ее на две части G [k] и H [k]. G [k] обозначает четную часть, а H [k] обозначает нечетную часть. Если мы хотим реализовать это с помощью диаграммы, то это можно показать, как показано ниже -
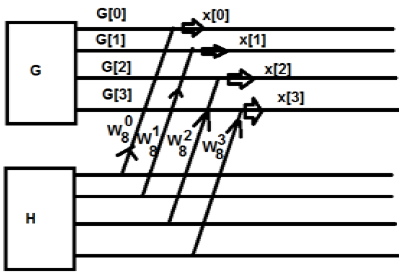
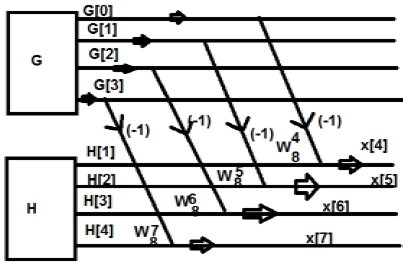
Из рисунка выше видно, что
$ W_8 ^ 4 = -1 $
$ W_8 ^ 5 = -W_8 ^ 1 $
$ W_8 ^ 6 = -W_8 ^ 2 $
$ W_8 ^ 7 = -W_8 ^ 3 $
Точно так же окончательные значения могут быть записаны следующим образом -
$ G [0] -H [0] = x [4] $
$ G [1] -W_8 ^ 1H [1] = x [5] $
$ G [2] -W_8 ^ 2H [2] = x [6] $
$ G [1] -W_8 ^ 3H [3] = x [7] $
Вышеупомянутый - периодический ряд. Недостатком этой системы является то, что K нельзя превысить 4 балла. Теперь давайте разберем вышесказанное на более мелкие. Получим конструкции примерно такие
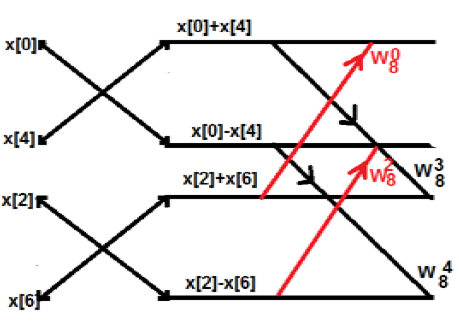
пример
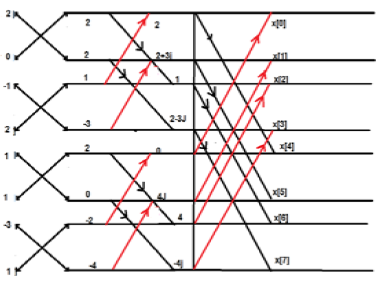
Рассмотрим последовательность x [n] = {2,1, -1, -3,0,1,2,1}. Рассчитайте БПФ.
Solution - Данная последовательность x [n] = {2,1, -1, -3,0,1,2,1}
Расположите условия, как показано ниже;