DSP - Операции по интеграции сигналов
Интеграция любого сигнала означает суммирование этого сигнала в определенной временной области для получения модифицированного сигнала. Математически это можно представить как -
$$ x (t) \ rightarrow y (t) = \ int _ {- \ infty} ^ {t} x (t) dt $$Здесь также в большинстве случаев мы можем выполнить математическое интегрирование и найти результирующий сигнал, но прямое интегрирование в быстрой последовательности возможно для сигналов, которые графически изображены в прямоугольном формате. Как и в случае дифференциации, здесь мы также обратимся к таблице, чтобы быстро получить результат.
| Исходный сигнал | Интегрированный сигнал |
|---|---|
| 1 | импульс |
| Импульс | шаг |
| Шаг | Рампа |
пример
Рассмотрим сигнал $ x (t) = u (t) -u (t-3) $. Это показано на рисунке 1 ниже. Ясно, что это ступенчатый сигнал. Теперь интегрируем. Обращаясь к таблице, мы знаем, что интегрирование ступенчатого сигнала дает линейный сигнал.
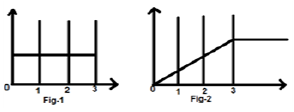
Однако мы рассчитаем это математически,
$ y (t) = \ int _ {- \ infty} ^ {t} x (t) dt $
$ = \ int _ {- \ infty} ^ {t} [u (t) -u (t-3)] dt $
$ = \ int _ {- \ infty} ^ {t} u (t) dt- \ int _ {- \ infty} ^ {t} u (t-3) dt $
$ = r (t) -r (t-3) $
То же, что и на рис. 2,