DSP - вычисление на месте
Это эффективное использование памяти важно для разработки быстрого оборудования для вычисления БПФ. Термин «вычисление на месте» используется для описания этого использования памяти.
Прореживание во временной последовательности
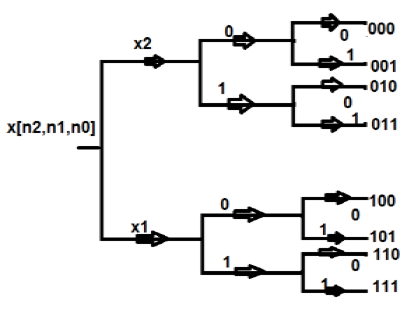
В этой структуре мы представляем все точки в двоичном формате, то есть в 0 и 1. Затем мы меняем эти структуры на противоположные. Последовательность, которую мы получаем после этого, называется последовательностью обращения битов. Это также известно как прореживание во временной последовательности. Вычисление на месте восьмиточечного ДПФ показано в табличном формате, как показано ниже -
| ТОЧКИ | ДВОИЧНЫЙ ФОРМАТ | ОБРАТНЫЙ | ЭКВИВАЛЕНТНЫЕ ТОЧКИ |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
Прореживание в частотной последовательности
Помимо временной последовательности, последовательность из N точек также может быть представлена по частоте. Давайте возьмем последовательность из четырех пунктов, чтобы лучше ее понять.
Пусть последовательность будет $ x [0], x [1], x [2], x [3], x [4], x [5], x [6], x [7] $. Сначала мы сгруппируем две точки в одну группу. Математически эту последовательность можно записать как;
$$ x [k] = \ sum_ {n = 0} ^ {N-1} x [n] W_N ^ {nk} $$Теперь давайте создадим одну группу с порядковыми номерами от 0 до 3, а другую группу с последовательностями с 4 по 7. Теперь математически это можно представить как;
$$ \ displaystyle \ sum \ limits_ {n = 0} ^ {\ frac {N} {2} -1} x [n] W_N ^ {nk} + \ displaystyle \ sum \ limits_ {n = N / 2} ^ {N-1} x [n] W_N ^ {nk} $$Заменим n на r, где r = 0, 1, 2…. (N / 2-1). Математически,
$$ \ displaystyle \ sum \ limits_ {n = 0} ^ {\ frac {N} {2} -1} x [r] W_ {N / 2} ^ {nr} $$Сначала мы берем первые четыре точки (x [0], x [1], x [2], x [3]) и пытаемся представить их математически следующим образом:
$ \ sum_ {n = 0} ^ 3x [n] W_8 ^ {nk} + \ sum_ {n = 0} ^ 3x [n + 4] W_8 ^ {(n + 4) k} $
$ = \ lbrace \ sum_ {n = 0} ^ 3x [n] + \ sum_ {n = 0} ^ 3x [n + 4] W_8 ^ {(4) k} \ rbrace \ times W_8 ^ {nk} $
теперь $ X [0] = \ sum_ {n = 0} ^ 3 (X [n] + X [n + 4]) $
$ X [1] = \ sum_ {n = 0} ^ 3 (X [n] + X [n + 4]) W_8 ^ {nk} $
$ = [X [0] -X [4] + (X [1] -X [5]) W_8 ^ 1 + (X [2] -X [6]]) W_8 ^ 2 + (X [3] -X [7]) W_8 ^ 3 $
Далее мы можем разбить его еще на две части, что означает, что вместо того, чтобы разбивать их на последовательность из 4 пунктов, мы можем разбить их на последовательность из 2 пунктов.