제어 시스템-블록 다이어그램

블록 다이어그램은 단일 블록 또는 블록 조합으로 구성됩니다. 이들은 제어 시스템을 그림 형식으로 표현하는 데 사용됩니다.

블록 다이어그램의 기본 요소

블록 다이어그램의 기본 요소는 블록, 합산 지점 및 이륙 지점입니다. 이러한 요소를 식별하기 위해 다음 그림에 표시된 폐 루프 제어 시스템의 블록 다이어그램을 고려해 보겠습니다.

위의 블록 다이어그램은 전달 함수 G (s)와 H (s)가있는 두 개의 블록으로 구성됩니다. 또한 하나의 합산 지점과 하나의 이륙 지점이 있습니다. 화살표는 신호 흐름의 방향을 나타냅니다. 이제 이러한 요소를 하나씩 논의하겠습니다.

블록

구성 요소의 전달 함수는 블록으로 표시됩니다. 블록에는 단일 입력 및 단일 출력이 있습니다.

다음 그림은 입력 X (s), 출력 Y (s) 및 전달 함수 G (s)가있는 블록을 보여줍니다.

전달 함수, $ G (s) = \ frac {Y (s)} {X (s)} $

$$ \ 오른쪽 화살표 Y (s) = G (s) X (s) $$

블록의 출력은 블록의 전달 함수를 입력과 곱하여 얻습니다.

합산 점

합산 점은 내부에 십자 (X)가있는 원으로 표시됩니다. 두 개 이상의 입력과 단일 출력이 있습니다. 입력의 대수 합계를 생성합니다. 또한 입력의 극성을 기반으로 입력의 합산 또는 빼기 또는 합산 및 빼기 조합을 수행합니다. 이 세 가지 작업을 하나씩 살펴 보겠습니다.

다음 그림은 두 개의 입력 (A, B)과 하나의 출력 (Y)이있는 합산 지점을 보여줍니다. 여기에서 입력 A와 B는 양의 부호를 갖습니다. 따라서 합산 점은 출력 Y를 다음과 같이 생성합니다.sum of A and B.

즉, Y = A + B.

다음 그림은 두 개의 입력 (A, B)과 하나의 출력 (Y)이있는 합산 지점을 보여줍니다. 여기에서 입력 A와 B는 반대 부호를 가지고 있습니다. 즉, A는 양수 부호이고 B는 음수 부호입니다. 따라서 합산 점은 출력을 생성합니다.Y 로 difference of A and B.

Y = A + (-B) = A-B.

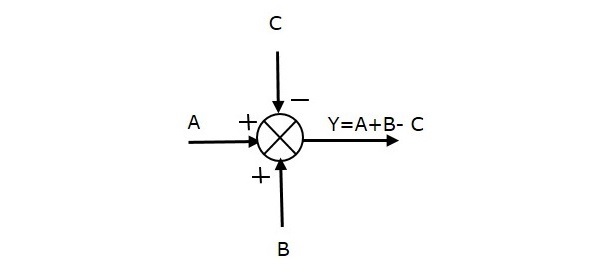
다음 그림은 3 개의 입력 (A, B, C)과 1 개의 출력 (Y)이있는 합산 지점을 보여줍니다. 여기에서 입력 A와 B는 양수 부호이고 C는 음수 부호입니다. 따라서 합산 점은 출력을 생성합니다.Y 같이

Y = A + B + (−C) = A + B − C.

이륙 지점

이륙 지점은 동일한 입력 신호가 둘 이상의 분기를 통과 할 수있는 지점입니다. 즉, 이륙 지점의 도움으로 동일한 입력을 하나 이상의 블록, 합산 지점에 적용 할 수 있습니다.

다음 그림에서 이륙 지점은 동일한 입력 R (s)를 두 개의 추가 블록에 연결하는 데 사용됩니다.

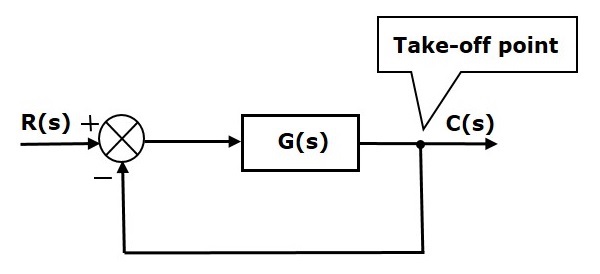
다음 그림에서 이륙 지점은 합산 지점에 대한 입력 중 하나로 출력 C (s)를 연결하는 데 사용됩니다.

전기 시스템의 블록 다이어그램 표현

이 섹션에서는 블록 다이어그램으로 전기 시스템을 표현해 보겠습니다. 전기 시스템은 주로 세 가지 기본 요소를 포함합니다.resistor, inductor and capacitor.

다음 그림과 같이 일련의 RLC 회로를 고려하십시오. 여기서 V _i (t) 및 V _o (t)는 입력 및 출력 전압입니다. i (t)를 회로를 통과하는 전류라고합시다. 이 회로는 시간 영역에 있습니다.

이 회로에 Laplace 변환을 적용하면 s 도메인의 회로를 얻을 수 있습니다. 회로는 다음 그림과 같습니다.

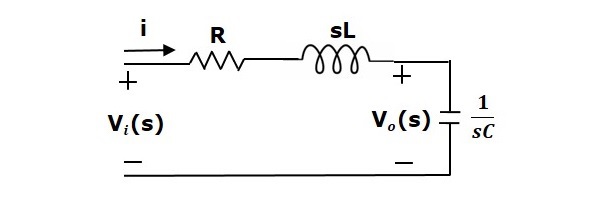
위의 회로에서 다음과 같이 쓸 수 있습니다.

$$ I (s) = \ frac {V_i (s) -V_o (s)} {R + sL} $$

$ \ Rightarrow I (s) = \ left \ {\ frac {1} {R + sL} \ right \} \ left \ {V_i (s) -V_o (s) \ right \} $ (Equation 1)

$ V_o (s) = \ left (\ frac {1} {sC} \ right) I (s) $ (Equation 2)

이제이 두 방정식에 대한 블록 다이어그램을 개별적으로 그려 보겠습니다. 그런 다음 일련의 RLC 회로 (s- 도메인)의 전체 블록 다이어그램을 얻기 위해 이러한 블록 다이어그램을 적절하게 결합합니다.

방정식 1은 전달 함수 $ \ frac {1} {R + sL} $를 갖는 블록으로 구현 될 수 있습니다. 이 블록의 입력 및 출력은 $ \ left \ {V_i (s) -V_o (s) \ right \} $ 및 $ I (s) $입니다. $ \ left \ {V_i (s) -V_o (s) \ right \} $를 얻으려면 합산 점이 필요합니다. 방정식 1의 블록 다이어그램은 다음 그림에 나와 있습니다.