제어 시스템-퀵 가이드

제어 시스템은 출력을 제어하여 원하는 응답을 제공하는 시스템입니다. 다음 그림은 제어 시스템의 간단한 블록 다이어그램을 보여줍니다.

여기서 제어 시스템은 단일 블록으로 표시됩니다. 출력은 다양한 입력으로 제어되기 때문에 제어 시스템이이 이름을 얻었습니다. 이 입력을 몇 가지 메커니즘으로 변경합니다. 개방 루프 및 폐쇄 루프 제어 시스템에 대한 다음 섹션에서는 제어 시스템 내부의 블록과 원하는 응답을 얻기 위해이 입력을 변경하는 방법에 대해 자세히 알아 봅니다.

Examples − 신호등 제어 시스템, 세탁기

Traffic lights control system제어 시스템의 예입니다. 여기에서 일련의 입력 신호가이 제어 시스템에 적용되고 출력은 일정 시간 동안 켜질 세 개의 표시 등 중 하나입니다. 이 시간 동안 다른 두 개의 표시등이 꺼집니다. 특정 교차로의 교통 조사를 기반으로 조명의 켜짐 및 꺼짐 시간을 결정할 수 있습니다. 따라서 입력 신호가 출력을 제어합니다. 따라서 신호등 제어 시스템은 시간 기준으로 작동합니다.

제어 시스템의 분류

일부 매개 변수를 기반으로 제어 시스템을 다음과 같은 방식으로 분류 할 수 있습니다.

연속 시간 및 이산 시간 제어 시스템

• 제어 시스템은 연속 시간 제어 시스템과 이산 시간 제어 시스템으로 분류 할 수 있습니다. type of the signal 익숙한.

• 에 continuous time제어 시스템, 모든 신호는 시간에 연속적입니다. 하지만discrete time 제어 시스템에는 하나 이상의 이산 시간 신호가 있습니다.

SISO 및 MIMO 제어 시스템

• 제어 시스템은 SISO 제어 시스템과 MIMO 제어 시스템으로 분류 할 수 있습니다. number of inputs and outputs 선물.

• SISO(단일 입력 및 단일 출력) 제어 시스템에는 하나의 입력과 하나의 출력이 있습니다. 이므로,MIMO (다중 입력 및 다중 출력) 제어 시스템에는 하나 이상의 입력과 하나 이상의 출력이 있습니다.

개방 루프 및 폐쇄 루프 제어 시스템

제어 시스템은 개방형 루프 제어 시스템과 폐쇄 형 루프 제어 시스템으로 분류 할 수 있습니다. feedback path.

에 open loop control systems, 출력이 입력으로 피드백되지 않습니다. 따라서 제어 동작은 원하는 출력과 무관합니다.

다음 그림은 개방 루프 제어 시스템의 블록 다이어그램을 보여줍니다.

여기에서 입력은 컨트롤러에 적용되어 작동 신호 또는 제어 신호를 생성합니다. 이 신호는 제어 할 플랜트 또는 프로세스에 대한 입력으로 제공됩니다. 따라서 공장은 제어되는 출력을 생산합니다. 앞에서 논의한 신호등 제어 시스템은 개방 루프 제어 시스템의 예입니다.

에 closed loop control systems, 출력이 입력으로 피드백됩니다. 따라서 제어 동작은 원하는 출력에 따라 다릅니다.

다음 그림은 네거티브 피드백 폐쇄 루프 제어 시스템의 블록 다이어그램을 보여줍니다.

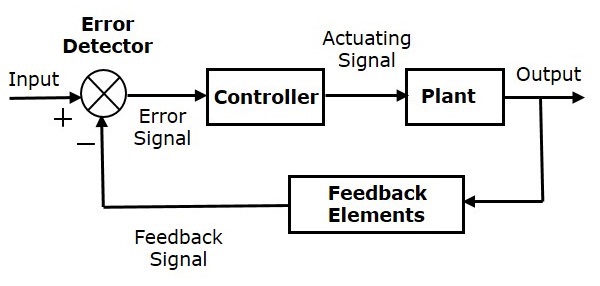
오류 감지기는 입력 신호와 피드백 신호의 차이 인 오류 신호를 생성합니다. 이 피드백 신호는 전체 시스템의 출력을이 블록에 대한 입력으로 고려하여 블록 (피드백 요소)에서 얻습니다. 직접 입력 대신 오류 신호가 컨트롤러에 대한 입력으로 적용됩니다.

따라서 컨트롤러는 플랜트를 제어하는 ​​작동 신호를 생성합니다. 이 조합에서 제어 시스템의 출력은 원하는 응답을 얻을 때까지 자동으로 조정됩니다. 따라서 폐쇄 루프 제어 시스템을 자동 제어 시스템이라고도합니다. 입력에 센서가있는 신호등 제어 시스템은 폐쇄 루프 제어 시스템의 예입니다.

개방 루프와 폐쇄 루프 제어 시스템의 차이점은 다음 표에 나와 있습니다.

개방형 루프 제어 시스템	폐쇄 루프 제어 시스템
제어 동작은 원하는 출력과 무관합니다.	제어 동작은 원하는 출력에 따라 다릅니다.
피드백 경로가 없습니다.	피드백 경로가 있습니다.
이것들은 또한 non-feedback control systems.	이것들은 또한 feedback control systems.
디자인하기 쉽습니다.	디자인하기 어렵습니다.
경제적입니다.	비용이 많이 듭니다.
정확하지 않습니다.	정확한.

출력 또는 출력의 일부가 입력 측으로 반환되어 시스템 입력의 일부로 활용되면 다음과 같이 알려져 있습니다. feedback. 피드백은 제어 시스템의 성능을 향상시키는 데 중요한 역할을합니다. 이 장에서는 피드백의 유형과 피드백의 효과에 대해 논의하겠습니다.

피드백 유형

피드백에는 두 가지 유형이 있습니다.

• 긍정적 인 피드백
• 부정적인 의견

긍정적 인 피드백

긍정적 인 피드백은 참조 입력을 추가합니다. $R(s)$및 피드백 출력. 다음 그림은 블록 다이어그램을 보여줍니다.positive feedback control system.

전달 함수의 개념은 이후 장에서 설명합니다. 당분간 포지티브 피드백 제어 시스템의 전달 함수는 다음과 같습니다.

$T=\frac{G}{1-GH}$ (수식 1)

어디,

• T 전달 함수 또는 포지티브 피드백 제어 시스템의 전체 이득입니다.

• G 주파수의 함수 인 개방 루프 이득입니다.

• H 주파수의 함수 인 피드백 경로의 이득입니다.

부정적인 의견

네거티브 피드백은 레퍼런스 입력 사이의 오류를 줄입니다. $R(s)$및 시스템 출력. 다음 그림은negative feedback control system.

네거티브 피드백 제어 시스템의 전달 함수는 다음과 같습니다.

$T=\frac{G}{1+GH}$ (수식 2)

어디,

• T 네거티브 피드백 제어 시스템의 전달 함수 또는 전체 이득입니다.

• G 주파수의 함수 인 개방 루프 이득입니다.

• H 주파수의 함수 인 피드백 경로의 이득입니다.

위의 전달 함수의 파생은 이후 장에 있습니다.

피드백의 효과

이제 피드백의 효과를 이해하겠습니다.

피드백이 전체 이득에 미치는 영향

• 방정식 2에서 네거티브 피드백 폐쇄 루프 제어 시스템의 전체 이득은 'G'와 (1 + GH)의 비율이라고 말할 수 있습니다. 따라서 전체 이득은 (1 + GH)의 값에 따라 증가하거나 감소 할 수 있습니다.

• (1 + GH)의 값이 1보다 작 으면 전체 이득이 증가합니다. 이 경우 피드백 경로의 이득이 음수이므로 'GH'값은 음수입니다.

• (1 + GH) 값이 1보다 크면 전체 이득이 감소합니다. 이 경우 'GH'값은 피드백 경로의 이득이 양이므로 양수입니다.

일반적으로 'G'와 'H'는 주파수의 함수입니다. 따라서 피드백은 한 주파수 범위에서 시스템의 전체 이득을 증가시키고 다른 주파수 범위에서 감소합니다.

감도에 대한 피드백의 영향

Sensitivity 네거티브 피드백 폐쇄 루프 제어 시스템의 전체 이득 (T) 개방 루프 게인 (G)는 다음과 같이 정의됩니다.

$S_{G}^{T} = \frac{\frac{\partial T}{T}}{\frac{\partial G}{G}}=\frac{Percentage\: change \: in \:T}{Percentage\: change \: in \:G}$ (수식 3)

어디, ∂T G의 증분 변경으로 인한 T의 증분 변경입니다.

방정식 3을 다음과 같이 다시 작성할 수 있습니다.

$S_{G}^{T}=\frac{\partial T}{\partial G}\frac{G}{T}$ (수식 4)

방정식 2의 양쪽에서 G에 대해 편미분을 수행합니다.

$\frac{\partial T}{\partial G}=\frac{\partial}{\partial G}\left (\frac{G}{1+GH} \right )=\frac{(1+GH).1-G(H)}{(1+GH)^2}=\frac{1}{(1+GH)^2}$ (수식 5)

방정식 2에서 다음을 얻을 수 있습니다.

$\frac{G}{T}=1+GH$ (수식 6)

방정식 4에서 방정식 5와 방정식 6을 대입합니다.

$$S_{G}^{T}=\frac{1}{(1+GH)^2}(1+GH)=\frac{1}{1+GH}$$

그래서 우리는 sensitivity(1 + GH)의 역수로 폐쇄 루프 제어 시스템의 전체 이득의. 따라서 감도는 (1 + GH) 값에 따라 증가하거나 감소 할 수 있습니다.

• (1 + GH) 값이 1보다 작 으면 감도가 증가합니다. 이 경우 피드백 경로의 이득이 음수이므로 'GH'값은 음수입니다.

• (1 + GH) 값이 1보다 크면 감도가 감소합니다. 이 경우 'GH'값은 피드백 경로의 이득이 양이므로 양수입니다.

일반적으로 'G'와 'H'는 주파수의 함수입니다. 따라서 피드백은 한 주파수 범위에서 시스템 이득의 감도를 증가시키고 다른 주파수 범위에서 감소합니다. 따라서 시스템이 매개 변수 변동에 덜 민감하거나 덜 민감하도록 'GH'값을 선택해야합니다.

피드백이 안정성에 미치는 영향

• 출력이 제어되는 경우 시스템은 안정적이라고합니다. 그렇지 않으면 불안정하다고합니다.

• 방정식 2에서 분모 값이 0이면 (예 : GH = -1) 제어 시스템의 출력은 무한합니다. 따라서 제어 시스템이 불안정 해집니다.

따라서 제어 시스템을 안정적으로 만들기 위해서는 피드백을 적절히 선택해야합니다.

피드백이 소음에 미치는 영향

피드백이 노이즈에 미치는 영향을 알기 위해 노이즈 신호만으로 인한 피드백이있는 경우와없는 경우의 전달 함수 관계를 비교해 보겠습니다.

고려 open loop control system 아래와 같이 노이즈 신호가 있습니다.

그만큼 open loop transfer function 노이즈 신호만으로도

$\frac{C(s)}{N(s)}=G_b$ (수식 7)

다른 입력을하여 얻습니다. $R(s)$ 0과 같습니다.

고려 closed loop control system 아래와 같이 노이즈 신호가 있습니다.

그만큼 closed loop transfer function 노이즈 신호만으로도

$\frac{C(s)}{N(s)}=\frac{G_b}{1+G_aG_bH}$ (수식 8)

다른 입력을하여 얻습니다. $R(s)$ 0과 같습니다.

방정식 7과 방정식 8을 비교하고,

폐쇄 루프 제어 시스템에서 노이즈 신호로 인한 이득은 $(1+G_a G_b H)$ 그 용어가 $(1+G_a G_b H)$ 1보다 큽니다.

제어 시스템은 다음과 같은 수학 방정식 세트로 표현할 수 있습니다. mathematical model. 이 모델은 제어 시스템의 분석 및 설계에 유용합니다. 제어 시스템의 분석은 입력 및 수학적 모델을 알 때 출력을 찾는 것을 의미합니다. 제어 시스템의 설계는 입력과 출력을 알 때 수학적 모델을 찾는 것을 의미합니다.

다음과 같은 수학적 모델이 주로 사용됩니다.

• 미분 방정식 모델
• 전달 함수 모델
• 상태 공간 모델

이 장에서 처음 두 가지 모델에 대해 설명하겠습니다.

미분 방정식 모델

미분 방정식 모델은 제어 시스템의 시간 도메인 수학적 모델입니다. 미분 방정식 모델의 경우 다음 단계를 따르십시오.

• 주어진 제어 시스템에 기본 법칙을 적용하십시오.

• 중간 변수를 제거하여 입력 및 출력 측면에서 미분 방정식을 얻습니다.

예

다음 그림에 표시된대로 다음 전기 시스템을 고려하십시오. 이 회로는 저항, 인덕터 및 커패시터로 구성됩니다. 이 모든 전기 요소는series. 이 회로에 적용되는 입력 전압은$v_i$ 커패시터 양단의 전압은 출력 전압입니다. $v_o$.

이 회로에 대한 메시 방정식은 다음과 같습니다.

$$v_i=Ri+L\frac{\text{d}i}{\text{d}t}+v_o$$

대체, 커패시터를 통과하는 전류 $i=c\frac{\text{d}v_o}{\text{d}t}$ 위의 방정식에서.

$$\Rightarrow\:v_i=RC\frac{\text{d}v_o}{\text{d}t}+LC\frac{\text{d}^2v_o}{\text{d}t^2}+v_o$$

$$\Rightarrow\frac{\text{d}^2v_o}{\text{d}t^2}+\left ( \frac{R}{L} \right )\frac{\text{d}v_o}{\text{d}t}+\left ( \frac{1}{LC} \right )v_o=\left ( \frac{1}{LC} \right )v_i$$

위의 방정식은 2 차입니다 differential equation.

전달 함수 모델

전달 함수 모델은 제어 시스템의 s 영역 수학적 모델입니다. 그만큼Transfer function LTI (Linear Time Invariant) 시스템의 경우 모든 초기 조건이 0이라고 가정하여 출력의 라플라스 변환과 입력의 라플라스 변환의 비율로 정의됩니다.

만약 $x(t)$ 과 $y(t)$ LTI 시스템의 입력 및 출력 인 경우 해당 라플라스 변환은 다음과 같습니다. $X(s)$ 과 $Y(s)$.

따라서 LTI 시스템의 전달 함수는 다음의 비율과 같습니다. $Y(s)$ 과 $X(s)$.

$$i.e.,\: Transfer\: Function =\frac{Y(s)}{X(s)}$$

LTI 시스템의 전달 함수 모델은 다음 그림에 나와 있습니다.

여기서 우리는 내부에 전달 함수가있는 블록이있는 LTI 시스템을 나타냅니다. 이 블록에는 입력이 있습니다.$X(s)$ & 출력 $Y(s)$.

예

이전에 우리는 전기 시스템의 미분 방정식을 다음과 같이 얻었습니다.

$$\frac{\text{d}^2v_o}{\text{d}t^2}+\left ( \frac{R}{L} \right )\frac{\text{d}v_o}{\text{d}t}+\left ( \frac{1}{LC} \right )v_o=\left ( \frac{1}{LC} \right )v_i$$

양쪽에 라플라스 변환을 적용합니다.

$$s^2V_o(s)+\left ( \frac{sR}{L} \right )V_o(s)+\left ( \frac{1}{LC} \right )V_o(s)=\left ( \frac{1}{LC} \right )V_i(s)$$

$$\Rightarrow \left \{ s^2+\left ( \frac{R}{L} \right )s+\frac{1}{LC} \right \}V_o(s)=\left ( \frac{1}{LC} \right )V_i(s)$$

$$\Rightarrow \frac{V_o(s)}{V_i(s)}=\frac{\frac{1}{LC}}{s^2+\left ( \frac{R}{L} \right )s+\frac{1}{LC}}$$

어디,

• $v_i(s)$ 입력 전압의 라플라스 변환 $v_i$

• $v_o(s)$ 출력 전압의 라플라스 변환 $v_o$

위의 방정식은 transfer function2 차 전기 시스템의. 이 시스템의 전달 함수 모델은 다음과 같습니다.

여기에서는 내부에 전달 함수가있는 블록이있는 2 차 전기 시스템을 보여줍니다. 이 블록에는 입력이 있습니다.$V_i(s)$ & 출력 $V_o(s)$.

이 장에서는 differential equation modeling기계 시스템의. 동작 유형에 따라 두 가지 유형의 기계 시스템이 있습니다.

• 중개 기계 시스템
• 회전 기계 시스템

중개 기계 시스템 모델링

중개 기계 시스템은 straight line. 이러한 시스템은 주로 세 가지 기본 요소로 구성됩니다. 그것들은 질량, 스프링 및 대시 팟 또는 댐퍼입니다.

병진 기계 시스템에 힘이 가해지면 시스템의 질량, 탄성 및 마찰로 인해 반대되는 힘에 의해 반대됩니다. 적용된 힘과 반대되는 힘이 반대 방향에 있기 때문에 시스템에 작용하는 힘의 대수적 합은 0입니다. 이제이 세 가지 요소가 반대하는 힘을 개별적으로 살펴 보겠습니다.

질량

질량은 신체의 속성입니다. kinetic energy. 질량이있는 몸체에 힘이 가해지면M, 질량 때문에 반대되는 힘에 의해 반대됩니다. 이 반대 힘은 신체의 가속도에 비례합니다. 탄성과 마찰은 무시할 만하다고 가정합니다.

$$F_m\propto\: a$$

$$\Rightarrow F_m=Ma=M\frac{\text{d}^2x}{\text{d}t^2}$$

$$F=F_m=M\frac{\text{d}^2x}{\text{d}t^2}$$

어디,

• F 적용된 힘

• F_m 질량으로 인한 반대 힘

• M 질량이다

• a 가속이다

• x 변위

봄

봄은 저장하는 요소입니다. potential energy. 스프링에 힘이 가해지면K, 그러면 스프링의 탄성으로 인해 반대되는 힘에 의해 반대됩니다. 이 반대 힘은 스프링의 변위에 비례합니다. 질량과 마찰은 무시할 만하다고 가정합니다.

$$F\propto\: x$$

$$\Rightarrow F_k=Kx$$

$$F=F_k=Kx$$

어디,

• F 적용된 힘

• F_k 스프링의 탄성으로 인한 반대 힘

• K 봄 상수

• x 변위

Dashpot

대시 포트에 힘이 가해지면 B, 다음으로 인해 반대 세력에 의해 반대 friction대시 팟의. 이 반대 힘은 신체의 속도에 비례합니다. 질량과 탄성이 무시할 만하다고 가정합니다.

$$F_b\propto\: \nu$$

$$\Rightarrow F_b=B\nu=B\frac{\text{d}x}{\text{d}t}$$

$$F=F_b=B\frac{\text{d}x}{\text{d}t}$$

어디,

• F_b 대시 포트의 마찰로 인한 반대 힘

• B 마찰 계수입니다

• v 속도

• x 변위

회전 기계 시스템의 모델링

회전 기계 시스템은 고정 된 축을 중심으로 이동합니다. 이러한 시스템은 주로 세 가지 기본 요소로 구성됩니다. 사람들은moment of inertia, torsional spring 과 dashpot.

회전 기계 시스템에 토크가 적용되면 시스템의 관성 모멘트, 탄성 및 마찰로 인한 반대 토크에 의해 반대됩니다. 적용된 토크와 반대 토크가 반대 방향에 있기 때문에 시스템에 작용하는 토크의 대수 합계는 0입니다. 이제이 세 요소가 반대하는 토크를 개별적으로 살펴 보겠습니다.

관성 모멘트

병진 기계 시스템에서 질량은 운동 에너지를 저장합니다. 마찬가지로, 회전 기계 시스템에서 관성 모멘트는kinetic energy.

관성 모멘트가있는 몸체에 토크를 가하면 J, 관성 모멘트로 인해 반대 토크에 의해 반대됩니다. 이 반대 토크는 신체의 각가속도에 비례합니다. 탄성과 마찰은 무시할 만하다고 가정합니다.

$$T_j\propto\: \alpha$$

$$\Rightarrow T_j=J\alpha=J\frac{\text{d}^2\theta}{\text{d}t^2}$$

$$T=T_j=J\frac{\text{d}^2\theta}{\text{d}t^2}$$

어디,

• T 적용된 토크

• T_j 관성 모멘트로 인한 반대 토크

• J 관성 모멘트

• α 각가속도

• θ 각도 변위

비틀림 스프링

병진 기계 시스템에서 스프링은 위치 에너지를 저장합니다. 마찬가지로 회전 기계 시스템에서 비틀림 스프링 저장potential energy.

비틀림 스프링에 토크가 적용되는 경우 K, 그러면 비틀림 스프링의 탄성으로 인해 반대 토크가 반대됩니다. 이 반대 토크는 비틀림 스프링의 각도 변위에 비례합니다. 관성 모멘트와 마찰은 무시할 만하다고 가정합니다.

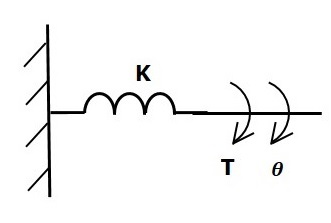
$$T_k\propto\: \theta$$

$$\Rightarrow T_k=K\theta$$

$$T=T_k=K\theta$$

어디,

• T 적용된 토크

• T_k 비틀림 스프링의 탄성으로 인한 반대 토크

• K 비틀림 스프링 상수

• θ 각도 변위

Dashpot

대시 포트에 토크가 적용되는 경우 B, 다음으로 인해 반대 토크에 의해 반대 rotational friction대시 팟의. 이 반대 토크는 신체의 각속도에 비례합니다. 관성 모멘트와 탄성이 무시할 만하다고 가정합니다.

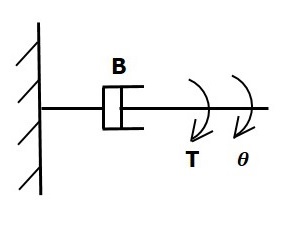
$$T_b\propto\: \omega$$

$$\Rightarrow T_b=B\omega=B\frac{\text{d}\theta}{\text{d}t}$$

$$T=T_b=B\frac{\text{d}\theta}{\text{d}t}$$

어디,

• T_b 대시 포트의 회전 마찰로 인한 반대 토크

• B 회전 마찰 계수

• ω 각속도

• θ 각 변위입니다

두 시스템은 analogous 다음 두 가지 조건이 충족되면 서로에게.

• 두 시스템은 물리적으로 다릅니다.
• 이 두 시스템의 미분 방정식 모델링은 동일합니다.

전기 시스템과 기계 시스템은 물리적으로 다른 두 시스템입니다. 병진 기계 시스템의 전기적 비유에는 두 가지 유형이 있습니다. 그것들은 힘 전압 비유와 힘 전류 비유입니다.

힘 전압 유추

힘 전압 비유에서 수학 방정식 translational mechanical system 전기 시스템의 메쉬 방정식과 비교됩니다.

다음 그림에 표시된대로 다음 변환 기계 시스템을 고려하십시오.

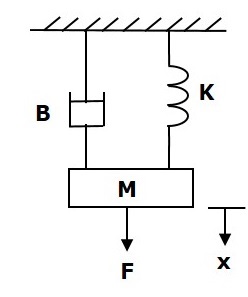
그만큼 force balanced equation 이 시스템은

$$F=F_m+F_b+F_k$$

$\Rightarrow F=M\frac{\text{d}^2x}{\text{d}t^2}+B\frac{\text{d}x}{\text{d}t}+Kx$ (Equation 1)

다음 그림에 표시된대로 다음 전기 시스템을 고려하십시오. 이 회로는 저항, 인덕터 및 커패시터로 구성됩니다. 이 모든 전기 요소는 직렬로 연결됩니다. 이 회로에 적용되는 입력 전압은$V$ 볼트와 회로를 통해 흐르는 전류는 $i$ 암페어.

이 회로에 대한 메시 방정식은 다음과 같습니다.

$V=Ri+L\frac{\text{d}i}{\text{d}t}+\frac{1}{c}\int idt$ (Equation 2)

대용품, $i=\frac{\text{d}q}{\text{d}t}$ 방정식 2에서.

$$V=R\frac{\text{d}q}{\text{d}t}+L\frac{\text{d}^2q}{\text{d}t^2}+\frac{q}{C}$$

$\Rightarrow V=L\frac{\text{d}^2q}{\text{d}t^2}+R\frac{\text{d}q}{\text{d}t}+\left ( \frac{1}{c} \right )q$ (Equation 3)

방정식 1과 방정식 3을 비교하면 병진 기계 시스템과 전기 시스템의 유사한 양을 얻을 수 있습니다. 다음 표는 이러한 유사한 수량을 보여줍니다.

중개 기계 시스템	전기 시스템
힘 (F)	전압 (V)
질량 (M)	인덕턴스 (L)
마찰 계수 (B)	저항 (R)
스프링 상수 (K)	커패시턴스의 역수 $(\frac{1}{c})$
변위 (x)	요금 (q)
속도 (v)	전류 (i)

마찬가지로 회전 기계 시스템에 대한 토크 전압 비유가 있습니다. 이제이 비유에 대해 논의하겠습니다.

토크 전압 유추

이 비유에서 수학 방정식 rotational mechanical system 전기 시스템의 메쉬 방정식과 비교됩니다.

회전 기계 시스템은 다음 그림에 나와 있습니다.

토크 균형 방정식은 다음과 같습니다.

$$T=T_j+T_b+T_k$$

$\Rightarrow T=J\frac{\text{d}^2\theta}{\text{d}t^2}+B\frac{\text{d}\theta}{\text{d}t}+k\theta$ (Equation 4)

방정식 4와 방정식 3을 비교하면 회전 기계 시스템과 전기 시스템의 유사한 양을 얻을 수 있습니다. 다음 표는 이러한 유사한 수량을 보여줍니다.

회전 기계 시스템	전기 시스템
토크 (T)	전압 (V)
관성 모멘트 (J)	인덕턴스 (L)
회전 마찰 계수 (B)	저항 (R)
비틀림 스프링 상수 (K)	커패시턴스의 역수 $(\frac{1}{c})$
각도 변위 (θ)	요금 (q)
각속도 (ω)	전류 (i)

강제 전류 유추

현재의 비유에서, 수학 방정식은 translational mechanical system 전기 시스템의 절점 방정식과 비교됩니다.

다음 그림에 표시된대로 다음 전기 시스템을 고려하십시오. 이 회로는 전류원, 저항기, 인덕터 및 커패시터로 구성됩니다. 이 모든 전기 요소는 병렬로 연결됩니다.

절점 방정식은 다음과 같습니다.

$i=\frac{V}{R}+\frac{1}{L}\int Vdt+C\frac{\text{d}V}{\text{d}t}$ (Equation 5)

대용품, $V=\frac{\text{d}\Psi}{\text{d}t}$ 방정식 5에서.

$$i=\frac{1}{R}\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi+C\frac{\text{d}^2\Psi}{\text{d}t^2}$$

$\Rightarrow i=C\frac{\text{d}^2\Psi}{\text{d}t^2}+\left ( \frac{1}{R} \right )\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi$ (Equation 6)

방정식 1과 방정식 6을 비교하면 병진 기계 시스템과 전기 시스템의 유사한 양을 얻을 수 있습니다. 다음 표는 이러한 유사한 수량을 보여줍니다.

중개 기계 시스템	전기 시스템
힘 (F)	전류 (i)
질량 (M)	커패시턴스 (C)
마찰 계수 (B)	저항의 역수$(\frac{1}{R})$
스프링 상수 (K)	인덕턴스의 역수$(\frac{1}{L})$
변위 (x)	자속 (ψ)
속도 (v)	전압 (V)

마찬가지로 회전 기계 시스템에 대한 토크 전류 비유가 있습니다. 이제이 비유를 논의하겠습니다.

토크 전류 비유

이 비유에서 수학 방정식은 rotational mechanical system 전기 시스템의 노드 메시 방정식과 비교됩니다.

방정식 4와 방정식 6을 비교하면 회전 기계 시스템과 전기 시스템의 유사한 양을 얻을 수 있습니다. 다음 표는 이러한 유사한 수량을 보여줍니다.

회전 기계 시스템	전기 시스템
토크 (T)	전류 (i)
관성 모멘트 (J)	커패시턴스 (C)
회전 마찰 계수 (B)	저항의 역수$(\frac{1}{R})$
비틀림 스프링 상수 (K)	인덕턴스의 역수$(\frac{1}{L})$
각도 변위 (θ)	자속 (ψ)
각속도 (ω)	전압 (V)

이 장에서는 기계 시스템의 전기적 유사성에 대해 논의했습니다. 이러한 비유는 유사한 전기 시스템의 기계 시스템과 같은 비 전기 시스템을 연구하고 분석하는 데 도움이됩니다.

블록 다이어그램은 단일 블록 또는 블록 조합으로 구성됩니다. 이들은 제어 시스템을 그림 형식으로 표현하는 데 사용됩니다.

블록 다이어그램의 기본 요소

블록 다이어그램의 기본 요소는 블록, 합산 지점 및 이륙 지점입니다. 이러한 요소를 식별하기 위해 다음 그림에 표시된 폐 루프 제어 시스템의 블록 다이어그램을 고려해 보겠습니다.

위의 블록 다이어그램은 전달 함수 G (s)와 H (s)가있는 두 개의 블록으로 구성됩니다. 또한 하나의 합산 지점과 하나의 이륙 지점이 있습니다. 화살표는 신호 흐름의 방향을 나타냅니다. 이제 이러한 요소를 하나씩 논의하겠습니다.

블록

구성 요소의 전달 함수는 블록으로 표시됩니다. 블록에는 단일 입력 및 단일 출력이 있습니다.

다음 그림은 입력 X (s), 출력 Y (s) 및 전달 함수 G (s)가있는 블록을 보여줍니다.

전달 함수,$G(s)=\frac{Y(s)}{X(s)}$

$$\Rightarrow Y(s)=G(s)X(s)$$

블록의 출력은 입력과 블록의 전달 함수를 곱하여 얻습니다.

합산 점

합산 점은 내부에 십자 (X)가있는 원으로 표시됩니다. 두 개 이상의 입력과 단일 출력이 있습니다. 입력의 대수 합계를 생성합니다. 또한 입력의 극성을 기반으로 입력의 합산 또는 빼기 또는 합산 및 빼기 조합을 수행합니다. 이 세 가지 작업을 하나씩 살펴 보겠습니다.

다음 그림은 두 개의 입력 (A, B)과 하나의 출력 (Y)이있는 합산 지점을 보여줍니다. 여기에서 입력 A와 B는 양의 부호를 갖습니다. 따라서 합산 점은 출력 Y를 다음과 같이 생성합니다.sum of A and B.

즉, Y = A + B.

다음 그림은 두 개의 입력 (A, B)과 하나의 출력 (Y)이있는 합산 지점을 보여줍니다. 여기에서 입력 A와 B는 반대 부호를 가지고 있습니다. 즉, A는 양수 부호이고 B는 음수 부호입니다. 따라서 합산 점은 출력을 생성합니다.Y 로 difference of A and B.

Y = A + (-B) = A-B.

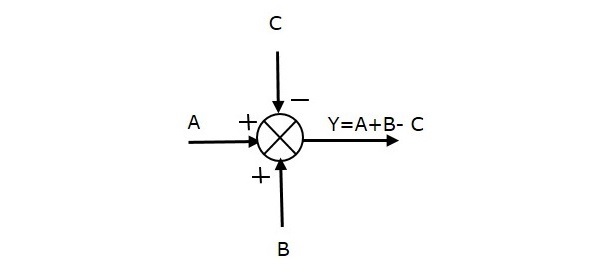
다음 그림은 3 개의 입력 (A, B, C)과 1 개의 출력 (Y)이있는 합산 지점을 보여줍니다. 여기에서 입력 A와 B는 양수 부호이고 C는 음수 부호입니다. 따라서 합산 점은 출력을 생성합니다.Y 같이

Y = A + B + (−C) = A + B − C.

이륙 지점

이륙 지점은 동일한 입력 신호가 둘 이상의 분기를 통과 할 수있는 지점입니다. 즉, 이륙 지점의 도움으로 동일한 입력을 하나 이상의 블록, 합산 지점에 적용 할 수 있습니다.

다음 그림에서 이륙 지점은 동일한 입력 R (s)를 두 개의 추가 블록에 연결하는 데 사용됩니다.

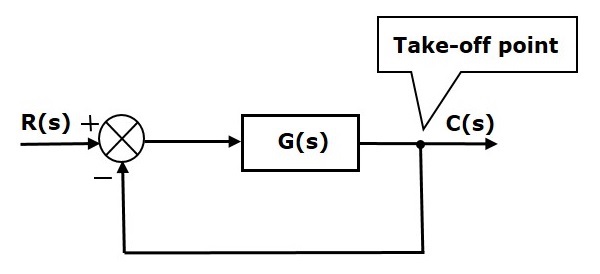
다음 그림에서 이륙 지점은 합산 지점에 대한 입력 중 하나로 출력 C (s)를 연결하는 데 사용됩니다.

전기 시스템의 블록 다이어그램 표현

이 섹션에서는 블록 다이어그램으로 전기 시스템을 표현해 보겠습니다. 전기 시스템은 주로 세 가지 기본 요소를 포함합니다.resistor, inductor and capacitor.

다음 그림과 같이 일련의 RLC 회로를 고려하십시오. 여기서 V _i (t) 및 V _o (t)는 입력 및 출력 전압입니다. i (t)를 회로를 통과하는 전류라고합시다. 이 회로는 시간 영역에 있습니다.

이 회로에 Laplace 변환을 적용하면 s 도메인의 회로를 얻을 수 있습니다. 회로는 다음 그림과 같습니다.

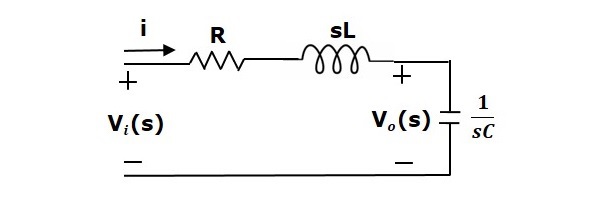
위의 회로에서 다음과 같이 쓸 수 있습니다.

$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$

$\Rightarrow I(s)=\left \{ \frac{1}{R+sL} \right \}\left \{ V_i(s)-V_o(s) \right \}$ (Equation 1)

$V_o(s)=\left ( \frac{1}{sC} \right )I(s)$ (Equation 2)

이제이 두 방정식에 대한 블록 다이어그램을 개별적으로 그려 보겠습니다. 그런 다음 일련의 RLC 회로 (s- 도메인)의 전체 블록 다이어그램을 얻기 위해 이러한 블록 다이어그램을 적절하게 결합합니다.

수학 식 1은 전달 함수를 갖는 블록으로 구현 될 수 있으며, $\frac{1}{R+sL}$. 이 블록의 입력 및 출력은 다음과 같습니다.$\left \{ V_i(s)-V_o(s) \right \}$ 과 $I(s)$. 우리는 얻기 위해 합산 점이 필요합니다.$\left \{ V_i(s)-V_o(s) \right \}$. 방정식 1의 블록 다이어그램은 다음 그림에 나와 있습니다.

수학 식 2는 전달 함수가있는 블록으로 구현 될 수 있습니다. $\frac{1}{sC}$. 이 블록의 입력 및 출력은 다음과 같습니다.$I(s)$ 과 $V_o(s)$. 방정식 2의 블록 다이어그램은 다음 그림에 나와 있습니다.

일련의 RLC 회로 (s- 도메인)의 전체 블록 다이어그램이 다음 그림에 나와 있습니다.

마찬가지로, 당신은 block diagram 이 간단한 절차에 따라 모든 전기 회로 또는 시스템의.

• Laplace 변환을 적용하여 시간 도메인 전기 회로를 s 도메인 전기 회로로 변환합니다.

• 모든 분로 분기에서 모든 직렬 분기 요소와 전압을 통과하는 전류에 대한 방정식을 기록합니다.

• 위의 모든 방정식에 대한 블록 다이어그램을 개별적으로 그립니다.

• 전기 회로 (s- 도메인)의 전체 블록 다이어그램을 얻기 위해이 모든 블록 다이어그램을 적절하게 결합하십시오.

블록 다이어그램 대수는 블록 다이어그램의 기본 요소와 관련된 대수 일뿐입니다. 이 대수는 대수 방정식의 그림 표현을 다룹니다.

블록에 대한 기본 연결

두 블록 사이에는 세 가지 기본 연결 유형이 있습니다.

시리즈 연결

직렬 연결이라고도합니다. cascade connection. 다음 그림에서 전달 함수가있는 두 블록$G_1(s)$ 과 $G_2(s)$ 직렬로 연결됩니다.

이 조합의 경우 출력을 얻습니다. $Y(s)$ 같이

$$Y(s)=G_2(s)Z(s)$$

어디, $Z(s)=G_1(s)X(s)$

$$\Rightarrow Y(s)=G_2(s)[G_1(s)X(s)]=G_1(s)G_2(s)X(s)$$

$$\Rightarrow Y(s)=\lbrace G_1(s)G_2(s)\rbrace X(s)$$

이 방정식을 출력 방정식의 표준 형식과 비교하십시오. $Y(s)=G(s)X(s)$. 어디,$G(s) = G_1(s)G_2(s)$.

이는 우리가 series connection단일 블록으로 두 블록의. 이 단일 블록의 전달 함수는product of the transfer functions그 두 블록의. 동등한 블록 다이어그램이 아래에 나와 있습니다.

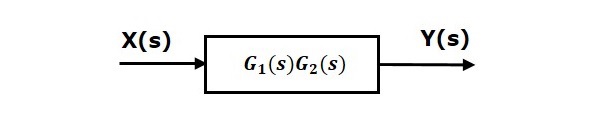
마찬가지로 단일 블록으로 'n'블록의 직렬 연결을 나타낼 수 있습니다. 이 단일 블록의 전달 함수는 모든 'n'블록의 전달 함수의 곱입니다.

병렬 연결

연결되는 블록 parallel 가질 것이다 same input. 다음 그림에서 전달 함수가있는 두 블록$G_1(s)$ 과 $G_2(s)$병렬로 연결됩니다. 이 두 블록의 출력은 합산 지점에 연결됩니다.

이 조합의 경우 출력을 얻습니다. $Y(s)$ 같이

$$Y(s)=Y_1(s)+Y_2(s)$$

어디, $Y_1(s)=G_1(s)X(s)$ 과 $Y_2(s)=G_2(s)X(s)$

$$\Rightarrow Y(s)=G_1(s)X(s)+G_2(s)X(s)=\lbrace G_1(s)+G_2(s)\rbrace X(s)$$

이 방정식을 출력 방정식의 표준 형식과 비교하십시오. $Y(s)=G(s)X(s)$.

어디, $G(s)=G_1(s)+G_2(s)$.

이는 우리가 parallel connection단일 블록으로 두 블록의. 이 단일 블록의 전달 함수는sum of the transfer functions그 두 블록의. 동등한 블록 다이어그램이 아래에 나와 있습니다.

마찬가지로 단일 블록으로 'n'블록의 병렬 연결을 나타낼 수 있습니다. 이 단일 블록의 전달 함수는 모든 'n'블록의 전달 함수의 대수적 합입니다.

피드백 연결

이전 장에서 논의했듯이 두 가지 유형의 feedback— 긍정적 인 피드백과 부정적인 피드백. 다음 그림은 네거티브 피드백 제어 시스템을 보여줍니다. 여기서 전달 기능을 가진 두 블록$G(s)$ 과 $H(s)$ 닫힌 루프를 형성합니다.

합산 점의 출력은 다음과 같습니다.

$$E(s)=X(s)-H(s)Y(s)$$

출력 $Y(s)$ -

$$Y(s)=E(s)G(s)$$

대용품 $E(s)$ 위 방정식의 값.

$$Y(s)=\left \{ X(s)-H(s)Y(s)\rbrace G(s) \right\}$$

$$Y(s)\left \{ 1+G(s)H(s)\rbrace = X(s)G(s) \right\}$$

$$\Rightarrow \frac{Y(s)}{X(s)}=\frac{G(s)}{1+G(s)H(s)}$$

따라서 네거티브 피드백 폐쇄 루프 전달 함수는 다음과 같습니다. $\frac{G(s)}{1+G(s)H(s)}$

이는 단일 블록으로 두 블록의 부정적인 피드백 연결을 나타낼 수 있음을 의미합니다. 이 단일 블록의 전달 함수는 네거티브 피드백의 폐쇄 루프 전달 함수입니다. 동등한 블록 다이어그램이 아래에 나와 있습니다.

마찬가지로 단일 블록으로 두 블록의 긍정적 인 피드백 연결을 나타낼 수 있습니다. 이 단일 블록의 전달 함수는 포지티브 피드백의 폐 루프 전달 함수입니다.$\frac{G(s)}{1-G(s)H(s)}$

포인트 합산을위한 블록 다이어그램 대수

블록과 관련하여 합산 점을 이동하는 두 가지 가능성이 있습니다.

• 블록 후 합산 지점 이동
• 블록 앞의 합산 지점 이동

이제 위의 두 가지 경우에 하나씩 어떤 종류의 준비를해야하는지 살펴 보겠습니다.

블록 후 합산 지점 이동

다음 그림에 표시된 블록 다이어그램을 고려하십시오. 여기에서 합산 ​​지점은 블록 앞에 있습니다.

합산 점에는 두 개의 입력이 있습니다. $R(s)$ 과 $X(s)$. 그것의 출력은$\left \{R(s)+X(s)\right\}$.

따라서 블록에 대한 입력 $G(s)$ 이다 $\left \{R(s)+X(s)\right \}$ 그 결과는 –

$$Y(s)=G(s)\left \{R(s)+X(s)\right \}$$

$\Rightarrow Y(s)=G(s)R(s)+G(s)X(s)$ (Equation 1)

이제 블록 뒤의 합산 지점을 이동하십시오. 이 블록 다이어그램은 다음 그림에 나와 있습니다.

블록의 출력 $G(s)$ 이다 $G(s)R(s)$.

합산 점의 출력은 다음과 같습니다.

$Y(s)=G(s)R(s)+X(s)$ (Equation 2)

방정식 1과 방정식 2를 비교합니다.

첫 학기 $‘G(s) R(s)’$두 방정식에서 동일합니다. 그러나 두 번째 학기에 차이가 있습니다. 두 번째 항도 동일하게하려면 블록이 하나 더 필요합니다.$G(s)$. 입력이 있습니다.$X(s)$ 이 블록의 출력은 대신 합산 점에 대한 입력으로 제공됩니다. $X(s)$. 이 블록 다이어그램은 다음 그림에 나와 있습니다.

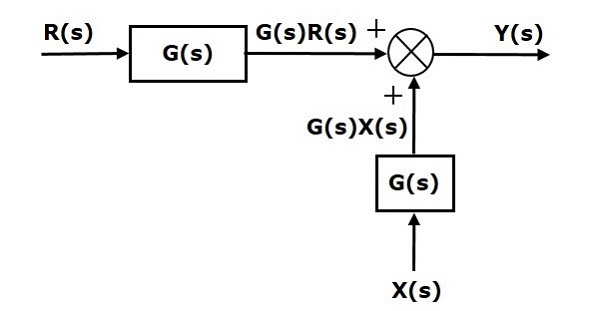
블록 앞의 합산 지점 이동

다음 그림에 표시된 블록 다이어그램을 고려하십시오. 여기에서 합산 ​​지점은 블록 뒤에 있습니다.

이 블록 다이어그램의 출력은 다음과 같습니다.

$Y(s)=G(s)R(s)+X(s)$ (Equation 3)

이제 합산 지점을 블록 앞으로 이동하십시오. 이 블록 다이어그램은 다음 그림에 나와 있습니다.

이 블록 다이어그램의 출력은 다음과 같습니다.

$Y(S)=G(s)R(s)+G(s)X(s)$ (Equation 4)

방정식 3과 방정식 4를 비교하고,

첫 학기 $‘G(s) R(s)’$두 방정식에서 동일합니다. 그러나 두 번째 학기에 차이가 있습니다. 두 번째 항도 동일하게하려면 블록이 하나 더 필요합니다.$\frac{1}{G(s)}$. 입력이 있습니다.$X(s)$ 이 블록의 출력은 대신 합산 점에 대한 입력으로 제공됩니다. $X(s)$. 이 블록 다이어그램은 다음 그림에 나와 있습니다.

이륙 지점에 대한 블록 다이어그램 대수

블록과 관련하여 이륙 지점을 이동할 수있는 두 가지 가능성이 있습니다.

• 블록 후 이륙 지점 이동
• 블록 전 이륙 지점 이동

이제 위의 두 가지 경우에 하나씩, 어떤 종류의 준비가 이루어져야하는지 살펴 보겠습니다.

블록 후 이륙 지점 이동

다음 그림에 표시된 블록 다이어그램을 고려하십시오. 이 경우 이륙 지점은 블록 앞에 있습니다.

여기, $X(s)=R(s)$ 과 $Y(s)=G(s)R(s)$

블록 이후 이륙 지점을 이동하면 출력이 $Y(s)$동일합니다. 그러나 차이가 있습니다.$X(s)$값. 그래서, 같은 것을 얻으려면$X(s)$ 값, 우리는 하나 더 블록이 필요합니다 $\frac{1}{G(s)}$. 입력이 있습니다.$Y(s)$ 출력은 $X(s)$. 이 블록 다이어그램은 다음 그림에 나와 있습니다.

블록 전 이륙 지점 이동

다음 그림에 표시된 블록 다이어그램을 고려하십시오. 여기에서 이륙 지점은 블록 뒤에 있습니다.

여기, $X(s)=Y(s)=G(s)R(s)$

블록 앞의 이륙 지점을 이동하면 출력이 $Y(s)$동일합니다. 그러나 차이가 있습니다.$X(s)$값. 그래서, 같은 것을 얻기 위해$X(s)$ 값, 우리는 하나 더 블록이 필요합니다 $G(s)$. 입력이 있습니다.$R(s)$ 출력은 $X(s)$. 이 블록 다이어그램은 다음 그림에 나와 있습니다.

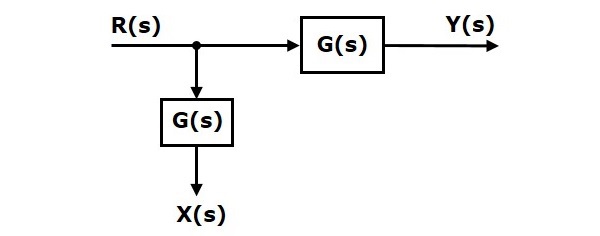
이전 장에서 논의 된 개념은 블록 다이어그램을 축소 (단순화)하는 데 도움이됩니다.

블록 다이어그램 축소 규칙

많은 블록, 합산 지점 및 이륙 지점이있는 블록 다이어그램을 단순화 (축소)하려면 다음 규칙을 따르십시오.

• Rule 1 − 직렬로 연결된 블록을 확인하고 단순화합니다.

• Rule 2 − 병렬로 연결된 블록을 확인하고 단순화합니다.

• Rule 3 − 피드백 루프에 연결된 블록을 확인하고 단순화합니다.

• Rule 4 − 단순화하면서 이륙 지점에 어려움이 있으면 오른쪽으로 이동합니다.

• Rule 5 − 단순화시 합산에 어려움이있는 경우 왼쪽으로 이동합니다.

• Rule 6 − 단순화 된 형태, 즉 단일 블록을 얻을 때까지 위의 단계를 반복합니다.

Note −이 단일 블록에있는 전달 함수는 전체 블록 다이어그램의 전달 함수입니다.

예

다음 그림에 표시된 블록 다이어그램을 고려하십시오. 블록 다이어그램 축소 규칙을 사용하여이 블록 다이어그램을 단순화 (축소)합시다.

Step 1 − 블록에 규칙 1 사용 $G_1$ 과 $G_2$. 블록에 규칙 2 사용$G_3$ 과 $G_4$. 수정 된 블록 다이어그램은 다음 그림과 같습니다.

Step 2 − 블록에 규칙 3 사용 $G_1G_2$ 과 $H_1$. 블록 이후 이륙 지점을 이동하려면 규칙 4를 사용하십시오.$G_5$. 수정 된 블록 다이어그램은 다음 그림과 같습니다.

Step 3 − 블록에 규칙 1 사용 $(G_3 + G_4)$ 과 $G_5$. 수정 된 블록 다이어그램은 다음 그림과 같습니다.

Step 4 − 블록에 규칙 3 사용 $(G_3 + G_4)G_5$ 과 $H_3$. 수정 된 블록 다이어그램은 다음 그림과 같습니다.

Step 5− 직렬로 연결된 블록에는 규칙 1을 사용하십시오. 수정 된 블록 다이어그램은 다음 그림과 같습니다.

Step 6− 피드백 루프에 연결된 블록에는 규칙 3을 사용하십시오. 수정 된 블록 다이어그램은 다음 그림과 같습니다. 이것은 단순화 된 블록 다이어그램입니다.

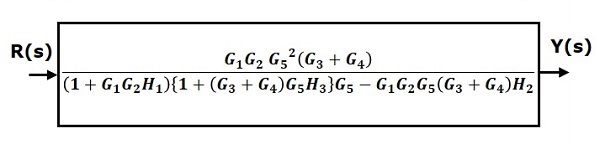
따라서 시스템의 전달 함수는

$$\frac{Y(s)}{R(s)}=\frac{G_1G_2G_5^2(G_3+G_4)}{(1+G_1G_2H_1)\lbrace 1+(G_3+G_4)G_5H_3\rbrace G_5-G_1G_2G_5(G_3+G_4)H_2}$$

Note − 여러 입력이있는 블록 다이어그램의 전달 함수를 계산하려면 다음 단계를 따르십시오.

• Step 1 − 한 번에 하나의 입력을 고려하여 블록 다이어그램의 전달 함수를 찾고 나머지 입력을 0으로 만듭니다.

• Step 2 − 나머지 입력에 대해 1 단계를 반복합니다.

• Step 3 − 모든 전달 함수를 추가하여 전체 전달 함수를 얻습니다.

블록 다이어그램 축소 프로세스는 복잡한 시스템의 경우 더 많은 시간이 걸립니다. 왜냐하면 각 단계 후에 (부분적으로 단순화 된) 블록 다이어그램을 그려야하기 때문입니다. 따라서 이러한 단점을 극복하려면 신호 흐름 그래프 (표현)를 사용하십시오.

다음 두 장에서는 신호 흐름 그래프와 관련된 개념, 즉 주어진 블록 다이어그램에서 신호 흐름 그래프를 표현하는 방법과 감소 프로세스를 수행하지 않고 이득 공식을 사용하여 전달 함수를 계산하는 방법에 대해 설명합니다.

신호 흐름 그래프는 대수 방정식의 그래픽 표현입니다. 이 장에서는 신호 흐름 그래프와 관련된 기본 개념에 대해 논의하고 신호 흐름 그래프를 그리는 방법도 알아 봅니다.

신호 흐름 그래프의 기본 요소

노드와 분기는 신호 흐름 그래프의 기본 요소입니다.

마디

Node변수 또는 신호를 나타내는 점입니다. 노드에는 입력 노드, 출력 노드 및 혼합 노드의 세 가지 유형이 있습니다.

• Input Node − 나가는 분기 만있는 노드입니다.

• Output Node − 들어오는 분기 만있는 노드입니다.

• Mixed Node − 들어오는 분기와 나가는 분기가 모두있는 노드입니다.

예

이러한 노드를 식별하기 위해 다음 신호 흐름 그래프를 고려해 보겠습니다.

• 그만큼 nodes 이 신호 흐름 그래프에있는 것은 y₁, y₂, y₃ 과 y₄.

• y₁ 과 y₄ 입니다 input node 과 output node 각기.

• y₂ 과 y₃ 아르 mixed nodes.

분기

Branch두 노드를 연결하는 선분입니다. 둘 다있다gain 과 direction. 예를 들어, 위의 신호 흐름 그래프에는 4 개의 분기가 있습니다. 이 지점은gains 의 a, b, c 과 -d.

신호 흐름 그래프의 구성

다음 대수 방정식을 고려하여 신호 흐름 그래프를 구성 해 보겠습니다.

$$y_2=a_{12}y_1+a_{42}y_4$$

$$y_3=a_{23}y_2+a_{53}y_5$$

$$y_4=a_{34}y_3$$

$$y_5=a_{45}y_4+a_{35}y_3$$

$$y_6=a_{56}y_5$$

여섯이 될 것입니다 nodes(y ₁ , y ₂ , y ₃ , y ₄ , y ₅ 및 y ₆ ) 및 8branches이 신호 흐름 그래프에서. 가지의 이득은 a ₁₂ , a ₂₃ , a ₃₄ , a ₄₅ , a ₅₆ , a ₄₂ , a ₅₃ 및 a ₃₅ 입니다.

전체 신호 흐름 그래프를 얻으려면 각 방정식에 대한 신호 흐름 그래프를 그린 다음 이러한 모든 신호 흐름 그래프를 결합한 다음 아래에 주어진 단계를 따르십시오.

Step 1 − 신호 흐름 그래프 $y_2 = a_{13}y_1 + a_{42}y_4$ 다음 그림에 나와 있습니다.

Step 2 − 신호 흐름 그래프 $y_3 = a_{23}y_2 + a_{53}y_5$ 다음 그림에 나와 있습니다.

Step 3 − 신호 흐름 그래프 $y_4 = a_{34}y_3$ 다음 그림에 나와 있습니다.

Step 4 − 신호 흐름 그래프 $y_5 = a_{45}y_4 + a_{35}y_3$ 다음 그림에 나와 있습니다.

Step 5 − 신호 흐름 그래프 $y_6 = a_{56}y_5$ 다음 그림에 나와 있습니다.

Step 6 − 전체 시스템의 신호 흐름 그래프는 다음 그림과 같습니다.

블록 다이어그램을 신호 흐름 그래프로 변환

Follow these steps for converting a block diagram into its equivalent signal flow graph.

• Represent all the signals, variables, summing points and take-off points of block diagram as nodes in signal flow graph.

• Represent the blocks of block diagram as branches in signal flow graph.

• Represent the transfer functions inside the blocks of block diagram as gains of the branches in signal flow graph.

• Connect the nodes as per the block diagram. If there is connection between two nodes (but there is no block in between), then represent the gain of the branch as one. For example, between summing points, between summing point and takeoff point, between input and summing point, between take-off point and output.

예

다음 블록 다이어그램을 동등한 신호 흐름 그래프로 변환 해 보겠습니다.

입력 신호를 나타냅니다. $R(s)$ 및 출력 신호 $C(s)$ 블록 다이어그램을 입력 노드로 $R(s)$ 및 출력 노드 $C(s)$ 신호 흐름 그래프의.

참고로, 나머지 노드 (y ₁ ~ y ₉ )는 블록 다이어그램에서 레이블이 지정됩니다. 입력 및 출력 노드 외에 9 개의 노드가 있습니다. 즉, 4 개의 합산 지점에 대한 4 개의 노드, 4 개의 이륙 지점에 대한 4 개의 노드, 블록 간 변수에 대한 1 개의 노드입니다.$G_1$ 과 $G_2$.

다음 그림은 등가 신호 흐름 그래프를 보여줍니다.

Mason의 이득 공식 (다음 장에서 설명)을 사용하여이 신호 흐름 그래프의 전달 함수를 계산할 수 있습니다. 이것이 신호 흐름 그래프의 장점입니다. 여기서 전달 함수를 계산하기 위해 신호 흐름 그래프를 단순화 (축소) 할 필요가 없습니다.

이제 메이슨의 이득 공식에 대해 논의하겠습니다. 신호 흐름 그래프에 'N'순방향 경로가 있다고 가정합니다. 신호 흐름 그래프의 입력 노드와 출력 노드 사이의 이득은transfer function시스템의. Mason의 이득 공식을 사용하여 계산할 수 있습니다.

Mason’s gain formula is

$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^N _{i=1}P_i\Delta _i}{\Delta}$$

어디,

• C(s) 출력 노드입니다.

• R(s) 입력 노드입니다.

• T 전달 함수 또는 이득 $R(s)$ 과 $C(s)$

• P_ii ^번째 순방향 경로 이득

$\Delta =1-(sum \: of \: all \: individual \: loop \: gains)$

$+(sum \: of \: gain \: products \: of \: all \: possible \: two \:nontouching \: loops)$

$$-(sum \: of \: gain \: products \: of \: all \: possible \: three \: nontouching \: loops)+...$$

Δ _i 는 i ^번째 순방향 경로에 닿는 루프를 제거하여 Δ에서 얻습니다 .

여기에 포함 된 기본 용어를 이해하려면 다음 신호 흐름 그래프를 고려하십시오.

통로

분기 화살표 방향으로 한 노드에서 다른 노드로 분기를 순회하는 것입니다. 노드를 두 번 이상 통과해서는 안됩니다.

Examples − $y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5$ 과 $y_5 \rightarrow y_3 \rightarrow y_2$

앞으로 경로

입력 노드에서 출력 노드까지 존재하는 경로는 다음과 같습니다. forward path.

Examples − $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ 과 $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$.

순방향 경로 이득

순방향 경로의 모든 분기 이득의 곱을 계산하여 얻습니다.

Examples − $abcde$ 순방향 경로 이득입니다 $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ abge는 순방향 경로 이득입니다. $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$.

고리

한 노드에서 시작하여 동일한 노드에서 끝나는 경로를 loop. 따라서 그것은 닫힌 경로입니다.

Examples − $y_2 \rightarrow y_3 \rightarrow y_2$ 과 $y_3 \rightarrow y_5 \rightarrow y_3$.

루프 이득

루프의 모든 분기 이득의 곱을 계산하여 얻습니다.

Examples − $b_j$ 루프 이득 $y_2 \rightarrow y_3 \rightarrow y_2$ 과 $g_h$ 루프 이득 $y_3 \rightarrow y_5 \rightarrow y_3$.

비접촉 루프

공통 노드가 없어야하는 루프입니다.

Examples − 루프, $y_2 \rightarrow y_3 \rightarrow y_2$ 과 $y_4 \rightarrow y_5 \rightarrow y_4$ 건드리지 않습니다.

Mason의 이득 공식을 사용한 전달 함수 계산

전달 함수를 찾기 위해 동일한 신호 흐름 그래프를 고려해 보겠습니다.

• 순방향 경로 수, N = 2.

• 첫 번째 전진 경로는- $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$.

• 첫 번째 순방향 경로 이득, $p_1 = abcde$.

• 두 번째 전진 경로는- $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$.

• 두 번째 순방향 경로 이득, $p_2 = abge$.

• 개별 루프 수, L = 5.

• 루프는- $y_2 \rightarrow y_3 \rightarrow y_2$, $y_3 \rightarrow y_5 \rightarrow y_3$, $y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_3$, $y_4 \rightarrow y_5 \rightarrow y_4$ 과 $y_5 \rightarrow y_5$.

• 루프 이득은- $l_1 = bj$, $l_2 = gh$, $l_3 = cdh$, $l_4 = di$ 과 $l_5 = f$.

• 두 개의 비접촉 루프 수 = 2.

• 첫 번째 비접촉 루프 쌍은- $y_2 \rightarrow y_3 \rightarrow y_2$, $y_4 \rightarrow y_5 \rightarrow y_4$.

• 첫 번째 비접촉 루프 쌍의 곱을 얻고, $l_1l_4 = bjdi$

• 두 번째 비접촉 루프 쌍은- $y_2 \rightarrow y_3 \rightarrow y_2$, $y_5 \rightarrow y_5$.

• 두 번째 비접촉 루프 쌍의 이득 곱은- $l_1l_5 = bjf$

이 신호 흐름 그래프에는 더 많은 수 (2 개 이상의) 비접촉 루프가 없습니다.

우린 알아,

$\Delta =1-(sum \: of \: all \: individual \: loop \: gains)$

$+(sum \: of \: gain \: products \: of \: all \: possible \: two \:nontouching \: loops)$

$$-(sum \: of \: gain \: products \: of \: all \: possible \: three \: nontouching \: loops)+...$$

위 방정식의 값을 대체하십시오.

$\Delta =1-(bj+gh+cdh+di+f)+(bjdi+bjf)-(0)$

$\Rightarrow \Delta=1-(bj+gh+cdh+di+f)+bjdi+bjf$

첫 번째 순방향 경로를 건드리지 않는 루프가 없습니다.

그래서, $\Delta_1=1$.

비슷하게, $\Delta_2=1$. 이후 두 번째 순방향 경로를 건드리지 않는 루프가 없습니다.

대입, Mason의 이득 공식에서 N = 2

$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^2 _{i=1}P_i\Delta _i}{\Delta}$$

$$T=\frac{C(s)}{R(s)}=\frac{P_1\Delta_1+P_2\Delta_2}{\Delta}$$

위의 방정식에서 필요한 모든 값을 대체하십시오.

$$T=\frac{C(s)}{R(s)}=\frac{(abcde)1+(abge)1}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$

$$\Rightarrow T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$

따라서 전달 함수는-

$$T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$

시간 영역과 주파수 영역 모두에서 제어 시스템의 응답을 분석 할 수 있습니다. 이후 장에서 제어 시스템의 주파수 응답 분석에 대해 설명합니다. 이제 제어 시스템의 시간 응답 분석에 대해 논의하겠습니다.

시간 응답이란 무엇입니까?

입력에 대한 제어 시스템의 출력이 시간에 따라 변하면 time response제어 시스템의. 시간 응답은 두 부분으로 구성됩니다.

• 일시적인 응답
• 정상 상태 응답

시간 영역에서 제어 시스템의 응답은 다음 그림과 같습니다.

여기에서 과도 및 정상 상태가 그림에 표시됩니다. 이러한 상태에 해당하는 응답을 과도 및 정상 상태 응답이라고합니다.

수학적으로 시간 응답 c (t)를 다음과 같이 작성할 수 있습니다.

$$c(t)=c_{tr}(t)+c_{ss}(t)$$

어디,

• c _tr (t)는 과도 응답입니다.
• C의 _SS (t)는 정상 상태 반응이다

과도 응답

제어 시스템에 입력을 적용한 후 출력이 정상 상태에 도달하는 데 일정 시간이 걸립니다. 따라서 출력은 정상 상태가 될 때까지 일시적인 상태가됩니다. 따라서 과도 상태에서 제어 시스템의 응답은 다음과 같이 알려져 있습니다.transient response.

과도 응답은 't'값이 큰 경우 0이됩니다. 이상적으로이 't'값은 무한대이며 실제로는 5 배 상수입니다.

수학적으로 다음과 같이 쓸 수 있습니다.

$$\lim_{t\rightarrow \infty }c_{tr}(t)=0$$

정상 상태 응답

과도 응답이 큰 't'값에 대해 값이 0 인 후에도 남아있는 시간 응답 부분은 다음과 같이 알려져 있습니다. steady state response. 즉, 정상 상태에서도 과도 응답이 0이됩니다.

Example

제어 시스템의 시간 응답에 대한 과도 및 정상 상태 조건을 찾아 보겠습니다. $c(t)=10+5e^{-t}$

여기, 두 번째 학기 $5e^{-t}$ 0이 될 것입니다 t무한대를 나타냅니다. 그래서 이것은transient term. 그리고 첫 번째 학기 10은t무한에 접근합니다. 그래서 이것은steady state term.

표준 테스트 신호

표준 테스트 신호는 임펄스, 스텝, 램프 및 포물선입니다. 이러한 신호는 출력의 시간 응답을 사용하여 제어 시스템의 성능을 파악하는 데 사용됩니다.

단위 임펄스 신호

단위 임펄스 신호, δ (t)는 다음과 같이 정의됩니다.

$\delta (t)=0$ ...에 대한 $t\neq 0$

과 $\int_{0^-}^{0^+} \delta (t)dt=1$

다음 그림은 단위 임펄스 신호를 보여줍니다.

따라서 단위 임펄스 신호는 't'가 0 일 때만 존재합니다. 't'주변의 작은 시간 간격에서이 신호의 면적은 0과 같습니다. 단위 임펄스 신호의 값은 't'의 다른 모든 값에 대해 0입니다.

단위 단계 신호

단위 단계 신호 u (t)는 다음과 같이 정의됩니다.

$$u(t)=1;t\geq 0$$

$=0; t<0$

다음 그림은 단위 단계 신호를 보여줍니다.

따라서 단위 스텝 신호는 0을 포함한 모든 양의 't'값에 대해 존재합니다. 그리고 그 값은이 간격 동안 1입니다. 단위 스텝 신호의 값은 't'의 모든 음수 값에 대해 0입니다.

단위 램프 신호

단위 램프 신호, r (t)는 다음과 같이 정의됩니다.

$$r(t)=t; t\geq 0$$

$=0; t<0$

단위 램프 신호를 쓸 수 있습니다. $r(t)$ 단위 스텝 신호로 $u(t)$ 같이

$$r(t)=tu(t)$$

다음 그림은 단위 램프 신호를 보여줍니다.

따라서 단위 램프 신호는 0을 포함한 't'의 모든 양의 값에 대해 존재합니다. 그리고 그 값은이 간격 동안 't'에 대해 선형 적으로 증가합니다. 단위 램프 신호의 값은 't'의 모든 음수 값에 대해 0입니다.

단위 포물선 신호

단위 포물선 신호 p (t)는 다음과 같이 정의됩니다.

$$p(t)=\frac{t^2}{2}; t\geq 0$$

$=0; t<0$

단위 포물선 신호를 쓸 수 있습니다. $p(t)$ 단위 스텝 신호와 관련하여 $u(t)$ 같이,

$$p(t)=\frac{t^2}{2}u(t)$$

다음 그림은 단위 포물선 신호를 보여줍니다.

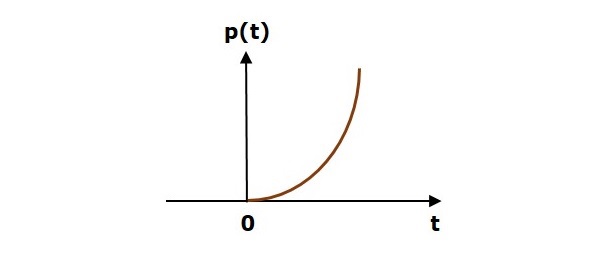
따라서 단위 포물선 신호는 모든 양의 값에 대해 존재합니다. ‘t’0을 포함합니다. 그리고 그 값은이 간격 동안 't'에 대해 비선형 적으로 증가합니다. 단위 포물선 신호의 값은 't'의 모든 음수 값에 대해 0입니다.

이 장에서는 1 차 주문 시스템의 시간 응답에 대해 설명하겠습니다. 폐쇄 루프 제어 시스템의 다음 블록 다이어그램을 고려하십시오. 여기에서 개방 루프 전달 함수는$\frac{1}{sT}$ 통합 부정적인 피드백과 연결됩니다.

우리는 폐쇄 루프 제어 시스템의 전달 함수가 다음과 같이 단일 네거티브 피드백을 갖는다는 것을 알고 있습니다.

$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$

대용품, $G(s)=\frac{1}{sT}$ 위의 방정식에서.

$$\frac{C(s)}{R(s)}=\frac{\frac{1}{sT}}{1+\frac{1}{sT}}=\frac{1}{sT+1}$$

s의 거듭 제곱은 분모 항에서 1입니다. 따라서 위의 전달 함수는 첫 번째 순서이며 시스템은first order system.

위의 방정식을 다음과 같이 다시 작성할 수 있습니다.

$$C(s)=\left ( \frac{1}{sT+1} \right )R(s)$$

어디,

• C(s) 출력 신호 c (t)의 라플라스 변환입니다.

• R(s) 입력 신호 r (t)의 라플라스 변환이고,

• T 시간 상수입니다.

시간 도메인에서 1 차 주문 시스템의 응답 (출력)을 얻으려면 다음 단계를 따르십시오.

• 입력 신호의 라플라스 변환 가져 오기 $r(t)$.

• 방정식을 고려하십시오. $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

• 대용품 $R(s)$ 위 방정식의 값.

• 부분 분수 수행 $C(s)$ 필요한 경우.

• 역 라플라스 변환 적용 $C(s)$.

이전 장에서 우리는 임펄스, 스텝, 램프 및 포물선과 같은 표준 테스트 신호를 보았습니다. 이제 각 입력에 대한 첫 번째 주문 시스템의 응답을 하나씩 알아 보겠습니다. 응답의 이름은 입력 신호의 이름에 따라 제공됩니다. 예를 들어, 임펄스 입력에 대한 시스템의 응답을 임펄스 응답이라고합니다.

1 차 시스템의 임펄스 응답

고려하다 unit impulse signal 1 차 주문 시스템에 대한 입력으로.

그래서, $r(t)=\delta (t)$

양쪽에 라플라스 변환을 적용합니다.

$R(s)=1$

방정식을 고려하십시오. $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

대용품, $R(s) = 1$ 위의 방정식에서.

$$C(s)=\left ( \frac{1}{sT+1} \right )(1)=\frac{1}{sT+1}$$

라플라스 변환의 표준 형식 중 하나로 위의 방정식을 재정렬하십시오.

$$C(s)=\frac{1}{T\left (\ s+\frac{1}{T} \right )} \Rightarrow C(s)=\frac{1}{T}\left ( \frac{1}{s+\frac{1}{T}} \right )$$

양쪽에 역 라플라스 변환을 적용합니다.

$$c(t)=\frac{1}{T}e^\left ( {-\frac{t}{T}} \right )u(t)$$

단위 임펄스 응답은 다음 그림에 나와 있습니다.

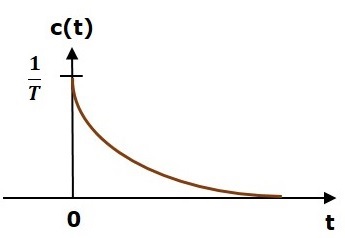
그만큼 unit impulse response, c (t)는 't'의 양수 값에 대한 지수 감쇠 신호이고 't'의 음수 값에 대해서는 0입니다.

첫 주문 시스템의 단계 응답

고려하다 unit step signal 첫 주문 시스템에 대한 입력으로.

그래서, $r(t)=u(t)$

양쪽에 라플라스 변환을 적용합니다.

$$R(s)=\frac{1}{s}$$

방정식을 고려하십시오. $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

대용품, $R(s)=\frac{1}{s}$ 위의 방정식에서.

$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s} \right )=\frac{1}{s\left ( sT+1 \right )}$$

C (s)의 부분 분수를 수행합니다.

$$C(s)=\frac{1}{s\left ( sT+1 \right )}=\frac{A}{s}+\frac{B}{sT+1}$$

$$\Rightarrow \frac{1}{s\left ( sT+1 \right )}=\frac{A\left ( sT+1 \right )+Bs}{s\left ( sT+1 \right )}$$

양쪽에서 분모 용어는 동일합니다. 따라서 서로에 의해 취소됩니다. 따라서 분자 항을 동일시하십시오.

$$1=A\left ( sT+1 \right )+Bs$$

양쪽의 상수 항을 동일시하면 A = 1이됩니다.

A = 1을 대입하고 계수를 동일시하십시오. s 양쪽의 용어.

$$0=T+B \Rightarrow B=-T$$

대입, A = 1 및 B = −T의 부분 분수 전개 $C(s)$.

$$C(s)=\frac{1}{s}-\frac{T}{sT+1}=\frac{1}{s}-\frac{T}{T\left ( s+\frac{1}{T} \right )}$$

$$\Rightarrow C(s)=\frac{1}{s}-\frac{1}{s+\frac{1}{T}}$$

양쪽에 역 라플라스 변환을 적용합니다.

$$c(t)=\left ( 1-e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$

그만큼 unit step response, c (t)에는 과도 및 정상 상태 항이 모두 있습니다.

단위 단계 응답의 과도 조건은 다음과 같습니다.

$$c_{tr}(t)=-e^{-\left ( \frac{t}{T} \right )}u(t)$$

단위 단계 응답의 정상 상태 용어는 다음과 같습니다.

$$c_{ss}(t)=u(t)$$

다음 그림은 단위 단계 응답을 보여줍니다.

가치 unit step response, c(t)t = 0 및 t의 모든 음수 값에서 0입니다. 0에서 점차적으로 증가하고 마침내 정상 상태에서 1에 도달합니다. 따라서 정상 상태 값은 입력의 크기에 따라 달라집니다.

1 차 주문 시스템의 램프 응답

고려하다 unit ramp signal 1 차 주문 시스템에 대한 입력으로.

$So, r(t)=tu(t)$

양쪽에 라플라스 변환을 적용합니다.

$$R(s)=\frac{1}{s^2}$$

방정식을 고려하십시오. $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

대용품, $R(s)=\frac{1}{s^2}$ 위의 방정식에서.

$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s^2} \right )=\frac{1}{s^2(sT+1)}$$

부분 분수 수행 $C(s)$.

$$C(s)=\frac{1}{s^2(sT+1)}=\frac{A}{s^2}+\frac{B}{s}+\frac{C}{sT+1}$$

$$\Rightarrow \frac{1}{s^2(sT+1)}=\frac{A(sT+1)+Bs(sT+1)+Cs^2}{s^2(sT+1)}$$

양쪽에서 분모 용어는 동일합니다. 따라서 서로에 의해 취소됩니다. 따라서 분자 항을 동일시하십시오.

$$1=A(sT+1)+Bs(sT+1)+Cs^2$$

양쪽의 상수 항을 동일시하면 A = 1이됩니다.

A = 1을 대입하고 양쪽에있는 s 항의 계수를 동일시하십시오.

$$0=T+B \Rightarrow B=-T$$

유사하게, B = −T로 대입하고 계수를 동일시하십시오. $s^2$양쪽의 용어. 당신은 얻을 것이다$C=T^2$.

A = 1, B = −T 및 $C = T^2$ 부분 분수 확장에서 $C(s)$.

$$C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{sT+1}=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{T\left ( s+\frac{1}{T} \right )}$$

$$\Rightarrow C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T}{s+\frac{1}{T}}$$

양쪽에 역 라플라스 변환을 적용합니다.

$$c(t)=\left ( t-T+Te^{-\left ( \frac{t}{T} \right )} \right )u(t)$$

그만큼 unit ramp response, c (t)에는 과도 및 정상 상태 항이 모두 있습니다.

단위 램프 응답의 과도 조건은 다음과 같습니다.

$$c_{tr}(t)=Te^{-\left ( \frac{t}{T} \right )}u(t)$$

단위 램프 응답의 정상 상태 용어는 다음과 같습니다.

$$c_{ss}(t)=(t-T)u(t)$$

다음 그림은 단위 램프 응답을 보여줍니다.

그만큼 unit ramp response, c (t)는 t의 모든 양수 값에 대해 단위 램프 입력 신호를 따릅니다. 그러나 입력 신호에서 T 단위의 편차가 있습니다.

1 차 시스템의 포물선 응답

고려하다 unit parabolic signal 1 차 주문 시스템에 대한 입력으로.

그래서, $r(t)=\frac{t^2}{2}u(t)$

양쪽에 라플라스 변환을 적용합니다.

$$R(s)=\frac{1}{s^3}$$

방정식을 고려하십시오. $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

대용품 $R(s)=\frac{1}{s^3}$ 위의 방정식에서.

$$C(s)=\left ( \frac{1}{sT+1} \right )\left( \frac{1}{s^3} \right )=\frac{1}{s^3(sT+1)}$$

부분 분수 수행 $C(s)$.

$$C(s)=\frac{1}{s^3(sT+1)}=\frac{A}{s^3}+\frac{B}{s^2}+\frac{C}{s}+\frac{D}{sT+1}$$

단순화 한 후 A, B, C 및 D의 값을 1로 얻습니다. $-T, \: T^2\: and \: −T^3$각기. 위의 C (s)의 부분 분수 전개에서이 값을 대체하십시오.

$C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^3}{sT+1} \: \Rightarrow C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^2}{s+\frac{1}{T}}$

양쪽에 역 라플라스 변환을 적용합니다.

$$c(t)=\left ( \frac{t^2}{2} -Tt+T^2-T^2e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$

그만큼 unit parabolic response, c (t)에는 과도 및 정상 상태 항이 모두 있습니다.

단위 포물선 응답의 과도 항은 다음과 같습니다.

$$C_{tr}(t)=-T^2e^{-\left ( \frac{t}{T} \right )}u(t)$$

단위 포물선 응답의 정상 상태 항은 다음과 같습니다.

$$C_{ss}(t)=\left ( \frac{t^2}{2} -Tt+T^2 \right )u(t)$$

이러한 응답으로부터 우리는 1 차 제어 시스템이 램프 및 포물선 형 입력으로 안정적이지 않다는 결론을 내릴 수 있습니다. 이러한 응답은 무한한 시간에도 계속 증가하기 때문입니다. 1 차 제어 시스템은 이러한 응답이 제한된 출력을 갖기 때문에 임펄스 및 단계 입력으로 안정적입니다. 그러나 임펄스 응답에는 정상 상태 항이 없습니다. 따라서 단계 신호는 응답으로부터 제어 시스템을 분석하기 위해 시간 영역에서 널리 사용됩니다.

이 장에서는 2 차 주문 시스템의 시간 응답에 대해 설명하겠습니다. 폐쇄 루프 제어 시스템의 다음 블록 다이어그램을 고려하십시오. 여기에서 개방 루프 전달 함수는$\frac{\omega ^2_n}{s(s+2\delta \omega_n)}$ 통합 부정적인 피드백과 연결됩니다.

유니티 네거티브 피드백을 갖는 폐쇄 루프 제어 시스템의 전달 함수는 다음과 같습니다.

$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$

대용품, $G(s)=\frac{\omega ^2_n}{s(s+2\delta \omega_n)}$ 위의 방정식에서.

$$\frac{C(s)}{R(s)}=\frac{\left (\frac{\omega ^2_n}{s(s+2\delta \omega_n)} \right )}{1+ \left ( \frac{\omega ^2_n}{s(s+2\delta \omega_n)} \right )}=\frac{\omega _n^2}{s^2+2\delta \omega _ns+\omega _n^2}$$

's'의 거듭 제곱은 분모 항에서 2입니다. 따라서 위의 전달 함수는 2 차이며 시스템은second order system.

특성 방정식은-

$$s^2+2\delta \omega _ns+\omega _n^2=0$$

특성 방정식의 뿌리는 다음과 같습니다.

$$s=\frac{-2\omega \delta _n\pm \sqrt{(2\delta\omega _n)^2-4\omega _n^2}}{2}=\frac{-2(\delta\omega _n\pm \omega _n\sqrt{\delta ^2-1})}{2}$$

$$\Rightarrow s=-\delta \omega_n \pm \omega _n\sqrt{\delta ^2-1}$$

• 두 근은 δ = 0 일 때 허수입니다.
• 두 근은 실수이며 δ = 1 일 때 동일합니다.
• 두 근은 실수이지만 δ> 1 일 때 같지 않습니다.
• 두 뿌리는 0 <δ <1 일 때 복합 켤레입니다.

우리는 쓸 수있다 $C(s)$ 방정식으로,

$$C(s)=\left ( \frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2} \right )R(s)$$

어디,

• C(s) 출력 신호 c (t)의 라플라스 변환입니다.

• R(s) 입력 신호의 라플라스 변환 r (t)

• ω_n 고유 진동수

• δ 감쇠비입니다.

시간 도메인에서 2 차 시스템의 응답 (출력)을 얻으려면 다음 단계를 따르십시오.

• 입력 신호의 라플라스 변환을 취하십시오. $r(t)$.

• 방정식을 고려하십시오. $C(s)=\left ( \frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2} \right )R(s)$

• 대용품 $R(s)$ 위 방정식의 값.

• 부분 분수 수행 $C(s)$ 필요한 경우.

• 역 라플라스 변환 적용 $C(s)$.

2 차 주문 시스템의 단계 응답

단위 단계 신호를 2 차 시스템에 대한 입력으로 고려하십시오.

단위 스텝 신호의 라플라스 변환은,

$$R(s)=\frac{1}{s}$$

2 차 폐 루프 제어 시스템의 전달 함수는 다음과 같습니다.

$$\frac{C(s)}{R(s)}=\frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$

사례 1 : δ = 0

대용품, $\delta = 0$ 전달 함수에서.

$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+\omega_n^2}$$

$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{s^2+\omega_n^2} \right )R(s)$$

대용품, $R(s) = \frac{1}{s}$ 위의 방정식에서.

$$C(s)=\left( \frac{\omega_n^2}{s^2+\omega_n^2} \right )\left( \frac{1}{s} \right )=\frac{\omega_n^2}{s(s^2+\omega_n^2)}$$

양쪽에 역 라플라스 변환을 적용합니다.

$$c(t)=\left ( 1-\cos(\omega_n t) \right )u(t)$$

따라서 2 차 주문 시스템의 단위 단계 응답은 $/delta = 0$ 진폭과 주파수가 일정한 연속 시간 신호가됩니다.

사례 2 : δ = 1

대용품, $/delta = 1$ 전달 함수에서.

$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+2\omega_ns+\omega_n^2}$$

$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{(s+\omega_n)^2} \right)R(s)$$

대용품, $R(s) = \frac{1}{s}$ 위의 방정식에서.

$$C(s)=\left( \frac{\omega_n^2}{(s+\omega_n)^2} \right)\left ( \frac{1}{s} \right)=\frac{\omega_n^2}{s(s+\omega_n)^2}$$

부분 분수 수행 $C(s)$.

$$C(s)=\frac{\omega_n^2}{s(s+\omega_n)^2}=\frac{A}{s}+\frac{B}{s+\omega_n}+\frac{C}{(s+\omega_n)^2}$$

단순화 한 후 A, B 및 C의 값을 다음과 같이 얻습니다. $1,\: -1\: and \: −\omega _n$각기. 위의 부분 분수 확장에서 이러한 값을 대체하십시오.$C(s)$.

$$C(s)=\frac{1}{s}-\frac{1}{s+\omega_n}-\frac{\omega_n}{(s+\omega_n)^2}$$

양쪽에 역 라플라스 변환을 적용합니다.

$$c(t)=(1-e^{-\omega_nt}-\omega _nte^{-\omega_nt})u(t)$$

따라서 2 차 시스템의 단위 스텝 응답은 정상 상태에서 스텝 입력에 도달하려고합니다.

사례 3 : 0 <δ <1

전달 함수의 분모 항을 다음과 같이 수정할 수 있습니다.

$$s^2+2\delta\omega_ns+\omega_n^2=\left \{ s^2+2(s)(\delta \omega_n)+(\delta \omega_n)^2 \right \}+\omega_n^2-(\delta\omega_n)^2$$

$$=(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)$$

전달 함수는 다음과 같습니다.

$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$

$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)} \right )R(s)$$

대용품, $R(s) = \frac{1}{s}$ 위의 방정식에서.

$$C(s)=\left( \frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)} \right )\left( \frac{1}{s} \right )=\frac{\omega_n^2}{s\left ((s+\delta\omega_n)^2+\omega_n^2(1-\delta^2) \right)}$$

부분 분수 수행 $C(s)$.

$$C(s)=\frac{\omega_n^2}{s\left ((s+\delta\omega_n)^2+\omega_n^2(1-\delta^2) \right)}=\frac{A}{s}+\frac{Bs+C}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$

단순화 한 후 A, B 및 C의 값을 다음과 같이 얻습니다. $1,\: -1 \: and \: −2\delta \omega _n$각기. 위의 C (s)의 부분 분수 전개에서이 값을 대체하십시오.

$$C(s)=\frac{1}{s}-\frac{s+2\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$

$$C(s)=\frac{1}{s}-\frac{s+\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}-\frac{\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$

$C(s)=\frac{1}{s}-\frac{(s+\delta\omega_n)}{(s+\delta\omega_n)^2+(\omega_n\sqrt{1-\delta^2})^2}-\frac{\delta}{\sqrt{1-\delta^2}}\left ( \frac{\omega_n\sqrt{1-\delta^2}}{(s+\delta\omega_n)^2+(\omega_n\sqrt{1-\delta^2})^2} \right )$

대용품, $\omega_n\sqrt{1-\delta^2}$ 같이 $\omega_d$ 위의 방정식에서.

$$C(s)=\frac{1}{s}-\frac{(s+\delta\omega_n)}{(s+\delta\omega_n)^2+\omega_d^2}-\frac{\delta}{\sqrt{1-\delta^2}}\left ( \frac{\omega_d}{(s+\delta\omega_n)^2+\omega_d^2} \right )$$

양쪽에 역 라플라스 변환을 적용합니다.

$$c(t)=\left ( 1-e^{-\delta \omega_nt}\cos(\omega_dt)-\frac{\delta}{\sqrt{1-\delta^2}}e^{-\delta\omega_nt}\sin(\omega_dt) \right )u(t)$$

$$c(t)=\left ( 1-\frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}}\left ( (\sqrt{1-\delta^2})\cos(\omega_dt)+\delta \sin(\omega_dt) \right ) \right )u(t)$$

만약 $\sqrt{1-\delta^2}=\sin(\theta)$이면 'δ'는 cos (θ)가됩니다. 위의 방정식에서 이러한 값을 대체하십시오.

$$c(t)=\left ( 1-\frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}}(\sin(\theta)\cos(\omega_dt)+\cos(\theta)\sin(\omega_dt)) \right )u(t)$$

$$\Rightarrow c(t)=\left ( 1-\left ( \frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta) \right )u(t)$$

따라서 2 차 시스템의 단위 스텝 응답은 'δ'가 0과 1 사이에있을 때 감쇠 진동 (진폭 감소)을가집니다.

사례 4 : δ> 1

전달 함수의 분모 항을 다음과 같이 수정할 수 있습니다.

$$s^2+2\delta\omega_ns+\omega_n^2=\left \{ s^2+2(s)(\delta\omega_n)+(\delta\omega_n)^2 \right \}+\omega_n^2-(\delta\omega_n)^2$$

$$=\left ( s+\delta\omega_n \right )^2-\omega_n^2\left ( \delta^2-1 \right )$$

전달 함수는 다음과 같습니다.

$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{(s+\delta\omega_n)^2-\omega_n^2(\delta^2-1)}$$

$$\Rightarrow C(s)=\left ( \frac{\omega_n^2}{(s+\delta\omega_n)^2-\omega_n^2(\delta^2-1)} \right )R(s)$$

대용품, $R(s) = \frac{1}{s}$ 위의 방정식에서.

$C(s)=\left ( \frac{\omega_n^2}{(s+\delta\omega_n)^2-(\omega_n\sqrt{\delta^2-1})^2} \right )\left ( \frac{1}{s} \right )=\frac{\omega_n^2}{s(s+\delta\omega_n+\omega_n\sqrt{\delta^2-1})(s+\delta\omega_n-\omega_n\sqrt{\delta^2-1})}$

부분 분수 수행 $C(s)$.

$$C(s)=\frac{\omega_n^2}{s(s+\delta\omega_n+\omega_n\sqrt{\delta^2-1})(s+\delta\omega_n-\omega_n\sqrt{\delta^2-1})}$$

$$=\frac{A}{s}+\frac{B}{s+\delta\omega_n+\omega_n\sqrt{\delta^2-1}}+\frac{C}{s+\delta\omega_n-\omega_n\sqrt{\delta^2-1}}$$

단순화 한 후 A, B 및 C의 값을 1로 얻습니다. $\frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}$ 과 $\frac{-1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}$각기. 위의 부분 분수 확장에서 이러한 값을 대체하십시오.$C(s)$.

$$C(s)=\frac{1}{s}+\frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}\left ( \frac{1}{s+\delta\omega_n+\omega_n\sqrt{\delta^2-1}} \right )-\left ( \frac{1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )\left ( \frac{1}{s+\delta\omega_n-\omega_n\sqrt{\delta^2-1}} \right )$$

양쪽에 역 라플라스 변환을 적용합니다.

$c(t)=\left ( 1+\left ( \frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )e^{-(\delta\omega_n+\omega_n\sqrt{\delta^2-1})t}-\left ( \frac{1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )e^{-(\delta\omega_n-\omega_n\sqrt{\delta^2-1})t} \right )u(t)$

과도하게 감쇠 되었기 때문에 δ> 1 일 때 2 차 시스템의 단위 스텝 응답은 정상 상태에서 스텝 입력에 도달하지 않습니다.

2 차 시스템의 임펄스 응답

그만큼 impulse response 이 두 가지 방법 중 하나를 사용하여 2 차 주문 시스템을 얻을 수 있습니다.

• 값을 고려하여 단계 응답을 도출하면서 관련된 절차를 따르십시오. $R(s)$ 대신 1로 $\frac{1}{s}$.

• 단계 응답의 차별화를 수행하십시오.

다음 표는 감쇠비의 4 가지 경우에 대한 2 차 시스템의 임펄스 응답을 보여줍니다.

감쇠비의 조건	t ≥ 0에 대한 임펄스 응답
δ = 0	$\omega_n\sin(\omega_nt)$
δ = 1	$\omega_n^2te^{-\omega_nt}$
0 <δ <1	$\left ( \frac{\omega_ne^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt)$
δ> 1	$\left ( \frac{\omega_n}{2\sqrt{\delta^2-1}} \right )\left ( e^{-(\delta\omega_n-\omega_n\sqrt{\delta^2-1})t}-e^{-(\delta\omega_n+\omega_n\sqrt{\delta^2-1})t} \right )$

이 장에서는 2 차 시스템의 시간 도메인 사양에 대해 설명합니다. 언더 댐핑 케이스에 대한 2 차 시스템의 단계 응답은 다음 그림에 나와 있습니다.

이 그림에는 모든 시간 도메인 사양이 나와 있습니다. 안정화 시간까지의 응답을 과도 응답이라고하고 안정화 시간 이후의 응답을 정상 상태 응답이라고합니다.

지연 시간

응답이 도달하는 데 필요한 시간입니다. half of its final value제로 순간부터. 다음과 같이 표시됩니다.$t_d$.

'δ'가 0과 1 사이에있을 때 t ≥ 0에 대한 2 차 시스템의 단계 응답을 고려하십시오.

$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$

단계 응답의 최종 값은 1입니다.

따라서 $t=t_d$, 스텝 응답 값은 0.5가됩니다. 위의 방정식에서 이러한 값을 대체하십시오.

$$c(t_d)=0.5=1-\left ( \frac{e^{-\delta\omega_nt_d}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_d+\theta)$$

$$\Rightarrow \left ( \frac{e^{-\delta\omega_nt_d}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_d+\theta)=0.5$$

선형 근사를 사용하면 delay time t_d 같이

$$t_d=\frac{1+0.7\delta}{\omega_n}$$

상승 시간

응답이 상승하는 데 필요한 시간입니다. 0% to 100% of its final value. 이것은under-damped systems. 과감 쇠 시스템의 경우 최종 값의 10 %에서 90 % 사이의 지속 시간을 고려하십시오. 상승 시간은 다음과 같이 표시됩니다.t_r.

t = t ₁ = 0, c (t) = 0에서.

단계 응답의 최종 값은 1이라는 것을 알고 있습니다.

따라서 $t = t_2$, 단계 응답의 값은 1입니다. 다음 방정식에서이 값을 대체하십시오.

$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$

$$c(t_2)=1=1-\left ( \frac{e^{-\delta\omega_nt_2}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_2+\theta)$$

$$\Rightarrow \left ( \frac{e^{-\delta\omega_nt_2}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_2+\theta)=0$$

$$\Rightarrow \sin(\omega_dt_2+\theta)=0$$

$$\Rightarrow \omega_dt_2+\theta=\pi$$

$$\Rightarrow t_2=\frac{\pi-\theta}{\omega_d}$$

다음 방정식에서 t ₁ 및 t ₂ 값을 대체하십시오.rise time,

$$t_r=t_2-t_1$$

$$\therefore \: t_r=\frac{\pi-\theta}{\omega_d}$$

위의 방정식에서 우리는 상승 시간이 $t_r$ 감쇠 된 주파수 $\omega_d$ 서로 반비례합니다.

피크 타임

응답이 도달하는 데 필요한 시간입니다. peak value처음으로. 다음과 같이 표시됩니다.$t_p$. 에서$t = t_p$, 응답의 첫 번째 도함수는 0입니다.

저 감쇠 케이스에 대한 2 차 시스템의 단계 응답은

$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$

구별 짓다 $c(t)$ 't'와 관련하여.

$$\frac{\text{d}c(t)}{\text{d}t}=-\left ( \frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\omega_d\cos(\omega_dt+\theta)-\left ( \frac{-\delta\omega_ne^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$

대용품, $t=t_p$ 과 $\frac{\text{d}c(t)}{\text{d}t}=0$ 위의 방정식에서.

$$0=-\left ( \frac{e^{-\delta\omega_nt_p}}{\sqrt{1-\delta^2}} \right )\left [ \omega_d\cos(\omega_dt_p+\theta)-\delta\omega_n\sin(\omega_dt_p+\theta) \right ]$$

$$\Rightarrow \omega_n\sqrt{1-\delta^2}\cos(\omega_dt_p+\theta)-\delta\omega_n\sin(\omega_dt_p+\theta)=0$$

$$\Rightarrow \sqrt{1-\delta^2}\cos(\omega_dt_p+\theta)-\delta\sin(\omega_dt_p+\theta)=0$$

$$\Rightarrow \sin(\theta)\cos(\omega_dt_p+\theta)-\cos(\theta)\sin(\omega_dt_p+\theta)=0$$

$$\Rightarrow \sin(\theta-\omega_dt_p-\theta)=0$$

$$\Rightarrow sin(-\omega_dt_p)=0\Rightarrow -\sin(\omega_dt_p)=0\Rightarrow sin(\omega_dt_p)=0$$

$$\Rightarrow \omega_dt_p=\pi$$

$$\Rightarrow t_p=\frac{\pi}{\omega_d}$$

위의 방정식에서 우리는 피크 시간이 $t_p$ 감쇠 된 주파수 $\omega_d$ 서로 반비례합니다.

피크 오버 슈트

피크 오버 슈트 M_p응답의 최종 값에서 피크 시간에 응답의 편차로 정의됩니다. 또한maximum overshoot.

수학적으로 다음과 같이 쓸 수 있습니다.

$$M_p=c(t_p)-c(\infty)$$

어디,

c (t _p )는 응답의 피크 값입니다.

c (∞)는 응답의 최종 (안정 상태) 값입니다.

에서 $t = t_p$, 응답 c (t)는-

$$c(t_p)=1-\left ( \frac{e^{-\delta\omega_nt_p}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_p+\theta)$$

대용품, $t_p=\frac{\pi}{\omega_d}$ 위 방정식의 오른쪽에 있습니다.

$$c(t_P)=1-\left ( \frac{e^{-\delta\omega_n\left ( \frac{\pi}{\omega_d} \right )}}{\sqrt{1-\delta^2}} \right )\sin\left ( \omega_d\left ( \frac{\pi}{\omega_d} \right ) +\theta\right )$$

$$\Rightarrow c(t_p)=1-\left ( \frac{e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}}{\sqrt{1-\delta^2}} \right )(-\sin(\theta))$$

우리는 알고 있습니다

$$\sin(\theta)=\sqrt{1-\delta^2}$$

그래서 우리는 얻을 것입니다 $c(t_p)$ 같이

$$c(t_p)=1+e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}$$

값을 대체하십시오. $c(t_p)$ 과 $c(\infty)$ 피크 오버 슈트 방정식에서.

$$M_p=1+e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}-1$$

$$\Rightarrow M_p=e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}$$

Percentage of peak overshoot % $M_p$ 이 공식을 사용하여 계산할 수 있습니다.

$$\%M_p=\frac{M_p}{c(\infty )}\times 100\%$$

값을 대체하여 $M_p$ 과 $c(\infty)$ 위의 공식에서 우리는 피크 오버 슈트의 백분율을 얻을 것입니다 $\%M_p$ 같이

$$\%M_p=\left ( e^ {-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )} \right )\times 100\%$$

위의 방정식에서 우리는 피크 오버 슈트의 비율이 $\% M_p$ 감쇠비가 감소하면 $\delta$ 증가합니다.

정착 시간

응답이 정상 상태에 도달하고 최종 값 주변의 지정된 허용 범위 내에 머무르는 데 필요한 시간입니다. 일반적으로 공차 밴드는 2 % 및 5 %입니다. 정착 시간은 다음과 같이 표시됩니다.$t_s$.

5 % 공차 대역의 안정화 시간은 다음과 같습니다.

$$t_s=\frac{3}{\delta\omega_n}=3\tau$$

2 % 공차 대역의 안정화 시간은 다음과 같습니다.

$$t_s=\frac{4}{\delta\omega_n}=4\tau$$

어디, $\tau$ 시간 상수이고 다음과 같습니다. $\frac{1}{\delta\omega_n}$.

• 두 정착 시간 $t_s$ 및 시간 상수 $\tau$ 감쇠비에 반비례합니다. $\delta$.

• 두 정착 시간 $t_s$ 및 시간 상수 $\tau$시스템 게인과 무관합니다. 즉, 시스템 이득 변경, 안정화 시간$t_s$ 및 시간 상수 $\tau$ 결코 변하지 않을 것입니다.

예

이제 폐 루프 전달 함수가있는 제어 시스템의 시간 도메인 사양을 찾아 보겠습니다. $\frac{4}{s^2+2s+4}$ 단위 스텝 신호가이 제어 시스템에 입력으로 적용될 때.

2 차 폐 루프 제어 시스템의 전달 함수의 표준 형식은 다음과 같습니다.

$$\frac{\omega_n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$

이 두 전달 함수를 동일시하면 감쇠되지 않은 고유 주파수를 얻을 수 있습니다. $\omega_n$ 2rad / sec 및 감쇠비 $\delta$ 0.5로.

감쇠 주파수의 공식을 알고 있습니다. $\omega_d$ 같이

$$\omega_d=\omega_n\sqrt{1-\delta^2}$$

대용품, $\omega_n$ 과 $\delta$ 위 공식의 값.

$$\Rightarrow \omega_d=2\sqrt{1-(0.5)^2}$$

$$\Rightarrow \omega_d=1.732 \: rad/sec$$

대용품, $\delta$ 다음 관계의 가치

$$\theta=\cos^{-1}\delta$$

$$\Rightarrow \theta=\cos^{-1}(0.5)=\frac{\pi}{3}\:rad$$

주어진 전달 함수에 대한 시간 도메인 사양의 값을 얻기 위해 각 시간 도메인 사양의 공식에서 위의 필요한 값을 대체하고 단순화하십시오.

다음 표는 시간 도메인 사양의 공식, 필요한 값의 대체 및 최종 값을 보여줍니다.

시간 도메인 사양	공식	수식의 값 대체	최종 가치
지연 시간	$t_d=\frac{1+0.7\delta}{\omega_n}$	$t_d=\frac{1+0.7(0.5)}{2}$	$t_d$= 0.675 초
상승 시간	$t_r=\frac{\pi-\theta}{\omega_d}$	$t_r=\frac{\pi-(\frac{\pi}{3})}{1.732}$	$t_r$= 1.207 초
피크 타임	$t_p=\frac{\pi}{\omega_d}$	$t_p=\frac{\pi}{1.732}$	$t_p$= 1.813 초
% 피크 오버 슈트	$\%M_p=\left( e^{-\left (\frac{\delta\pi}{\sqrt{1-\delta^2}} \right ) }\right )\times 100\%$	$\%M_p=\left( e^{-\left (\frac{0.5\pi}{\sqrt{1-(0.5)^2}} \right ) }\right )\times 100\%$	$\% \: M_p$= 16.32 %
2 % 공차 대역에 대한 정착 시간	$t_s=\frac{4}{\delta\omega_n}$	$t_S=\frac{4}{(0.5)(2)}$	$t_s$= 4 초

정상 상태 동안 원하는 응답에서 제어 시스템의 출력 편차는 다음과 같이 알려져 있습니다. steady state error. 다음과 같이 표현됩니다.$e_{ss}$. 다음과 같이 최종 값 정리를 사용하여 정상 상태 오류를 찾을 수 있습니다.

$$e_{ss}=\lim_{t \to \infty}e(t)=\lim_{s \to 0}sE(s)$$

어디,

E (s)는 오류 신호의 라플라스 변환입니다. $e(t)$

유니티 피드백 및 비 유니티 피드백 제어 시스템에 대한 정상 상태 오류를 하나씩 찾는 방법에 대해 논의하겠습니다.

Unity 피드백 시스템의 정상 상태 오류

유니티 네거티브 피드백을 갖는 폐쇄 루프 제어 시스템의 다음 블록 다이어그램을 고려하십시오.

어디,

• R (s)는 기준 입력 신호의 라플라스 변환입니다. $r(t)$
• C (s)는 출력 신호의 라플라스 변환입니다. $c(t)$

유니티 네거티브 피드백 폐쇄 루프 제어 시스템의 전달 함수는 다음과 같습니다.

$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$

$$\Rightarrow C(s)=\frac{R(s)G(s)}{1+G(s)}$$

합산 점의 출력은 다음과 같습니다.

$$E(s)=R(s)-C(s)$$

대용품 $C(s)$ 위 방정식의 값.

$$E(s)=R(s)-\frac{R(s)G(s)}{1+G(s)}$$

$$\Rightarrow E(s)=\frac{R(s)+R(s)G(s)-R(s)G(s)}{1+G(s)}$$

$$\Rightarrow E(s)=\frac{R(s)}{1+G(s)}$$

대용품 $E(s)$ 정상 상태 오류 공식의 값

$$e_{ss}=\lim_{s \to 0} \frac{sR(s)}{1+G(s)}$$

다음 표는 단위 단계, 단위 램프 및 단위 포물선 신호와 같은 표준 입력 신호에 대한 정상 상태 오류 및 오류 상수를 보여줍니다.

입력 신호	정상 상태 오류 $e_{ss}$	오류 상수
단위 단계 신호	$\frac{1}{1+k_p}$	$K_p=\lim_{s \to 0}G(s)$
단위 램프 신호	$\frac{1}{K_v}$	$K_v=\lim_{s \to 0}sG(s)$
단위 포물선 신호	$\frac{1}{K_a}$	$K_a=\lim_{s \to 0}s^2G(s)$

어디, $K_p$, $K_v$ 과 $K_a$ 위치 오류 상수, 속도 오류 상수 및 가속 오류 상수입니다.

Note − 위의 입력 신호 중 하나가 단위가 아닌 진폭을 갖는 경우 해당하는 정상 상태 오류를 해당 진폭과 곱하십시오.

Note− 원점에만 존재하기 때문에 단위 임펄스 신호에 대한 정상 상태 오류를 정의 할 수 없습니다. 따라서 임펄스 응답을 단위 임펄스 입력과 비교할 수 없습니다.t 무한대를 나타냅니다.

예

입력 신호에 대한 정상 상태 오류를 찾아 보겠습니다. $r(t)=\left( 5+2t+\frac{t^2}{2} \right )u(t)$ 통합 부정적인 피드백 제어 시스템의 $G(s)=\frac{5(s+4)}{s^2(s+1)(s+20)}$

주어진 입력 신호는 스텝, 램프 및 포물선의 세 가지 신호의 조합입니다. 다음 표는이 세 가지 신호에 대한 오류 상수 및 정상 상태 오류 값을 보여줍니다.

입력 신호	오류 상수	정상 상태 오류
$r_1(t)=5u(t)$	$K_p=\lim_{s \to 0}G(s)=\infty$	$e_{ss1}=\frac{5}{1+k_p}=0$
$r_2(t)=2tu(t)$	$K_v=\lim_{s \to 0}sG(s)=\infty$	$e_{ss2}=\frac{2}{K_v}=0$
$r_3(t)=\frac{t^2}{2}u(t)$	$K_a=\lim_{s \to 0}s^2G(s)=1$	$e_{ss3}=\frac{1}{k_a}=1$

위의 세 가지 정상 상태 오류를 추가하여 전체 정상 상태 오류를 얻습니다.

$$e_{ss}=e_{ss1}+e_{ss2}+e_{ss3}$$

$$\Rightarrow e_{ss}=0+0+1=1$$

따라서 정상 상태 오류가 발생했습니다. $e_{ss}$ 같이 1 이 예에서는.

비 Unity 피드백 시스템에 대한 정상 상태 오류

불일치 네거티브 피드백이있는 폐쇄 루프 제어 시스템의 다음 블록 다이어그램을 고려하십시오.

유니티 피드백 시스템에 대해서만 정상 상태 오류를 찾을 수 있습니다. 그래서 우리는 비-유니티 피드백 시스템을 단일 피드백 시스템으로 변환해야합니다. 이를 위해 위의 블록 다이어그램에 하나의 유니티 포지티브 피드백 경로와 하나의 유니티 네거티브 피드백 경로를 포함하십시오. 새로운 블록 다이어그램은 아래와 같습니다.

유니티 네거티브 피드백을 그대로 유지하여 위의 블록 다이어그램을 단순화하십시오. 다음은 단순화 된 블록 다이어그램입니다.

이 블록 다이어그램은 유니티 네거티브 피드백 폐쇄 루프 제어 시스템의 블록 다이어그램과 유사합니다. 여기서 단일 블록은 전달 기능을 가지고 있습니다.$\frac{G(s)}{1+G(s)H(s)-G(s)}$ 대신에 $G(s)$. 이제 유니티 네거티브 피드백 시스템에 대해 제공된 정상 상태 오류 공식을 사용하여 정상 상태 오류를 계산할 수 있습니다.

Note− 불안정한 폐쇄 루프 시스템에서 정상 상태 오류를 찾는 것은 의미가 없습니다. 따라서 폐쇄 루프 안정 시스템에 대해서만 정상 상태 오류를 계산해야합니다. 즉, 정상 상태 오류를 찾기 전에 제어 시스템이 안정적인지 여부를 확인해야합니다. 다음 장에서는 개념 관련 안정성에 대해 설명합니다.

안정성은 중요한 개념입니다. 이 장에서는 시스템의 안정성과 안정성에 따른 시스템 유형에 대해 설명합니다.

안정성이란 무엇입니까?

출력이 제어되는 경우 시스템은 안정적이라고합니다. 그렇지 않으면 불안정하다고합니다. ㅏstable system 주어진 경계 입력에 대해 경계 출력을 생성합니다.

다음 그림은 안정적인 시스템의 응답을 보여줍니다.

단위 스텝 입력에 대한 1 차 제어 시스템의 응답입니다. 이 응답은 0과 1 사이의 값을 갖습니다. 따라서 제한된 출력입니다. 단위 스텝 신호는 모든 양의 값에 대해 1의 값을가집니다.t0을 포함합니다. 따라서 이것은 제한된 입력입니다. 따라서 1 차 제어 시스템은 입력과 출력이 모두 제한되어 있기 때문에 안정적입니다.

안정성에 기반한 시스템 유형

안정성을 기준으로 시스템을 다음과 같이 분류 할 수 있습니다.

• 절대적으로 안정적인 시스템
• 조건부로 안정적인 시스템
• 한계 적으로 안정적인 시스템

절대적으로 안정적인 시스템

시스템이 모든 범위의 시스템 구성 요소 값에 대해 안정적인 경우 absolutely stable system. 개방 루프 제어 시스템은 개방 루프 전달 함수의 모든 극이 왼쪽 절반에 있으면 절대적으로 안정적입니다.‘s’ plane. 유사하게, 폐쇄 루프 제어 시스템은 폐쇄 루프 전달 함수의 모든 극이 's'평면의 왼쪽 절반에있는 경우 절대적으로 안정적입니다.

조건부로 안정적인 시스템

시스템이 특정 범위의 시스템 구성 요소 값에 대해 안정적이면 다음과 같이 알려져 있습니다. conditionally stable system.

한계 적으로 안정적인 시스템

제한된 입력에 대해 일정한 진폭과 일정한 진동 주파수를 가진 출력 신호를 생성하여 시스템이 안정되면 다음과 같이 알려져 있습니다. marginally stable system. 개방 루프 제어 시스템은 개방 루프 전달 함수의 두 극이 가상 축에 존재하는 경우 약간 안정적입니다. 마찬가지로, 폐 루프 전달 함수의 두 극이 가상 축에 존재하는 경우 폐 루프 제어 시스템은 약간 안정적입니다.

이 장에서는 안정성 분석에 대해 논의하겠습니다. ‘s’RouthHurwitz 안정성 기준을 사용하는 도메인. 이 기준에서는 폐쇄 루프 제어 시스템의 안정성을 찾기 위해 특성 방정식이 필요합니다.

Routh-Hurwitz 안정성 기준

Routh-Hurwitz 안정성 기준에는 하나의 필수 조건과 안정성을위한 충분한 조건이 있습니다. 제어 시스템이 필요한 조건을 충족하지 않으면 제어 시스템이 불안정하다고 말할 수 있습니다. 그러나 제어 시스템이 필요한 조건을 충족하면 안정적 일 수도 있고 아닐 수도 있습니다. 따라서 충분한 조건은 제어 시스템이 안정적인지 여부를 파악하는 데 도움이됩니다.

Routh-Hurwitz 안정성에 필요한 조건

필요한 조건은 특성 다항식의 계수가 양수 여야한다는 것입니다. 이것은 특성 방정식의 모든 근이 음의 실수 부분을 가져야 함을 의미합니다.

주문 'n'의 특성 방정식을 고려하십시오.

$$a_0s^n+a_1s^{n-1}+a_2s^{n-2}+...+a_{n-1}s^1+a_ns^0=0$$

여기에 누락 된 용어가 없어야합니다. n^th주문 특성 방정식. 이것은n^th 차수 특성 방정식은 값이 0 인 계수를 가져서는 안됩니다.

Routh-Hurwitz 안정성을위한 충분한 조건

충분한 조건은 Routh 배열의 첫 번째 열에있는 모든 요소가 동일한 부호를 가져야한다는 것입니다. 이는 Routh 배열의 첫 번째 열에있는 모든 요소가 양수 또는 음수 여야 함을 의미합니다.

Routh 배열 방법

특성 방정식의 모든 근이 's'평면의 왼쪽 절반에 존재하면 제어 시스템이 안정적입니다. 's'평면의 오른쪽 절반에 특성 방정식의 근이 하나 이상 있으면 제어 시스템이 불안정합니다. 따라서 제어 시스템이 안정적인지 불안정한 지 알기 위해 특성 방정식의 근을 찾아야합니다. 그러나 차수가 증가함에 따라 특성 방정식의 근본을 찾기는 어렵다.

그래서,이 문제를 극복하기 위해 우리는 Routh array method. 이 방법에서는 특성 방정식의 근을 계산할 필요가 없습니다. 먼저 Routh 테이블을 공식화하고 Routh 테이블의 첫 번째 열에서 부호 변경 번호를 찾습니다. Routh 테이블의 첫 번째 열에있는 부호 변경 횟수는 's'평면의 오른쪽 절반에 존재하는 특성 방정식의 근 수를 제공하며 제어 시스템이 불안정합니다.

Routh 테이블을 구성하려면이 절차를 따르십시오.

• Routh 배열의 처음 두 행을 아래 표에 언급 된 특성 다항식의 계수로 채 웁니다. 계수로 시작$s^n$ 그리고 계수까지 계속 $s^0$.

• Routh 배열의 나머지 행을 아래 표에 언급 된 요소로 채 웁니다. 첫 번째 열 요소를 얻을 때까지이 프로세스를 계속하십시오.row $s^0$ 이다 $a_n$. 여기,$a_n$ 계수입니다 $s^0$ 특성 다항식에서.

Note − Routh 테이블의 행 요소에 공통 요소가있는 경우 단순화를 위해 해당 요소로 행 요소를 나눌 수 있습니다.

다음 표에 나타낸다 (N)의 배열 Routh 보통 ^번째 오더 특성 다항식.

$$a_0s^n+a_1s^{n-1}+a_2s^{n-2}+...+a_{n-1}s^1+a_ns^0$$

$s^n$	$a_0$	$a_2$	$a_4$	$a_6$	...	...
$s^{n-1}$	$a_1$	$a_3$	$a_5$	$a_7$	...	...
$s^{n-2}$	$b_1=\frac{a_1a_2-a_3a_0}{a_1}$	$b_2=\frac{a_1a_4-a_5a_0}{a_1}$	$b_3=\frac{a_1a_6-a_7a_0}{a_1}$	...	...	...
$s^{n-3}$	$c_1=\frac{b_1a_3-b_2a_1}{b_1}$	$c_2=\frac{b_1a_55-b_3a_1}{b_1}$	$\vdots$
$\vdots $	$\vdots$	$\vdots$	$\vdots$
$s^1$	$\vdots$	$\vdots$
$s^0$	$a_n$

Example

특성 방정식을 갖는 제어 시스템의 안정성을 찾아 보자.

$$s^4+3s^3+3s^2+2s+1=0$$

Step 1 − Routh-Hurwitz 안정성에 필요한 조건을 확인합니다.

특성 다항식의 모든 계수, $s^4+3s^3+3s^2+2s+1$긍정적입니다. 따라서 제어 시스템은 필요한 조건을 충족합니다.

Step 2 − 주어진 특성 다항식에 대한 Routh 배열을 형성합니다.

$s^4$	$1$	$3$	$1$
$s^3$	$3$	$2$
$s^2$	$\frac{(3 \times 3)-(2 \times 1)}{3}=\frac{7}{3}$	$\frac{(3 \times 1)-(0 \times 1)}{3}=\frac{3}{3}=1$
$s^1$	$\frac{\left ( \frac{7}{3}\times 2 \right )-(1 \times 3)}{\frac{7}{3}}=\frac{5}{7}$
$s^0$	$1$

Step 3 − Routh-Hurwitz 안정성을위한 충분한 조건을 확인합니다.

Routh 배열의 첫 번째 열에있는 모든 요소는 양수입니다. Routh 배열의 첫 번째 열에는 부호 변경이 없습니다. 따라서 제어 시스템은 안정적입니다.

Routh Array의 특수 사례

Routh 테이블을 구성하는 동안 두 가지 유형의 상황이 발생할 수 있습니다. 이 두 상황에서 Routh 테이블을 완성하는 것은 어렵습니다.

두 가지 특별한 경우는-

• Routh 배열 행의 첫 번째 요소는 0입니다.
• Routh 배열 행의 모든 ​​요소는 0입니다.

이제이 두 경우의 어려움을 하나씩 하나씩 극복하는 방법을 논의하겠습니다.

Routh 배열 행의 첫 번째 요소가 0입니다.

Routh 배열의 행에 첫 번째 요소 만 0으로 포함되고 나머지 요소 중 하나 이상의 값이 0이 아닌 경우 첫 번째 요소를 작은 양의 정수로 바꿉니다. $\epsilon$. 그런 다음 Routh 테이블을 완료하는 프로세스를 계속하십시오. 이제 다음을 대체하여 Routh 테이블의 첫 번째 열에서 부호 변경 수를 찾으십시오.$\epsilon$ 0이되는 경향이 있습니다.

Example

특성 방정식을 갖는 제어 시스템의 안정성을 찾아 보자.

$$s^4+2s^3+s^2+2s+1=0$$

Step 1 − Routh-Hurwitz 안정성에 필요한 조건을 확인합니다.

특성 다항식의 모든 계수, $s^4+2s^3+s^2+2s+1$긍정적입니다. 따라서 제어 시스템은 필요한 조건을 충족했습니다.

Step 2 − 주어진 특성 다항식에 대한 Routh 배열을 형성합니다.

$s^4$	$1$	$1$	$1$
$s^3$	2 1	2 1
$s^2$	$\frac{(1 \times 1)-(1 \times 1)}{1}=0$	$\frac{(1 \times 1)-(0 \times 1)}{1}=1$
$s^1$
$s^0$

행 $s^3$요소는 공약수로 2를 갖습니다. 따라서 이러한 모든 요소는 2로 나뉩니다.

Special case (i) − 행의 첫 번째 요소 만 $s^2$0입니다. 따라서 다음으로 교체하십시오.$\epsilon$ Routh 테이블을 완료하는 과정을 계속합니다.

$s^4$	1	1	1
$s^3$	1	1
$s^2$	$\epsilon$	1
$s^1$	$\frac{\left ( \epsilon \times 1 \right )-\left ( 1 \times 1 \right )}{\epsilon}=\frac{\epsilon-1}{\epsilon}$
$s^0$	1

Step 3 − Routh-Hurwitz 안정성을위한 충분한 조건을 확인합니다.

같이 $\epsilon$ 0이되는 경우 Routh 테이블은 다음과 같이됩니다.

$s^4$	1	1	1
$s^3$	1	1
$s^2$	0	1
$s^1$	-∞
$s^0$	1

Routh 테이블의 첫 번째 열에 두 개의 기호 변경이 있습니다. 따라서 제어 시스템이 불안정합니다.

Routh 배열 행의 모든 ​​요소는 0입니다.

이 경우 다음 두 단계를 따르십시오.

• 0으로 이루어진 행 바로 위에있는 행의 보조 방정식 A (s)를 작성합니다.

• s에 대해 보조 방정식 A (s)를 미분합니다. 이 계수로 0 행을 채 웁니다.

Example

특성 방정식을 갖는 제어 시스템의 안정성을 찾아 보자.

$$s^5+3s^4+s^3+3s^2+s+3=0$$

Step 1 − Routh-Hurwitz 안정성에 필요한 조건을 확인합니다.

주어진 특성 다항식의 모든 계수는 양수입니다. 따라서 제어 시스템은 필요한 조건을 충족했습니다.

Step 2 − 주어진 특성 다항식에 대한 Routh 배열을 형성합니다.

$s^5$	1	1	1
$s^4$	3 1	3 1	3 1
$s^3$	$\frac{(1 \times 1)-(1 \times 1)}{1}=0$	$\frac{(1 \times 1)-(1 \times 1)}{1}=0$
$s^2$
$s^1$
$s^0$

행 $s^4$ 요소의 공약수는 3입니다. 따라서이 모든 요소는 3으로 나뉩니다.

Special case (ii) − 행의 모든 ​​요소 $s^3$0입니다. 그래서, 행의 보조 방정식 A (s)를 쓰십시오$s^4$.

$$A(s)=s^4+s^2+1$$

s에 대해 위의 방정식을 미분하십시오.

$$\frac{\text{d}A(s)}{\text{d}s}=4s^3+2s$$

이 계수를 행에 배치 $s^3$.

$s^5$	1	1	1
$s^4$	1	1	1
$s^3$	4 2	2 1
$s^2$	$\frac{(2 \times 1)-(1 \times 1)}{2}=0.5$	$\frac{(2 \times 1)-(0 \times 1)}{2}=1$
$s^1$	$\frac{(0.5 \times 1)-(1 \times 2)}{0.5}=\frac{-1.5}{0.5}=-3$
$s^0$	1

Step 3 − Routh-Hurwitz 안정성을위한 충분한 조건을 확인합니다.

Routh 테이블의 첫 번째 열에 두 개의 기호 변경이 있습니다. 따라서 제어 시스템이 불안정합니다.

Routh-Hurwitz 안정성 기준에서 닫힌 루프 극이 's'평면의 왼쪽 절반에 있는지 아니면 's'평면의 오른쪽 절반에 있는지 또는 가상 축에 있는지 알 수 있습니다. 그래서 우리는 제어 시스템의 본질을 찾을 수 없습니다. 이 한계를 극복하기 위해 루트 궤적이라는 기술이 있습니다. 이 기술은 다음 두 장에서 논의 할 것입니다.

근 궤적 다이어그램에서 폐쇄 루프 극의 경로를 관찰 할 수 있습니다. 따라서 제어 시스템의 특성을 확인할 수 있습니다. 이 기술에서는 개방 루프 전달 함수를 사용하여 폐쇄 루프 제어 시스템의 안정성을 알 수 있습니다.

Root Locus의 기초

루트 궤적은 시스템 게인 K를 0에서 무한대로 변경하여 특성 방정식의 루트 궤적입니다.

폐 루프 제어 시스템의 특성 방정식은

$$1+G(s)H(s)=0$$

우리는 대표 할 수 있습니다 $G(s)H(s)$ 같이

$$G(s)H(s)=K\frac{N(s)}{D(s)}$$

어디,

• K는 곱셈 계수를 나타냅니다.

• N (S)를 갖는 분자 용어 (반영) n은 ^제 'S'의 차 다항식.

• D (S)를 갖는 분 모항 (반영)에요 나타낸다 ^번째 'S'의 차 다항식.

대용품, $G(s)H(s)$ 특성 방정식의 값.

$$1+k\frac{N(s)}{D(s)}=0$$

$$\Rightarrow D(s)+KN(s)=0$$

Case 1 − K = 0

만약 $K=0$, 다음 $D(s)=0$.

즉, K가 0 일 때 폐쇄 루프 극은 개방 루프 극과 동일합니다.

Case 2 − K = ∞

위의 특성 방정식을 다음과 같이 다시 작성하십시오.

$$K\left(\frac{1}{K}+\frac{N(s)}{D(s)} \right )=0 \Rightarrow \frac{1}{K}+\frac{N(s)}{D(s)}=0$$

대용품, $K = \infty$ 위의 방정식에서.

$$\frac{1}{\infty}+\frac{N(s)}{D(s)}=0 \Rightarrow \frac{N(s)}{D(s)}=0 \Rightarrow N(s)=0$$

만약 $K=\infty$, 다음 $N(s)=0$. 이는 K가 무한대 일 때 폐쇄 루프 극이 개방 루프 0과 동일 함을 의미합니다.

위의 두 가지 경우에서 루트 궤적 분기는 개방 루프 극에서 시작하고 개방 루프 0에서 끝나는 것으로 결론을 내릴 수 있습니다.

각도 조건 및 크기 조건

루트 궤적 가지의 점은 각도 조건을 충족합니다. 따라서 각도 조건은 점이 루트 궤적 가지에 존재하는지 여부를 알 때 사용됩니다. 크기 조건을 사용하여 루트 궤적 가지의 점에 대한 K 값을 찾을 수 있습니다. 따라서 점에 대한 크기 조건을 사용할 수 있으며 이는 각도 조건을 충족합니다.

폐 루프 제어 시스템의 특성 방정식은 다음과 같습니다.

$$1+G(s)H(s)=0$$

$$\Rightarrow G(s)H(s)=-1+j0$$

그만큼 phase angle 의 $G(s)H(s)$ 이다

$$\angle G(s)H(s)=\tan^{-1}\left ( \frac{0}{-1} \right )=(2n+1)\pi$$

그만큼 angle condition개 루프 전달 함수의 각도가 180 ⁰ 의 홀수 배수 인 지점 입니다.

규모 $G(s)H(s)$ -

$$|G(s)H(s)|=\sqrt {(-1)^2+0^2}=1$$

크기 조건은 개방 루프 전달 함수의 크기가 1 인 지점 (각도 조건을 충족)입니다.

그만큼 root locuss 도메인의 그래픽 표현이며 실제 축에 대해 대칭입니다. 개방 루프 극점과 0이 실수 또는 복합 켤레 쌍으로 값을 갖는 s 도메인에 존재하기 때문입니다. 이 장에서는 루트 궤적을 구성 (그리기)하는 방법에 대해 설명합니다.

루트 궤적 생성 규칙

루트 궤적을 구성하려면 다음 규칙을 따르십시오.

Rule 1 − 's'평면에서 개방 루프 극점과 영점을 찾습니다.

Rule 2 − 근 궤적 가지의 수를 찾으십시오.

루트 궤적 분기는 개방 루프 극에서 시작하고 개방 루프 0에서 끝납니다. 그래서 뿌리 궤적 가지의 수는N 유한 개방 루프 극의 수와 같습니다. P 또는 유한 개방 루프 제로의 수 Z, 어느 쪽이 더 큰지.

수학적으로 근 궤적 가지의 수를 쓸 수 있습니다. N 같이

$N=P$ 만약 $P\geq Z$

$N=Z$ 만약 $P<Z$

Rule 3 − 식별하고 그립니다 real axis root locus branches.

한 점에서 개 루프 전달 함수의 각도가 180 ⁰ 의 홀수 배수 이면 해당 점은 근 궤적에 있습니다. 실제 축에있는 점의 왼쪽에 홀수 개의 개방 루프 극과 0이 존재하는 경우 해당 점은 루트 궤적 분기에 있습니다. 따라서이 조건을 만족하는 지점의 분기가 근 궤적 분기의 실제 축입니다.

Rule 4 − 점근선의 중심과 각도를 구합니다.

• 만약 $P = Z$, 모든 루트 궤적 분기는 유한 개방 루프 극에서 시작하여 유한 개방 루프 0에서 끝납니다.

• 만약 $P > Z$ , 다음 $Z$ 루트 궤적 분기의 수는 유한 개방 루프 극에서 시작하여 유한 개방 루프 0에서 끝납니다. $P − Z$ 루트 궤적 분기의 수는 유한 개방 루프 극에서 시작하여 무한 개방 루프 0에서 끝납니다.

• 만약 $P < Z$ , 그러면 P 개의 루트 궤적 분기가 유한 개방 루프 극에서 시작하여 유한 개방 루프 0에서 끝납니다. $Z − P$ 루트 궤적 분기의 수는 무한 개방 루프 극에서 시작하여 유한 개방 루프 0에서 끝납니다.

따라서 일부 루트 궤적 분기는 무한대에 접근합니다. $P \neq Z$. 점근선은 이러한 뿌리 궤적 가지의 방향을 제공합니다. 실제 축에서 점근선의 교차점은 다음과 같이 알려져 있습니다.centroid.

우리는 계산할 수 있습니다 centroid α 이 공식을 사용하여

$\alpha = \frac{\sum Real\: part\: of\: finite\: open\: loop\: poles\:-\sum Real\: part\: of\: finite\: open\: loop\: zeros}{P-Z}$

각도에 대한 공식 asymptotes θ 이다

$$\theta=\frac{(2q+1)180^0}{P-Z}$$

어디,

$$q=0,1,2,....,(P-Z)-1$$

Rule 5 − 가상 축을 사용하여 루트 궤적 가지의 교차점을 찾습니다.

루트 궤적 가지가 가상 축과 교차하는 지점을 계산할 수 있습니다. K 그 시점에서 Routh 배열 방법과 특수 case (ii).

• Routh 배열 행의 모든 ​​요소가 0이면 루트 궤적 분기가 가상 축과 교차하고 그 반대의 경우도 마찬가지입니다.

• 첫 번째 요소를 0으로 만들면 전체 행의 요소가 0이되는 방식으로 행을 식별합니다. 가치 찾기K 이 조합을 위해.

• 이것을 대체하십시오 K보조 방정식의 값. 가상 축과 루트 궤적 분기의 교차점을 얻습니다.

Rule 6 − 이탈 및 이탈 지점을 찾습니다.

• 두 개의 열린 루프 극 사이에 실제 축 루트 궤적 분기가 있으면 break-away point 이 두 개의 개방 루프 기둥 사이에 있습니다.

• 두 개의 개방 루프 제로 사이에 실제 축 루트 궤적 분기가 있으면 break-in point 이 두 개의 개방 루프 제로 사이에 있습니다.

Note − 이탈 및 이탈 지점은 실제 축 루트 궤적 분기에만 존재합니다.

다음 단계에 따라 이탈 및 이탈 지점을 찾으십시오.

• 쓰다 $K$ 측면에서 $s$ 특성 방정식에서 $1 + G(s)H(s) = 0$.

• 구별 짓다 $K$s와 관련하여 0이되도록합니다. 이 값을$s$ 위의 방정식에서.

• 가치 $s$ 어떤 $K$ 값은 양수입니다 break points.

Rule 7 − 출발 각도와 도착 각도를 찾으십시오.

출발 각도와 도착 각도는 각각 복합 켤레 개방 루프 극점과 복합 켤레 개방 루프 0에서 계산할 수 있습니다.

에 대한 공식 angle of departure $\phi_d$ 이다

$$\phi_d=180^0-\phi$$

에 대한 공식 angle of arrival $\phi_a$ 이다

$$\phi_a=180^0+\phi$$

어디,

$$\phi=\sum \phi_P-\sum \phi_Z$$

예

이제 개방 루프 전달 함수를 갖는 제어 시스템의 루트 궤적을 그리겠습니다. $G(s)H(s)=\frac{K}{s(s+1)(s+5)}$

Step 1 − 주어진 개 루프 전달 함수는 $s = 0, s = −1$ 과 $s = −5$. 0이 없습니다. 따라서 루트 궤적 분기의 수는 개방 루프 전달 함수의 극 수와 같습니다.

$$N=P=3$$

세 개의 극이 위 그림에 나와 있습니다. 사이의 선분$s = −1$ 과 $s = 0$실제 축에서 루트 궤적의 한 가지입니다. 그리고 실제 축에있는 루트 궤적의 다른 가지는 왼쪽에있는 선분입니다.$s = −5$.

Step 2 − 주어진 공식을 사용하여 중심의 값과 점근선의 각도를 얻습니다.

중심 $\alpha = −2$

점근선의 각도는 다음과 같습니다. $\theta = 60^0,180^0$ 과 $300^0$.

다음 그림은 중심과 3 개의 점근선을 보여줍니다.

Step 3 − 두 점근선은 각이 $60^0$ 과 $300^0$, 두 개의 루트 궤적 가지가 가상 축과 교차합니다. Routh 배열 방법과 특수한 경우 (ii)를 사용하면 루트 궤적 가지가 가상 축과 교차합니다.$j\sqrt{5}$ 과 $−j\sqrt{5}$.

극 사이의 실제 축 루트 궤적 분기에 하나의 이탈 지점이 있습니다. $s = −1$ 과 $s = 0$. 이탈 점 계산에 주어진 절차를 따르면 다음과 같이 얻을 수 있습니다.$s = −0.473$.

주어진 제어 시스템에 대한 루트 궤적 다이어그램은 다음 그림에 나와 있습니다.

이러한 방식으로 모든 제어 시스템의 근 궤적 다이어그램을 그리고 폐쇄 루프 전달 함수의 극 이동을 관찰 할 수 있습니다.

근 궤적 다이어그램에서 다양한 감쇠 유형에 대한 K 값의 범위를 알 수 있습니다.

루트 궤적에 개방 루프 극점 및 영점 추가의 효과

루트 궤적은 ‘s’ plane 개방 루프 극과 개방 루프 0을 추가하여

• 개방 루프 전달 함수에 극을 포함하면 루트 궤적 분기 중 일부가 's'평면의 오른쪽 절반으로 이동합니다. 이 때문에 감쇠비는$\delta$감소합니다. 즉, 감쇠 된 주파수$\omega_d$ 증가하고 지연 시간과 같은 시간 도메인 사양 $t_d$, 상승 시간 $t_r$ 및 피크 타임 $t_p$감소. 그러나 시스템 안정성에 영향을 미칩니다.

• 개방 루프 전달 함수에 0을 포함하면 루트 궤적 분기 중 일부가 's'평면의 왼쪽 절반으로 이동합니다. 따라서 제어 시스템 안정성이 향상됩니다. 이 경우 감쇠비$\delta$증가합니다. 즉, 감쇠 된 주파수$\omega_d$ 감소 및 지연 시간과 같은 시간 도메인 사양 $t_d$, 상승 시간 $t_r$ 및 피크 타임 $t_p$ 증가하다.

따라서 요구 사항에 따라 전달 함수에 개방 루프 극점 또는 0을 포함 (추가) 할 수 있습니다.

우리는 이미 제어 시스템의 시간 응답 분석과 2 차 제어 시스템의 시간 도메인 사양에 대해 논의했습니다. 이 장에서는 제어 시스템의 주파수 응답 분석과 2 차 제어 시스템의 주파수 도메인 사양에 대해 설명합니다.

주파수 응답이란 무엇입니까?

시스템의 응답은 과도 응답과 정상 상태 응답으로 나눌 수 있습니다. 푸리에 적분을 사용하여 과도 응답을 찾을 수 있습니다. 입력 정현파 신호에 대한 시스템의 정상 상태 응답은frequency response. 이 장에서는 정상 상태 응답에만 초점을 맞출 것입니다.

정현파 신호가 LTI (Linear Time-Invariant) 시스템에 입력으로 적용되면 정현파 신호 인 정상 상태 출력이 생성됩니다. 입력 및 출력 정현파 신호의 주파수는 동일하지만 진폭과 위상 각도는 다릅니다.

입력 신호를-

$$r(t)=A\sin(\omega_0t)$$

개방 루프 전달 함수는 다음과 같습니다.

$$G(s)=G(j\omega)$$

우리는 대표 할 수 있습니다 $G(j\omega)$ 아래와 같이 크기 및 위상 측면에서.

$$G(j\omega)=|G(j\omega)| \angle G(j\omega)$$

대용품, $\omega = \omega_0$ 위의 방정식에서.

$$G(j\omega_0)=|G(j\omega_0)| \angle G(j\omega_0)$$

출력 신호는

$$c(t)=A|G(j\omega_0)|\sin(\omega_0t + \angle G(j\omega_0))$$

• 그만큼 amplitude 출력 정현파 신호의 크기는 입력 정현파 신호의 진폭과 크기를 곱하여 구합니다. $G(j\omega)$ ...에서 $\omega = \omega_0$.

• 그만큼 phase 출력 정현파 신호의 위상은 입력 정현파 신호의 위상과 $G(j\omega)$ ...에서 $\omega = \omega_0$.

어디,

• A 입력 정현파 신호의 진폭입니다.

• ω₀ 입력 정현파 신호의 각 주파수입니다.

우리는 각 주파수를 쓸 수 있습니다 $\omega_0$ 아래 그림과 같이.

$$\omega_0=2\pi f_0$$

여기, $f_0$입력 정현파 신호의 주파수입니다. 마찬가지로 폐쇄 루프 제어 시스템에 대해서도 동일한 절차를 따를 수 있습니다.

주파수 도메인 사양

주파수 도메인 사양은 다음과 같습니다. resonant peak, resonant frequency and bandwidth.

2 차 폐 루프 제어 시스템의 전달 함수를 다음과 같이 고려하십시오.

$$T(s)=\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$

대용품, $s = j\omega$ 위의 방정식에서.

$$T(j\omega)=\frac{\omega_n^2}{(j\omega)^2+2\delta\omega_n(j\omega)+\omega_n^2}$$

$$\Rightarrow T(j\omega)=\frac{\omega_n^2}{-\omega^2+2j\delta\omega\omega_n+\omega_n^2}=\frac{\omega_n^2}{\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )}$$

$$\Rightarrow T(j\omega)=\frac{1}{\left ( 1-\frac{\omega^2}{\omega_n^2} \right )+j\left ( \frac{2\delta\omega}{\omega_n} \right )}$$

허락하다, $\frac{\omega}{\omega_n}=u$ 위의 방정식에서이 값을 대체하십시오.

$$T(j\omega)=\frac{1}{(1-u^2)+j(2\delta u)}$$

규모 $T(j\omega)$ -

$$M=|T(j\omega)|=\frac{1}{\sqrt {(1-u^2)^2+(2\delta u)^2}}$$

단계 $T(j\omega)$ -

$$\angle T(j\omega)=-tan^{-1}\left( \frac{2\delta u}{1-u^2} \right )$$

공진 주파수

주파수 응답의 크기가 처음으로 피크 값을 갖는 주파수입니다. 다음과 같이 표시됩니다.$\omega_r$. 에서$\omega = \omega_r$, 크기의 첫 번째 도함수 $T(j\omega)$ 0입니다.

구별 짓다 $M$ 에 관하여 $u$.

$$\frac{\text{d}M}{\text{d}u}=-\frac{1}{2}\left [ (1-u^2)^2+(2\delta u)^2 \right ]^{\frac{-3}{2}} \left [2(1-u^2)(-2u)+2(2\delta u)(2\delta) \right ]$$

$$\Rightarrow \frac{\text{d}M}{\text{d}u}=-\frac{1}{2}\left [ (1-u^2)^2+(2\delta u)^2 \right ]^{\frac{-3}{2}} \left [4u(u^2-1 +2\delta^2) \right ]$$

대용품, $u=u_r$ 과 $\frac{\text{d}M}{\text{d}u}==0$ 위의 방정식에서.

$$0=-\frac{1}{2}\left [ (1-u_r^2)^2+(2\delta u_r)^2 \right ]^{-\frac{3}{2}}\left [ 4u_r(u_r^2-1 +2\delta^2) \right ]$$

$$\Rightarrow 4u_r(u_r^2-1 +2\delta^2)=0$$

$$\Rightarrow u_r^2-1+2\delta^2=0$$

$$\Rightarrow u_r^2=1-2\delta^2$$

$$\Rightarrow u_r=\sqrt{1-2\delta^2}$$

대용품, $u_r=\frac{\omega_r}{\omega_n}$ 위의 방정식에서.

$$\frac{\omega_r}{\omega_n}=\sqrt{1-2\delta^2}$$

$$\Rightarrow \omega_r=\omega_n \sqrt{1-2\delta^2}$$

공명 피크

크기의 피크 (최대) 값입니다. $T(j\omega)$. 다음과 같이 표시됩니다.$M_r$.

에서 $u = u_r$, 크기 $T(j\omega)$ -

$$M_r=\frac{1}{\sqrt{(1-u_r^2)^2+(2\delta u_r)^2}}$$

대용품, $u_r = \sqrt{1 − 2\delta^2}$ 과 $1 − u_r^2 = 2\delta^2$ 위의 방정식에서.

$$M_r=\frac{1}{\sqrt{(2\delta^2)^2+(2\delta \sqrt{1-2\delta^2})^2}}$$

$$\Rightarrow M_r=\frac{1}{2\delta \sqrt {1-\delta^2}}$$

주파수 응답의 공진 피크는 특정 감쇠비 값에 대한 시간 도메인 과도 응답의 피크 오버 슈트에 해당합니다. $\delta$. 따라서 공진 피크와 피크 오버 슈트는 서로 상관됩니다.

대역폭

그것은 주파수의 범위입니다. $T(j\omega)$ 제로 주파수 값에서 70.7 %로 떨어집니다.

에서 $\omega = 0$, 의 가치 $u$ 0이됩니다.

대용품, $u = 0$ M.

$$M=\frac{1}{\sqrt {(1-0^2)^2+(2\delta(0))^2}}=1$$

따라서 $T(j\omega)$ 에 하나입니다 $\omega = 0$.

3dB 주파수에서 $T(j\omega)$ 규모의 70.7 %가 될 것입니다. $T(j\omega)$ ...에서 $\omega = 0$.

즉, $\omega = \omega_B, M = 0.707(1) = \frac{1}{\sqrt{2}}$

$$\Rightarrow M=\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{(1-u_b^2)^2+(2\delta u_b)^2}}$$

$$\Rightarrow 2=(1-u_b^2)^2+(2\delta)^2 u_b^2$$

허락하다, $u_b^2=x$

$$\Rightarrow 2=(1-x)^2+(2\delta)^2 x$$

$$\Rightarrow x^2+(4\delta^2-2)x-1=0$$

$$\Rightarrow x=\frac{-(4\delta^2 -2)\pm \sqrt{(4\delta^2-2)^2+4}}{2}$$

x의 양수 값만 고려하십시오.

$$x=1-2\delta^2+\sqrt {(2\delta^2-1)^2+1}$$

$$\Rightarrow x=1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}$$

대용품, $x=u_b^2=\frac{\omega_b^2}{\omega_n^2}$

$$\frac{\omega_b^2}{\omega_n^2}=1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}$$

$$\Rightarrow \omega_b=\omega_n \sqrt {1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}}$$

대역폭 $\omega_b$ 주파수 응답에서 상승 시간에 반비례합니다. $t_r$ 시간 영역 과도 응답에서.

Bode 플롯 또는 Bode 다이어그램은 두 개의 플롯으로 구성됩니다.

• 크기 플롯
• 위상 플롯

두 플롯 모두에서 x 축은 각 주파수 (로그 스케일)를 나타냅니다. 반면에 y 축은 크기 플롯에서 개방 루프 전달 함수의 크기 (선형 스케일)와 위상 플롯에서 개방 루프 전달 함수의 위상 각 (선형 스케일)을 나타냅니다.

그만큼 magnitude 개방 루프 전달 함수의 dB는-

$$M=20\: \log|G(j\omega)H(j\omega)|$$

그만큼 phase angle 개방 루프 전달 함수의 각도는-

$$\phi=\angle G(j\omega)H(j\omega)$$

Note − 로그의 밑은 10입니다.

보드 플롯의 기본

다음 표는 개방 루프 전달 함수에있는 항의 기울기, 크기 및 위상 각 값을 보여줍니다. 이 데이터는 보드 플롯을 그리는 동안 유용합니다.

용어 유형	G (jω) H (jω)	기울기 (dB / dec)	크기 (dB)	위상 각 (도)
일정한	$K$	$0$	$20 \log K$	$0$
원점에서 0	$j\omega$	$20$	$20 \log \omega$	$90$
원점에서 'n'0	$(j\omega)^n$	$20\: n$	$20\: n \log \omega$	$90\: n$
원점의 극	$\frac{1}{j\omega}$	$-20$	$-20 \log \omega$	$-90 \: or \: 270$
원점의 'n'극	$\frac{1}{(j\omega)^n}$	$-20\: n$	$-20 \: n \log \omega$	$-90 \: n \: or \: 270 \: n$
단순 제로	$1+j\omega r$	$20$	$0\: for\: \omega < \frac{1}{r}$ $20\: \log \omega r\: for \: \omega > \frac{1}{r}$	$0 \: for \: \omega < \frac{1}{r}$ $90 \: for \: \omega > \frac{1}{r}$
단순 극	$\frac{1}{1+j\omega r}$	$-20$	$0\: for\: \omega < \frac{1}{r}$ $-20\: \log \omega r\: for\: \omega > \frac{1}{r}$	$0 \: for \: \omega < \frac{1}{r}$ $-90\: or \: 270 \: for\: \omega > \frac{1}{r}$
2 차 미분 항	$\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )$	$40$	$40\: \log\: \omega_n\: for \: \omega < \omega_n$ $20\: \log\:(2\delta\omega_n^2)\: for \: \omega=\omega_n$ $40 \: \log \: \omega\:for \:\omega > \omega_n$	$0 \: for \: \omega < \omega_n$ $90 \: for \: \omega = \omega_n$ $180 \: for \: \omega > \omega_n$
2 차 적분 항	$\frac{1}{\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )}$	$-40$	$-40\: \log\: \omega_n\: for \: \omega < \omega_n$ $-20\: \log\:(2\delta\omega_n^2)\: for \: \omega=\omega_n$ $-40 \: \log \: \omega\:for \:\omega > \omega_n$	$-0 \: for \: \omega < \omega_n$ $-90 \: for \: \omega = \omega_n$ $-180 \: for \: \omega > \omega_n$

개방 루프 전달 함수를 고려하십시오. $G(s)H(s) = K$.

크기 $M = 20\: \log K$ dB

위상 각도 $\phi = 0$ 도

만약 $K = 1$이면 크기는 0dB입니다.

만약 $K > 1$이면 크기는 양수입니다.

만약 $K < 1$이면 크기는 음수가됩니다.

다음 그림은 해당 보드 플롯을 보여줍니다.

크기 플롯은 주파수와 무관 한 수평선입니다. 0dB 라인 자체는 K 값이 1 일 때 크기 플롯입니다. K의 양수 값의 경우 수평선이 이동합니다.$20 \:\log K$0dB 라인 위의 dB. K의 음수 값의 경우 수평선이 이동합니다.$20\: \log K$0dB 라인 아래의 dB. 0도 선 자체는 K의 모든 양수 값에 대한 위상 플롯입니다.

개방 루프 전달 함수를 고려하십시오. $G(s)H(s) = s$.

크기 $M = 20 \log \omega$ dB

위상 각도 $\phi = 90^0$

에서 $\omega = 0.1$ rad / sec, 크기는 -20dB입니다.

에서 $\omega = 1$ rad / sec, 크기는 0dB입니다.

에서 $\omega = 10$ rad / sec, 크기는 20dB입니다.

다음 그림은 해당 보드 플롯을 보여줍니다.

크기 플롯은 20dB / dec의 기울기를 갖는 선입니다. 이 라인은$\omega = 0.1$rad / sec의 크기는 -20dB이며 동일한 기울기에서 계속됩니다. 0dB 라인을 터치하고 있습니다.$\omega = 1$rad / 초 이 경우 위상 플롯은 90 ⁰ 라인입니다.

개방 루프 전달 함수를 고려하십시오. $G(s)H(s) = 1 + s\tau$.

크기 $M = 20\: log \sqrt{1 + \omega^2\tau^2}$ dB

위상 각도 $\phi = \tan^{-1}\omega\tau$ 도

에 대한 $ω < \frac{1}{\tau}$ , 크기는 0dB이고 위상 각은 0 도입니다.

에 대한 $\omega > \frac{1}{\tau}$ , 크기는 $20\: \log \omega\tau$dB 및 위상 각은 90 ⁰ 입니다.

다음 그림은 해당 보드 플롯을 보여줍니다.

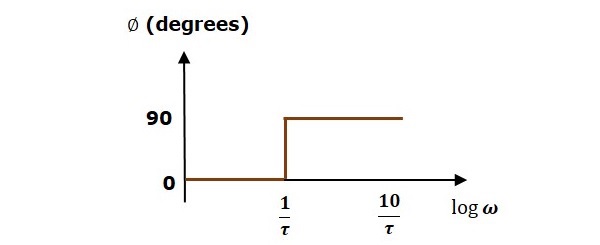
크기 플롯의 크기는 0dB입니다. $\omega=\frac{1}{\tau}$rad / 초 에서$\omega = \frac{1}{\tau}$rad / sec, 20dB / dec의 기울기를가집니다. 이 경우 위상 플롯은 최대 0 도의 위상 각을 갖습니다.$\omega = \frac{1}{\tau}$rad / sec이고 여기서부터는 90 ^0의 위상 각을 갖습니다 . 이 Bode 플롯은asymptotic Bode plot.

크기 및 위상 플롯이 직선으로 표시되므로 Exact Bode 플롯은 점근 적 보드 플롯과 유사합니다. 유일한 차이점은 Exact Bode 플롯에는 직선 대신 단순한 곡선이 있다는 것입니다.

유사하게, 테이블에 주어진 개방 루프 전달 함수의 다른 항에 대한 Bode 플롯을 그릴 수 있습니다.

이 장에서는 Bode 플롯을 구성 (그리기)하는 방법을 자세히 이해하겠습니다.

보드 플롯 구성 규칙

Bode 플롯을 구성하는 동안 다음 규칙을 따르십시오.

• 표준 시간 상수 형식으로 개방 루프 전달 함수를 나타냅니다.

• 대용품, $s=j\omega$ 위의 방정식에서.

• 코너 주파수를 찾아 오름차순으로 정렬합니다.

• 1/10로 보드 선도의 시작 주파수를 고려 ^번째 작은 값 중 최소의 코너 주파수의 0.1 라드 / 초 및 10 배 최대 코너 주파수 개까지 보데 그래프를 그린다.

• 각 항에 대한 크기 도표를 그리고이 도표를 적절하게 결합하십시오.

• 각 항에 대한 위상 도표를 그리고이 도표를 적절하게 결합하십시오.

Note − 코너 주파수는 크기 플롯의 기울기에 변화가있는 주파수입니다.

예

폐쇄 루프 제어 시스템의 개방 루프 전달 함수를 고려하십시오.

$$G(s)H(s)=\frac{10s}{(s+2)(s+5)}$$

이 개방 루프 전달 함수를 표준 시간 상수 형식으로 변환 해 보겠습니다.

$$G(s)H(s)=\frac{10s}{2\left( \frac{s}{2}+1 \right )5 \left( \frac{s}{5}+1 \right )}$$

$$\Rightarrow G(s)H(s)=\frac{s}{\left( 1+\frac{s}{2} \right )\left( 1+\frac{s}{5} \right )}$$

따라서 앞에서 언급 한 규칙을 사용하여 세미 로그 시트에 Bode 플롯을 그릴 수 있습니다.

보드 플롯을 사용한 안정성 분석

Bode 플롯에서 이러한 매개 변수의 값을 기반으로 제어 시스템이 안정적인지, 약간 안정적인지 또는 불안정한 지 여부를 알 수 있습니다.

• 주파수에 대한 교차 주파수 및 주파수에 대한 위상 교차 이득
• 이익 마진 및 위상 마진

주파수에 대한 위상 교차

위상 플롯의 위상이 -180 ^{0 인} 주파수는 다음과 같이 알려져 있습니다.phase cross over frequency. 다음과 같이 표시됩니다.$\omega_{pc}$. 주파수에 대한 위상 교차의 단위는 다음과 같습니다.rad/sec.

주파수를 통한 이득 교차

크기 플롯의 크기가 0dB 인 주파수는 다음과 같이 알려져 있습니다. gain cross over frequency. 다음과 같이 표시됩니다.$\omega_{gc}$. 주파수를 통한 이득 교차의 단위는 다음과 같습니다.rad/sec.

위상 크로스 오버 주파수와 게인 크로스 오버 주파수 사이의 관계를 기반으로 한 제어 시스템의 안정성은 다음과 같습니다.

• 위상이 주파수에 교차하는 경우 $\omega_{pc}$ 게인 크로스 오버 주파수보다 큽니다. $\omega_{gc}$, 제어 시스템은 stable.

• 위상이 주파수에 교차하는 경우 $\omega_{pc}$ 게인 크로스 오버 주파수와 같습니다. $\omega_{gc}$, 제어 시스템은 marginally stable.

• 위상이 주파수에 교차하는 경우 $\omega_{pc}$ 게인 크로스 오버 주파수보다 작습니다. $\omega_{gc}$, 제어 시스템은 unstable.

이익 마진

이익 마진 $GM$ 위상 교차 주파수에서 dB 단위의 음의 크기와 같습니다.

$$GM=20\log\left( \frac{1}{M_{pc}}\right )=20logM_{pc}$$

어디, $M_{pc}$주파수에 대한 위상 교차의 크기입니다. 이득 마진 (GM)의 단위는dB.

위상 마진

위상 마진 공식 $PM$ 이다

$$PM=180^0+\phi_{gc}$$

어디, $\phi_{gc}$게인 크로스 오버 주파수에서의 위상 각입니다. 위상 마진의 단위는degrees.

게인 마진과 위상 마진의 관계에 따른 제어 시스템의 안정성은 다음과 같습니다.

• 두 이익 마진이 $GM$ 및 위상 마진 $PM$ 긍정적이면 제어 시스템은 stable.

• 두 이익 마진이 $GM$ 및 위상 마진 $PM$ 0과 같으면 제어 시스템은 marginally stable.

• 이익 마진이 $GM$ 및 / 또는 위상 마진 $PM$ 부정적이면 제어 시스템은 unstable.

이전 장에서 Bode 플롯에 대해 논의했습니다. 여기에는 주파수 함수로서 크기와 위상에 대한 두 개의 개별 플롯이 있습니다. 이제 극좌표에 대해 논의하겠습니다. 극좌표는 크기와 위상 사이에서 그릴 수있는 플롯입니다. 여기서 크기는 정상 값으로 만 표시됩니다.

극지 형태 $G(j\omega)H(j\omega)$ 이다

$$G(j\omega)H(j\omega)=|G(j\omega)H(j\omega)| \angle G(j\omega)H(j\omega)$$

그만큼 Polar plot 크기와 위상 각 사이에서 그릴 수있는 플롯입니다. $G(j\omega)H(j\omega)$ 다양하게 $\omega$0에서 ∞까지. 폴라 그래프 시트는 다음 그림에 나와 있습니다.

이 그래프 시트는 동심원과 방사형 선으로 구성됩니다. 그만큼concentric circles 그리고 radial lines각각 크기와 위상 각을 나타냅니다. 이러한 각도는 반 시계 방향의 양수 값으로 표시됩니다. 마찬가지로 시계 방향으로 음수 값으로 각도를 나타낼 수 있습니다. 예를 들어, 시계 반대 방향 의 각도 270 ⁰ 은 시계 방향의 각도 −90 ⁰ 과 같습니다 .

극좌표 플롯을 그리기위한 규칙

극좌표를 플로팅하려면 다음 규칙을 따르십시오.

• 대용품, $s = j\omega$ 개방 루프 전달 함수에서.

• 크기와 위상에 대한 표현식을 작성하십시오. $G(j\omega)H(j\omega)$.

• 시작 크기와 위상을 찾으십시오. $G(j\omega)H(j\omega)$ 대체하여 $\omega = 0$. 따라서 극좌표는이 크기와 위상 각으로 시작됩니다.

• 끝 크기와 위상을 찾으십시오. $G(j\omega)H(j\omega)$ 대체하여 $\omega = \infty$. 따라서 극좌표는이 크기와 위상 각으로 끝납니다.

• 가상의 항을 만들어 극좌표가 실제 축과 교차하는지 확인하십시오. $G(j\omega)H(j\omega)$ 0과 같고 값을 찾으십시오. $\omega$.

• 실제 항을 만들어 극좌표가 가상 축과 교차하는지 확인하십시오. $G(j\omega)H(j\omega)$ 0과 같고 값을 찾으십시오. $\omega$.

• 극좌표를 더 명확하게 그리기 위해 크기와 위상을 찾으십시오. $G(j\omega)H(j\omega)$ 다른 가치를 고려하여 $\omega$.

예

폐쇄 루프 제어 시스템의 개방 루프 전달 함수를 고려하십시오.

$$G(s)H(s)=\frac{5}{s(s+1)(s+2)}$$

위의 규칙을 사용하여이 제어 시스템의 극좌표를 그리겠습니다.

Step 1 − 대체, $s = j\omega$ 개방 루프 전달 함수에서.

$$G(j\omega)H(j\omega)=\frac{5}{j\omega(j\omega+1)(j\omega+2)}$$

개방 루프 전달 함수의 크기는 다음과 같습니다.

$$M=\frac{5}{\omega(\sqrt{\omega^2+1})(\sqrt{\omega^2+4})}$$

개방 루프 전달 함수의 위상 각은 다음과 같습니다.

$$\phi=-90^0-\tan^{-1}\omega-\tan^{-1}\frac{\omega}{2}$$

Step 2 − 다음 표는 개방 루프 전달 함수의 크기와 위상 각을 보여줍니다. $\omega = 0$ rad / sec 및 $\omega = \infty$ rad / 초

주파수 (rad / sec)	크기	위상 각 (도)
0	∞	-90 또는 270
∞	0	-270 또는 90

따라서 극좌표 플롯은 (∞, −90 ⁰ )에서 시작하고 (0, −270 ⁰ ) 에서 끝납니다 . 괄호 안의 첫 번째와 두 번째 항은 각각 크기와 위상 각을 나타냅니다.

Step 3− 시작 및 끝 극좌표를 기반으로이 극좌표는 음의 실수 축과 교차합니다. 음의 실수 축에 해당하는 위상 각은 −180 ⁰ 또는 180 ⁰ 입니다. 따라서 개 루프 전달 함수의 위상 각을 −180 ⁰ 또는 180 ⁰ 으로 동일시 하면$\omega$ 가치 $\sqrt{2}$.

대체함으로써 $\omega = \sqrt{2}$ 개방 루프 전달 함수의 크기에서 우리는 $M = 0.83$. 따라서 극좌표는 다음과 같은 경우 음의 실수 축과 교차합니다.$\omega = \sqrt{2}$극좌표는 (0.83, −180 ⁰ )입니다.

따라서 극좌표에 위의 정보로 극좌표를 그릴 수 있습니다.

Nyquist 플롯은 ω를 −∞에서 ∞로 변경하여 폐쇄 루프 제어 시스템의 안정성을 찾기위한 극지 플롯의 연속입니다. 즉, Nyquist 플롯은 개방 루프 전달 함수의 완전한 주파수 응답을 그리는 데 사용됩니다.

나이 퀴 스트 안정성 기준

Nyquist 안정성 기준은 principle of argument. P 극이 있고 Z 0이 's'평면 폐쇄 경로로 둘러싸여 있으면 해당$G(s)H(s)$ 평면은 원점을 둘러싸 야합니다. $P − Z$타임스. 그래서 우리는 둘러싸 기 N의 수를 다음과 같이 쓸 수 있습니다.

$$N=P-Z$$

• 동봉 된 's'평면 폐쇄 경로에 극만 포함 된 경우 $G(s)H(s)$ 평면은 's'평면에서 닫힌 경로의 방향과 반대입니다.

• 포함 된 's'평면의 닫힌 경로에 0 만 포함되어있는 경우 $G(s)H(s)$ 평면은 's'평면의 닫힌 경로와 같은 방향이됩니다.

이제 's'평면을 닫힌 경로로 선택하여 's'평면의 전체 오른쪽 절반에 인수의 원리를 적용 해 보겠습니다. 이 선택된 경로를Nyquist 윤곽.

폐 루프 전달 함수의 모든 극이 's'평면의 왼쪽 절반에 있으면 폐 루프 제어 시스템이 안정적이라는 것을 알고 있습니다. 따라서 폐 루프 전달 함수의 극점은 특성 방정식의 근본 일뿐입니다. 특성 방정식의 차수가 증가함에 따라 근을 찾기가 어렵습니다. 따라서 다음과 같이 특성 방정식의 이러한 뿌리를 연관시켜 보겠습니다.

• 특성 방정식의 극점은 개방 루프 전달 함수의 극점과 동일합니다.

• 특성 방정식의 0은 폐 루프 전달 함수의 극점과 동일합니다.

우리는 's'평면의 오른쪽 절반에 개방 루프 극이없는 경우 개방 루프 제어 시스템이 안정적이라는 것을 알고 있습니다.

즉,$P=0 \Rightarrow N=-Z$

우리는 's'평면의 오른쪽 절반에 폐쇄 루프 폴이 없으면 폐쇄 루프 제어 시스템이 안정적이라는 것을 알고 있습니다.

즉,$Z=0 \Rightarrow N=P$

Nyquist stability criterion임계점 (1 + j0)에 대한 둘러싸 기의 수는 's'평면의 오른쪽 절반에있는 개방 루프 전달 함수의 극에 불과한 특성 방정식의 극과 동일해야합니다. 원점에서 (1 + j0) 로의 이동은 특성 방정식 평면을 제공합니다.

Nyquist 플롯 그리기 규칙

Nyquist 플롯을 플로팅하려면 다음 규칙을 따르십시오.

• 개방 루프 전달 함수의 극점과 영점을 찾습니다. $G(s)H(s)$ 's'비행기에서.

• 다양한 방식으로 극좌표 그리기 $\omega$0에서 무한대로. s = 0에 극점 또는 영점이 있으면 변화$\omega$ 극좌표를 그리기 위해 0+에서 무한대까지.

• 값에 대한 극좌표 위의 미러 이미지를 그립니다. $\omega$범위는 −∞에서 0까지입니다 ( 극이 있으면 0 ⁻ s = 0에 0이있는 경우).

• 무한 반경 반원의 수는 원점의 극 또는 0의 수와 같습니다. 무한 반경 반원은 극좌표의 미러 이미지가 끝나는 지점에서 시작됩니다. 그리고이 무한 반경 반원은 극좌표가 시작되는 지점에서 끝납니다.

Nyquist 플롯을 그린 후 Nyquist 안정성 기준을 사용하여 폐쇄 루프 제어 시스템의 안정성을 찾을 수 있습니다. 임계점 (-1 + j0)이 외곽선 밖에 있으면 폐쇄 루프 제어 시스템이 절대적으로 안정적입니다.

Nyquist 플롯을 사용한 안정성 분석

Nyquist 플롯에서 이러한 매개 변수의 값을 기반으로 제어 시스템이 안정적인지, 약간 안정적인지 또는 불안정한지를 식별 할 수 있습니다.

• 주파수에 대한 교차 주파수 및 주파수에 대한 위상 교차 이득
• 이익 마진 및 위상 마진

주파수에 대한 위상 교차

Nyquist 플롯이 음의 실수 축과 교차하는 주파수 (위상 각은 180 ⁰ )는 다음과 같이 알려져 있습니다.phase cross over frequency. 다음과 같이 표시됩니다.$\omega_{pc}$.

주파수를 통한 이득 교차

나이 퀴 스트 플롯이 1의 크기를 갖는 주파수는 gain cross over frequency. 다음과 같이 표시됩니다.$\omega_{gc}$.

주파수에 대한 위상 교차와 주파수에 대한 이득 교차 사이의 관계에 기반한 제어 시스템의 안정성은 다음과 같습니다.

• 위상이 주파수에 교차하는 경우 $\omega_{pc}$ 게인 크로스 오버 주파수보다 큽니다. $\omega_{gc}$, 제어 시스템은 stable.

• 위상이 주파수에 교차하는 경우 $\omega_{pc}$ 게인 크로스 오버 주파수와 같습니다. $\omega_{gc}$, 제어 시스템은 marginally stable.

• 주파수에 위상 교차하는 경우 $\omega_{pc}$ 게인 크로스 오버 주파수보다 작음 $\omega_{gc}$, 제어 시스템은 unstable.

이익 마진

이득 마진 $GM$ 주파수에 대한 위상 교차에서 Nyquist 플롯 크기의 역수와 같습니다.

$$GM=\frac{1}{M_{pc}}$$

어디, $M_{pc}$ 주파수에 대한 위상 교차에서 정상 스케일의 크기입니다.

위상 마진

위상 마진 $PM$180 ⁰ 과 게인 크로스 오버 주파수에서의 위상 각 의 합과 같습니다 .

$$PM=180^0+\phi_{gc}$$

어디, $\phi_{gc}$ 게인 크로스 오버 주파수에서의 위상 각입니다.

게인 마진과 위상 마진의 관계를 기반으로 한 제어 시스템의 안정성은 다음과 같습니다.

• 이익 마진이 $GM$ 1보다 크고 위상 마진 $PM$ 긍정적이면 제어 시스템은 stable.

• 이익 마진이 $GM$ 1과 같고 위상 마진 $PM$ 0도이면 제어 시스템은 marginally stable.

• 이익 마진이 $GM$ 1 미만 및 / 또는 위상 마진 $PM$ 음수이면 제어 시스템이 unstable.

보상기에는 지연, 리드 및 지연 리드 보상기의 세 가지 유형이 있습니다. 이들은 가장 일반적으로 사용됩니다.

지연 보상기

지연 보상기는 정현파 입력이 적용될 때 위상 지연이있는 정현파 출력을 생성하는 전기 네트워크입니다. 's'영역의 지연 보상기 회로는 다음 그림에 나와 있습니다.

여기서 커패시터는 저항과 직렬로 연결됩니다. $R_2$ 출력은이 조합에서 측정됩니다.

이 지연 보상기의 전달 함수는 다음과 같습니다.

$$\frac{V_o(s)}{V_i(s)}=\frac{1}{\alpha} \left( \frac{s+\frac{1}{\tau}}{s+\frac{1}{\alpha\tau}} \right )$$

어디,

$$\tau=R_2C$$

$$\alpha=\frac{R_1+R_2}{R_2}$$

위의 방정식에서 $\alpha$ 항상 1보다 큽니다.

전달 함수에서 지연 보상기가 한 극을 가지고 있다는 결론을 내릴 수 있습니다. $s = − \frac{1}{\alpha \tau}$ 그리고 하나의 0 $s = −\frac{1}{\tau}$. 즉, 지연 보상기의 극점 영점 구성에서 극점이 원점에 더 가까워집니다.

대용품, $s = j\omega$ 전달 함수에서.

$$\frac{V_o(j\omega)}{V_i(j\omega)}=\frac{1}{\alpha}\left( \frac{j\omega+\frac{1}{\tau}}{j\omega+\frac{1}{\alpha\tau}}\right )$$

위상 각도 $\phi = \tan^{−1} \omega\tau − tan^{−1} \alpha\omega\tau$

출력 정현파 신호의 위상은 입력 정현파 신호와 전달 함수의 위상 각도의 합과 같습니다.

따라서이 보상기의 출력에서 ​​위상 지연을 생성하려면 전달 함수의 위상 각도가 음수 여야합니다. 이것은 때 발생합니다$\alpha > 1$.

리드 보상기

리드 보상기는 사인파 입력이 적용될 때 위상 리드를 갖는 사인파 출력을 생성하는 전기 네트워크입니다. 's'도메인의 리드 보상기 회로가 다음 그림에 나와 있습니다.

여기서 커패시터는 저항과 병렬입니다. $R_1$ 출력은 저항 $ R_2에서 측정됩니다.

이 리드 보상기의 전달 함수는 다음과 같습니다.

$$ \ frac {V_o (s)} {V_i (s)} = \ beta \ left (\ frac {s \ tau + 1} {\ beta s \ tau + 1} \ right) $$

어디,

$$ \ tau = R_1C $$

$$ \ beta = \ frac {R_2} {R_1 + R_2} $$

전달 함수에서 리드 보상기가 $ s = − \ frac {1} {\ beta}에 극점을 갖는다는 결론을 내릴 수 있습니다.$ and zero at $s = − \ frac {1} {\ beta \ tau} $.

전달 함수에서 $ s = j \ omega $를 대체합니다.

$$ \ frac {V_o (j \ omega)} {V_i (j \ omega)} = \ beta \ left (\ frac {j \ omega \ tau + 1} {\ beta j \ omega \ tau + 1} \ right ) $$

위상 각 $ \ phi = tan ^ {− 1} \ omega \ tau − tan ^ {− 1} \ beta \ omega \ tau $

출력 정현파 신호의 위상은 입력 정현파 신호와 전달 함수의 위상 각도의 합과 같습니다.

따라서이 보상기의 출력에서 ​​위상 리드를 생성하려면 전달 함수의 위상 각도가 양수 여야합니다. 이는 $ 0 <\ beta <1 $ 일 때 발생합니다. 따라서 리드 보상기의 극점 영점 구성에서 0은 원점에 더 가깝습니다.

지연 리드 보상기

지연 리드 보상기는 한 주파수 영역에서 위상 지연을 생성하고 다른 주파수 영역에서 위상 리드를 생성하는 전기 네트워크입니다. 지연 및 리드 보상기의 조합입니다. 's'영역의 지연 리드 보상기 회로는 다음 그림에 나와 있습니다.

이 회로는 두 보상기가 모두 계단식으로 연결된 것처럼 보입니다. 따라서이 회로의 전달 함수는 리드 및 지연 보상기의 전달 함수의 곱이됩니다.

$$ \ frac {V_o (s)} {V_i (s)} = \ beta \ left (\ frac {s \ tau_1 + 1} {\ beta s \ tau_1 + 1} \ right) \ frac {1} {\ alpha} \ left (\ frac {s + \ frac {1} {\ tau_2}} {s + \ frac {1} {\ alpha \ tau_2}} \ right) $$

우리는 $ \ alpha \ beta = 1 $을 알고 있습니다.

$$ \ Rightarrow \ frac {V_o (s)} {V_i (s)} = \ left (\ frac {s + \ frac {1} {\ tau_1}} {s + \ frac {1} {\ beta \ tau_1}} \ right) \ left (\ frac {s + \ frac {1} {\ tau_2}} {s + \ frac {1} {\ alpha \ tau_2}} \ right) $$

어디,

$$ \ tau_1 = R_1C_1 $$

$$ \ tau_2 = R_2C_2 $$

제어 시스템의 성능을 향상시키기 위해 다양한 유형의 컨트롤러가 사용됩니다. 이 장에서는 비례, 미분 및 적분 컨트롤러와 같은 기본 컨트롤러에 대해 설명합니다.

비례 컨트롤러

비례 컨트롤러는 오류 신호에 비례하는 출력을 생성합니다.

$$ u (t) \ propto e (t) $$

$$ \ 오른쪽 화살표 u (t) = K_P e (t) $$

양쪽에 라플라스 변환 적용-

$$ U (s) = K_P E (s) $$

$$ \ frac {U (s)} {E (s)} = K_P $$

따라서 비례 컨트롤러의 전달 함수는 $ K_P $입니다.

어디,

U (s)는 작동 신호 u (t)의 라플라스 변환입니다.

E (s)는 오류 신호 e (t)의 라플라스 변환입니다.

K _P 는 비례 상수입니다.

비례 컨트롤러와 함께 유니티 네거티브 피드백 폐쇄 루프 제어 시스템의 블록 다이어그램이 다음 그림에 나와 있습니다.

비례 컨트롤러는 요구 사항에 따라 과도 응답을 변경하는 데 사용됩니다.

파생 컨트롤러

미분 컨트롤러는 오류 신호의 미분 출력을 생성합니다.

$$ u (t) = K_D \ frac {\ text {d} e (t)} {\ text {d} t} $$

양쪽에 라플라스 변환을 적용합니다.

$$ U (s) = K_D sE (s) $$

$$ \ frac {U (s)} {E (s)} = K_D s $$

따라서 미분 컨트롤러의 전달 함수는 $ K_D s $입니다.

여기서 $ K_D $는 미분 상수입니다.

미분 컨트롤러와 함께 유니티 네거티브 피드백 폐쇄 루프 제어 시스템의 블록 다이어그램이 다음 그림에 나와 있습니다.

미분 제어기는 불안정한 제어 시스템을 안정된 제어 시스템으로 만들기 위해 사용됩니다.

통합 컨트롤러

적분 컨트롤러는 오류 신호의 적분 인 출력을 생성합니다.

$$ u (t) = K_I \ int e (t) dt $$

양쪽에 라플라스 변환 적용-

$$ U (s) = \ frac {K_I E (s)} {s} $$

$$ \ frac {U (s)} {E (s)} = \ frac {K_I} {s} $$

따라서 적분 컨트롤러의 전달 함수는 $ \ frac {K_I} {s} $입니다.

여기서 $ K_I $는 정수 상수입니다.

통합 컨트롤러와 함께 통합 네거티브 피드백 폐쇄 루프 제어 시스템의 블록 다이어그램은 다음 그림에 나와 있습니다.

통합 컨트롤러는 정상 상태 오류를 줄이는 데 사용됩니다.

이제 기본 컨트롤러의 조합에 대해 논의하겠습니다.

PD (Proportional Derivative) 컨트롤러

비례 미분 제어기는 비례 및 미분 제어기의 출력 조합 인 출력을 생성합니다.

$$ u (t) = K_P e (t) + K_D \ frac {\ text {d} e (t)} {\ text {d} t} $$

양쪽에 라플라스 변환 적용-

$$ U (s) = (K_P + K_D s) E (s) $$

$$ \ frac {U (s)} {E (s)} = K_P + K_D s $$

따라서 비례 미분 제어기의 전달 함수는 $ K_P + K_D s $입니다.

비례 미분 컨트롤러와 함께 유니티 네거티브 피드백 폐쇄 루프 제어 시스템의 블록 다이어그램이 다음 그림에 나와 있습니다.

비례 미분 컨트롤러는 정상 상태 오류에 영향을주지 않고 제어 시스템의 안정성을 향상시키는 데 사용됩니다.

비례 적분 (PI) 컨트롤러

비례 적분 컨트롤러는 비례 및 적분 컨트롤러의 출력 조합 인 출력을 생성합니다.

$$ u (t) = K_P e (t) + K_I \ int e (t) dt $$

양쪽에 라플라스 변환 적용-

$$ U (s) = \ left (K_P + \ frac {K_I} {s} \ 오른쪽) E (s) $$

$$ \ frac {U (s)} {E (s)} = K_P + \ frac {K_I} {s} $$

따라서 비례 적분 제어기의 전달 함수는 $ K_P + \ frac {K_I} {s} $입니다.

비례 적분 컨트롤러와 함께 유니티 네거티브 피드백 폐쇄 루프 제어 시스템의 블록 다이어그램은 다음 그림에 나와 있습니다.

비례 적분 컨트롤러는 제어 시스템의 안정성에 영향을주지 않고 정상 상태 오류를 줄이는 데 사용됩니다.

비례 적분 미분 (PID) 컨트롤러

비례 적분 미분 제어기는 비례, 적분 및 미분 제어기의 출력 조합 인 출력을 생성합니다.

$$ u (t) = K_P e (t) + K_I \ int e (t) dt + K_D \ frac {\ text {d} e (t)} {\ text {d} t} $$

양쪽에 라플라스 변환 적용-

$$ U (s) = \ left (K_P + \ frac {K_I} {s} + K_D s \ right) E (s) $$

$$ \ frac {U (s)} {E (s)} = K_P + \ frac {K_I} {s} + K_D s $$

따라서 비례 적분 미분 제어기의 전달 함수는 $ K_P + \ frac {K_I} {s} + K_D s $입니다.

다음 그림은 비례 적분 미분 컨트롤러와 함께 유니티 네거티브 피드백 폐쇄 루프 제어 시스템의 블록 다이어그램입니다.

비례 적분 미분 컨트롤러는 제어 시스템의 안정성을 개선하고 정상 상태 오류를 줄이는 데 사용됩니다.

그만큼 state space model LTI (Linear Time-Invariant) 시스템은 다음과 같이 나타낼 수 있습니다.

$$ \ dot {X} = AX + BU $$

$$ Y = CX + DU $$

첫 번째와 두 번째 방정식은 각각 상태 방정식과 출력 방정식으로 알려져 있습니다.

어디,

• X와 $ \ dot {X} $는 각각 상태 벡터와 미분 상태 벡터입니다.

• U와 Y는 각각 입력 벡터와 출력 벡터입니다.

• A는 시스템 매트릭스입니다.

• B와 C는 입력 및 출력 행렬입니다.

• D는 피드 포워드 행렬입니다.

상태 공간 모델의 기본 개념

이 장과 관련된 다음 기본 용어입니다.

상태

미래 값 (출력)을 예측하기 위해 시스템의 이력을 요약하는 변수 그룹입니다.

상태 변수

필요한 상태 변수의 수는 시스템에있는 스토리지 요소의 수와 같습니다.

Examples − 인덕터를 통해 흐르는 전류, 커패시터 양단의 전압

상태 벡터

상태 변수를 요소로 포함하는 벡터입니다.

이전 장에서 우리는 제어 시스템의 두 가지 수학적 모델에 대해 논의했습니다. 그것들은 미분 방정식 모델과 전달 함수 모델입니다. 상태 공간 모델은이 두 가지 수학적 모델 중 하나에서 얻을 수 있습니다. 이제이 두 가지 방법을 하나씩 살펴 보겠습니다.

미분 방정식의 상태 공간 모델

다음 시리즈의 RLC 회로를 고려하십시오. 입력 전압 $ v_i (t)$ and the current flowing through the circuit is $i (t) $.

이 회로에는 두 개의 저장 요소 (인덕터와 커패시터)가 있습니다. 따라서 상태 변수의 수는 2 개이고 이러한 상태 변수는 인덕터를 통해 흐르는 전류, $ i (t)입니다.$ and the voltage across capacitor, $v_c (t) $.

회로에서 출력 전압, $ v_0 (t)$ is equal to the voltage across capacitor, $v_c (t) $.

$$ v_0 (t) = v_c (t) $$

루프 주위에 KVL을 적용하십시오.

$$ v_i (t) = Ri (t) + L \ frac {\ text {d} i (t)} {\ text {d} t} + v_c (t) $$

$$ \ Rightarrow \ frac {\ text {d} i (t)} {\ text {d} t} =-\ frac {Ri (t)} {L}-\ frac {v_c (t)} {L} + \ frac {v_i (t)} {L} $$

커패시터 양단의 전압은-

$$ v_c (t) = \ frac {1} {C} \ int i (t) dt $$

시간과 관련하여 위의 방정식을 미분하십시오.

$$ \ frac {\ text {d} v_c (t)} {\ text {d} t} = \ frac {i (t)} {C} $$

상태 벡터, $ X = \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix} $

미분 상태 벡터, $ \ dot {X} = \ begin {bmatrix} \ frac {\ text {d} i (t)} {\ text {d} t} \\\ frac {\ text {d} v_c (t )} {\ text {d} t} \ end {bmatrix} $

미분 방정식과 출력 방정식을 상태 공간 모델의 표준 형식으로 배열 할 수 있습니다.

$$ \ dot {X} = \ begin {bmatrix} \ frac {\ text {d} i (t)} {\ text {d} t} \\\ frac {\ text {d} v_c (t)} { \ text {d} t} \ end {bmatrix} = \ begin {bmatrix}-\ frac {R} {L} &-\ frac {1} {L} \\\ frac {1} {C} & 0 \ end {bmatrix} \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix} + \ begin {bmatrix} \ frac {1} {L} \\ 0 \ end {bmatrix} \ begin {bmatrix } v_i (t) \ end {bmatrix} $$

$$ Y = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix} $$

어디,

$$ A = \ begin {bmatrix}-\ frac {R} {L} &-\ frac {1} {L} \\\ frac {1} {C} & 0 \ end {bmatrix}, \ : B = \ begin {bmatrix} \ frac {1} {L} \\ 0 \ end {bmatrix}, \ : C = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ : 및 \ : D = \ begin {bmatrix } 0 \ end {bmatrix} $$

전달 함수의 상태 공간 모델

분자에있는 항의 유형에 따라 두 가지 유형의 전달 함수를 고려하십시오.

• 분자에 상수 항을 갖는 전달 함수.
• 분자에서 's'의 다항 함수를 갖는 전달 함수.

분자에서 상수 항을 갖는 전달 함수

시스템의 다음 전달 함수를 고려하십시오.

$$ \ frac {Y (s)} {U (s)} = \ frac {b_0} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1s + a_0} $ $

위의 방정식을 다음과 같이 재정렬하십시오.

$$ (s ^ n + a_ {n-1} s ^ {n-1} + ... + a_0) Y (s) = b_0 U (s) $$

양쪽에 역 라플라스 변환을 적용합니다.

$$ \ frac {\ text {d} ^ ny (t)} {\ text {d} t ^ n} + a_ {n-1} \ frac {\ text {d} ^ {n-1} y (t )} {\ text {d} t ^ {n-1}} + ... + a_1 \ frac {\ text {d} y (t)} {\ text {d} t} + a_0y (t) = b_0 u (t) $$

허락하다

$$ y (t) = x_1 $$

$$ \ frac {\ text {d} y (t)} {\ text {d} t} = x_2 = \ dot {x} _1 $$

$$ \ frac {\ text {d} ^ 2y (t)} {\ text {d} t ^ 2} = x_3 = \ dot {x} _2 $$

$$. $$

$$. $$

$$. $$

$$ \ frac {\ text {d} ^ {n-1} y (t)} {\ text {d} t ^ {n-1}} = x_n = \ dot {x} _ {n-1} $ $

$$ \ frac {\ text {d} ^ ny (t)} {\ text {d} t ^ n} = \ dot {x} _n $$

및 $ u (t) = u $

그때,

$$ \ dot {x} _n + a_ {n-1} x_n + ... + a_1x_2 + a_0x_1 = b_0 u $$

위의 방정식에서 다음과 같은 상태 방정식을 작성할 수 있습니다.

$$ \ dot {x} _n = -a_0x_1-a_1x_2 -...- a_ {n-1} x_n + b_0 u $$

출력 방정식은-

$$ y (t) = y = x_1 $$

상태 공간 모델은 다음과 같습니다.

$ \ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \\\ vdots \\\ dot {x} _ {n-1} \\\ dot {x} _n \ end {bmatrix} $

$$ = \ begin {bmatrix} 0 & 1 & 0 & \ dotso & 0 & 0 \\ 0 & 0 & 1 & \ dotso & 0 & 0 \\\ vdots & \ vdots & \ vdots & \ dotso & \ vdots & \ vdots \\ 0 & 0 & 0 & \ dotso & 0 & 1 \\-a_0 & -a_1 & -a_2 & \ dotso & -a_ {n-2} & -a_ {n-1} \ end {bmatrix } \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} + \ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 0 \\ b_0 \ end {bmatrix} \ begin {bmatrix} u \ end {bmatrix} $$

$$ Y = \ begin {bmatrix} 1 & 0 & \ dotso & 0 & 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} $$

여기에서 $ D = \ left [0 \ right]. $

예

전달 함수가있는 시스템의 상태 공간 모델을 찾으십시오.

$$ \ frac {Y (s)} {U (s)} = \ frac {1} {s ^ 2 + s + 1} $$

위의 방정식을 다음과 같이 재정렬하십시오.

$$ (s ^ 2 + s + 1) Y (s) = U (s) $$

양쪽에 역 라플라스 변환을 적용합니다.

$$ \ frac {\ text {d} ^ 2y (t)} {\ text {d} t ^ 2} + \ frac {\ text {d} y (t)} {\ text {d} t} + y (t) = u (t) $$

허락하다

$$ y (t) = x_1 $$

$$ \ frac {\ text {d} y (t)} {\ text {d} t} = x_2 = \ dot {x} _1 $$

및 $ u (t) = u $

그러면 상태 방정식은

$$ \ dot {x} _2 = -x_1-x_2 + u $$

출력 방정식은 다음과 같습니다.

$$ y (t) = y = x_1 $$

상태 공간 모델은

$$ \ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} 0 & 1 \\-1 & -1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 0 \\ 1 \ end {bmatrix} \ left [u \ right] $$

$$ Y = \ begin {bmatrix} 1 & 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} $$

분자에서 's'의 다항 함수를 갖는 전달 함수

시스템의 다음 전달 함수를 고려하십시오.

$$ \ frac {Y (s)} {U (s)} = \ frac {b_n s ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0} $$

$$ \ Rightarrow \ frac {Y (s)} {U (s)} = \ left (\ frac {1} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0} \ 오른쪽) (b_n s ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0) $$

위의 방정식은 계단식으로 연결된 두 블록의 전달 함수의 곱 형태입니다.

$$ \ frac {Y (s)} {U (s)} = \ left (\ frac {V (s)} {U (s)} \ right) \ left (\ frac {Y (s)} {V (s)} \ 오른쪽) $$

여기,

$$ \ frac {V (s)} {U (s)} = \ frac {1} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0} $$

위의 방정식을 다음과 같이 재정렬하십시오.

$$ (s ^ n + a_ {n-1} s ^ {n-1} + ... + a_0) V (s) = U (s) $$

양쪽에 역 라플라스 변환을 적용합니다.

$$ \ frac {\ text {d} ^ nv (t)} {\ text {d} t ^ n} + a_ {n-1} \ frac {\ text {d} ^ {n-1} v (t )} {\ text {d} t ^ {n-1}} + ... + a_1 \ frac {\ text {d} v (t)} {\ text {d} t} + a_0v (t) = u (t) $$

허락하다

$$ v (t) = x_1 $$

$$ \ frac {\ text {d} v ((t)} {\ text {d} t} = x_2 = \ dot {x} _1 $$

$$ \ frac {\ text {d} ^ 2v (t)} {\ text {d} t ^ 2} = x_3 = \ dot {x} _2 $$

$$. $$

$$. $$

$$. $$

$$ \ frac {\ text {d} ^ {n-1} v (t)} {\ text {d} t ^ {n-1}} = x_n = \ dot {x} _ {n-1} $ $

$$ \ frac {\ text {d} ^ nv (t)} {\ text {d} t ^ n} = \ dot {x} _n $$

및 $ u (t) = u $

그러면 상태 방정식은

$$ \ dot {x} _n = -a_0x_1-a_1x_2 -...- a_ {n-1} x_n + u $$

중히 여기다,

$$ \ frac {Y (s)} {V (s)} = b_ns ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0 $$

위의 방정식을 다음과 같이 재정렬하십시오.

$$ Y (s) = (b_ns ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0) V (s) $$

양쪽에 역 라플라스 변환을 적용합니다.

$$ y (t) = b_n \ frac {\ text {d} ^ nv (t)} {\ text {d} t ^ n} + b_ {n-1} \ frac {\ text {d} ^ {n -1} v (t)} {\ text {d} t ^ {n-1}} + ... + b_1 \ frac {\ text {d} v (t)} {\ text {d} t} + b_0v (t) $$

위 방정식에서 상태 변수와 $ y (t) = y $를 대체하면 다음과 같은 출력 방정식을 얻을 수 있습니다.

$$ y = b_n \ dot {x} _n + b_ {n-1} x_n + ... + b_1x_2 + b_0x_1 $$

위 방정식에서 $ \ dot {x} _n $ 값을 대입합니다.

$$ y = b_n (-a_0x_1-a_1x_2 -...- a_ {n-1} x_n + u) + b_ {n-1} x_n + ... + b_1x_2 + b_0x_1 $$

$$ y = (b_0-b_na_0) x_1 + (b_1-b_na_1) x_2 + ... + (b_ {n-1} -b_na_ {n-1}) x_n + b_n u $$

상태 공간 모델은

$ \ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \\\ vdots \\\ dot {x} _ {n-1} \\\ dot {x} _n \ end {bmatrix} $

$$ = \ begin {bmatrix} 0 & 1 & 0 & \ dotso & 0 & 0 \\ 0 & 0 & 1 & \ dotso & 0 & 0 \\\ vdots & \ vdots & \ vdots & \ dotso & \ vdots & \ vdots \\ 0 & 0 & 0 & \ dotso & 0 & 1 \\-a_0 & -a_1 & -a_2 & \ dotso & -a_ {n-2} & -a_ {n-1} \ end {bmatrix } \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} + \ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 0 \\ b_0 \ end {bmatrix} \ begin {bmatrix} u \ end {bmatrix} $$

$$ Y = [b_0-b_na_0 \ quad b_1-b_na_1 \ quad ... \ quad b_ {n-2} -b_na_ {n-2} \ quad b_ {n-1} -b_na_ {n-1}] \ 시작 {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} $$

$ b_n = 0 $이면

$$ Y = [b_0 \ quad b_1 \ quad ... \ quad b_ {n-2} \ quad b_ {n-1}] \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n- 1} \\ x_n \ end {bmatrix} $$

이전 장에서 우리는 미분 방정식과 전달 함수에서 상태 공간 모델을 얻는 방법을 배웠습니다. 이 장에서는 상태 공간 모델에서 전달 함수를 얻는 방법에 대해 설명합니다.

상태 공간 모델의 전달 함수

LTI (Linear Time-Invariant) 시스템의 상태 공간 모델은 다음과 같습니다.

$$ \ dot {X} = AX + BU $$

$$ Y = CX + DU $$

상태 방정식의 양쪽에 라플라스 변환을 적용합니다.

$$ sX (s) = AX (s) + BU (s) $$

$$ \ 오른쪽 화살표 (sI-A) X (s) = BU (s) $$

$$ \ 오른쪽 화살표 X (s) = (sI-A) ^ {-1} BU (s) $$

출력 방정식의 양쪽에 라플라스 변환을 적용합니다.

$$ Y (s) = CX (s) + DU (s) $$

위 방정식에서 X (s) 값을 대입합니다.

$$ \ 오른쪽 화살표 Y (s) = C (sI-A) ^ {-1} BU (s) + DU (s) $$

$$ \ 오른쪽 화살표 Y (s) = [C (sI-A) ^ {-1} B + D] U (s) $$

$$ \ Rightarrow \ frac {Y (s)} {U (s)} = C (sI-A) ^ {-1} B + D $$

위의 방정식은 시스템의 전달 함수를 나타냅니다. 따라서 상태 공간 모델에 표시된 시스템에 대해이 공식을 사용하여 시스템의 전달 함수를 계산할 수 있습니다.

Note − $ D = [0] $ 일 때 전달 함수는

$$ \ frac {Y (s)} {U (s)} = C (sI-A) ^ {-1} B $$

Example

상태 공간 모델에 표시된 시스템의 전달 함수를 다음과 같이 계산해 보겠습니다.

$$ \ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} -1 & -1 \\ 1 & 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} [u] $$

$$ Y = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} $$

여기,

$$ A = \ begin {bmatrix} -1 & -1 \\ 1 & 0 \ end {bmatrix}, \ quad B = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix}, \ quad C = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ quad 및 \ quad D = [0] $$

$ D = [0] $ 일 때 전달 함수의 공식은-

$$ \ frac {Y (s)} {U (s)} = C (sI-A) ^ {-1} B $$

위 방정식에서 A, B 및 C 행렬을 대입합니다.

$$ \ frac {Y (s)} {U (s)} = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} s + 1 & 1 \\-1 & s \ end {bmatrix } ^ {-1} \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} $$

$$ \ Rightarrow \ frac {Y (s)} {U (s)} = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ frac {\ begin {bmatrix} s & -1 \\ 1 & s + 1 \ end {bmatrix}} {(s + 1) s-1 (-1)} \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} $$

$$ \ Rightarrow \ frac {Y (s)} {U (s)} = \ frac {\ begin {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} s \\ 1 \ end {bmatrix}} {s ^ 2 + s + 1} = \ frac {1} {s ^ 2 + s + 1} $$

따라서 주어진 상태 공간 모델에 대한 시스템의 전달 함수는 다음과 같습니다.

$$ \ frac {Y (s)} {U (s)} = \ frac {1} {s ^ 2 + s + 1} $$

상태 전이 매트릭스 및 속성

시스템에 초기 조건이있는 경우 출력을 생성합니다. 이 출력은 입력이 없어도 존재하므로zero input response$ x_ {ZIR} (t) $. 수학적으로 다음과 같이 쓸 수 있습니다.

$$ x_ {ZIR} (t) = e ^ {At} X (0) = L ^ {-1} \ left \ {\ left [sI-A \ right] ^ {-1} X (0) \ right \} $$

위의 관계에서 상태 전이 행렬 $ \ phi (t) $를 다음과 같이 작성할 수 있습니다.

$$ \ phi (t) = e ^ {At} = L ^ {-1} [sI-A] ^ {-1} $$

따라서 0 입력 응답은 상태 전이 행렬 $ \ phi (t) $에 초기 조건 행렬을 곱하여 얻을 수 있습니다.

다음은 상태 전이 매트릭스의 속성입니다.

• $ t = 0 $이면 상태 전이 행렬은 단위 행렬과 같습니다.

  $$ \ 파이 (0) = I $$

• 상태 전이 행렬의 역행렬은 't'를 '-t'로 바꾸는 것만으로도 상태 전이 행렬과 동일합니다.

  $$ \ phi ^ {-1} (t) = \ phi (−t) $$

• $ t = t_1 + t_2 인 경우$ , then the corresponding state transition matrix is equal to the multiplication of the two state transition matrices at $t = t_1$ and $t = t_2 $.

  $$ \ phi (t_1 + t_2) = \ phi (t_1) \ phi (t_2) $$

제어 가능성 및 관찰 가능성

이제 제어 시스템의 제어 가능성과 관찰 가능성을 하나씩 살펴 보겠습니다.

제어 가능성

제어 시스템은 controllable 제어 시스템의 초기 상태가 제한된 시간 동안 제어 된 입력에 의해 다른 원하는 상태로 전송 (변경)되는 경우.

제어 시스템의 제어 가능성은 다음을 사용하여 확인할 수 있습니다. Kalman’s test.

• 다음 형식으로 행렬 $ Q_c $를 작성합니다.

  $$ Q_c = \ left [B \ quad AB \ quad A ^ 2B \ quad ... \ quad A ^ {n-1} B \ right] $$

• 행렬 $ Q_c $의 행렬식을 찾아 0이 아니면 제어 시스템을 제어 할 수 있습니다.

관찰 가능성

제어 시스템은 observable 제한된 시간 동안 출력을 관찰하여 제어 시스템의 초기 상태를 결정할 수 있는지 여부.

다음을 사용하여 제어 시스템의 관찰 가능성을 확인할 수 있습니다. Kalman’s test.

• 다음 형식으로 행렬 $ Q_o $를 작성합니다.

  $$ Q_o = \ left [C ^ T \ quad A ^ TC ^ T \ quad (A ^ T) ^ 2C ^ T \ quad ... \ quad (A ^ T) ^ {n-1} C ^ T \ 오른쪽] $$

• 행렬 $ Q_o $의 행렬식을 찾고 0이 아니면 제어 시스템을 관찰 할 수 있습니다.

Example

상태 공간 모델에서 다음과 같이 표현되는 제어 시스템의 제어 가능성과 관찰 가능성을 확인하겠습니다.

$$ \ dot {x} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} -1 & -1 \\ 1 & 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} [u] $$

$$ Y = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} $$

여기,

$$ A = \ begin {bmatrix} -1 & -1 \\ 1 & 0 \ end {bmatrix}, \ quad B = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix}, \ quad \ begin {bmatrix } 0 & 1 \ end {bmatrix}, D = [0] \ quad 및 \ quad n = 2 $$

$ n = 2 인 경우$, the matrix $Q_c $는

$$ Q_c = \ left [B \ quad AB \ right] $$

우리는 행렬 A와 B의 곱을 다음과 같이 얻을 것입니다.

$$ AB = \ begin {bmatrix} -1 \\ 1 \ end {bmatrix} $$

$$ \ Rightarrow Q_c = \ begin {bmatrix} 1 & -1 \\ 0 & 1 \ end {bmatrix} $$

$$ | Q_c | = 1 \ neq 0 $$

행렬 $ Q_c $의 행렬식이 0이 아니므로 주어진 제어 시스템을 제어 할 수 있습니다.

$ n = 2 인 경우$, the matrix $Q_o $는-

$$ Q_o = \ left [C ^ T \ quad A ^ TC ^ T \ right] $$

여기,

$$ A ^ T = \ begin {bmatrix} -1 & 1 \\-1 & 0 \ end {bmatrix} \ quad 및 \ quad C ^ T = \ begin {bmatrix} 0 \\ 1 \ end {bmatrix} $ $

우리는 행렬 $ A ^ T의 곱을 얻을 것입니다$ and $C ^ T $

$$ A ^ TC ^ T = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} $$

$$ \ Rightarrow Q_o = \ begin {bmatrix} 0 & 1 \\ 1 & 0 \ end {bmatrix} $$

$$ \ 오른쪽 화살표 | Q_o | = -1 \ quad \ neq 0 $$

행렬 $ Q_o $의 행렬식이 0이 아니기 때문에 주어진 제어 시스템을 관찰 할 수 있습니다.

따라서 주어진 제어 시스템은 제어 가능하고 관찰 가능합니다.