제어 시스템-시간 응답 분석
시간 영역과 주파수 영역 모두에서 제어 시스템의 응답을 분석 할 수 있습니다. 이후 장에서 제어 시스템의 주파수 응답 분석에 대해 설명합니다. 이제 제어 시스템의 시간 응답 분석에 대해 논의하겠습니다.
시간 응답이란 무엇입니까?
입력에 대한 제어 시스템의 출력이 시간에 따라 변하면 time response제어 시스템의. 시간 응답은 두 부분으로 구성됩니다.
- 일시적인 응답
- 정상 상태 응답
시간 영역에서 제어 시스템의 응답은 다음 그림과 같습니다.

여기에서 과도 및 정상 상태가 그림에 표시됩니다. 이러한 상태에 해당하는 응답을 과도 및 정상 상태 응답이라고합니다.
수학적으로 시간 응답 c (t)를 다음과 같이 작성할 수 있습니다.
$$ c (t) = c_ {tr} (t) + c_ {ss} (t) $$
어디,
- c tr (t)는 과도 응답입니다.
- C의 SS (t)는 정상 상태 반응이다
과도 응답
제어 시스템에 입력을 적용한 후 출력이 정상 상태에 도달하는 데 일정 시간이 걸립니다. 따라서 출력은 정상 상태가 될 때까지 일시적인 상태가됩니다. 따라서 과도 상태에서 제어 시스템의 응답은 다음과 같이 알려져 있습니다.transient response.
과도 응답은 't'값이 큰 경우 0이됩니다. 이상적으로이 't'값은 무한대이며 실제로는 5 배 상수입니다.
수학적으로 다음과 같이 쓸 수 있습니다.
$$ \ lim_ {t \ rightarrow \ infty} c_ {tr} (t) = 0 $$
정상 상태 응답
과도 응답이 큰 't'값에 대해 값이 0 인 후에도 남아있는 시간 응답 부분은 다음과 같이 알려져 있습니다. steady state response. 즉, 정상 상태에서도 과도 응답이 0이됩니다.
Example
제어 시스템 $ c (t) = 10 + 5e ^ {-t} $의 시간 응답에 대한 과도 및 정상 상태 항을 찾아 보겠습니다.
여기서 두 번째 용어 $ 5e ^ {-t} $는 다음과 같이 0이됩니다. t무한대를 나타냅니다. 그래서 이것은transient term. 그리고 첫 번째 학기 10은t무한에 접근합니다. 그래서 이것은steady state term.
표준 테스트 신호
표준 테스트 신호는 임펄스, 스텝, 램프 및 포물선입니다. 이러한 신호는 출력의 시간 응답을 사용하여 제어 시스템의 성능을 파악하는 데 사용됩니다.
단위 임펄스 신호
단위 임펄스 신호, δ (t)는 다음과 같이 정의됩니다.
$ t \ neq 0 $의 경우 $ \ delta (t) = 0 $
및 $ \ int_ {0 ^-} ^ {0 ^ +} \ delta (t) dt = 1 $
다음 그림은 단위 임펄스 신호를 보여줍니다.

따라서 단위 임펄스 신호는 't'가 0 일 때만 존재합니다. 't'주변의 작은 시간 간격에서이 신호의 면적은 0과 같습니다. 단위 임펄스 신호의 값은 't'의 다른 모든 값에 대해 0입니다.
단위 단계 신호
단위 단계 신호 u (t)는 다음과 같이 정의됩니다.
$$ u (t) = 1; t \ geq 0 $$
$ = 0; t <0 $
다음 그림은 단위 단계 신호를 보여줍니다.

따라서 단위 스텝 신호는 0을 포함한 모든 양의 't'값에 대해 존재합니다. 그리고 그 값은이 간격 동안 1입니다. 단위 스텝 신호의 값은 't'의 모든 음수 값에 대해 0입니다.
단위 램프 신호
단위 램프 신호, r (t)는 다음과 같이 정의됩니다.
$$ r (t) = t; t \ geq 0 $$
$ = 0; t <0 $
단위 램프 신호 $ r (t) $를 단위 스텝 신호로 쓸 수 있습니다. $ u (t) $
$$ r (t) = tu (t) $$
다음 그림은 단위 램프 신호를 보여줍니다.

따라서 단위 램프 신호는 0을 포함한 't'의 모든 양의 값에 대해 존재합니다. 그리고 그 값은이 간격 동안 't'에 대해 선형 적으로 증가합니다. 단위 램프 신호의 값은 't'의 모든 음수 값에 대해 0입니다.
단위 포물선 신호
단위 포물선 신호 p (t)는 다음과 같이 정의됩니다.
$$ p (t) = \ frac {t ^ 2} {2}; t \ geq 0 $$
$ = 0; t <0 $
단위 포물선 신호 $ p (t) $를 단위 스텝 신호로 $ u (t) $로 쓸 수 있습니다.
$$ p (t) = \ frac {t ^ 2} {2} u (t) $$
다음 그림은 단위 포물선 신호를 보여줍니다.
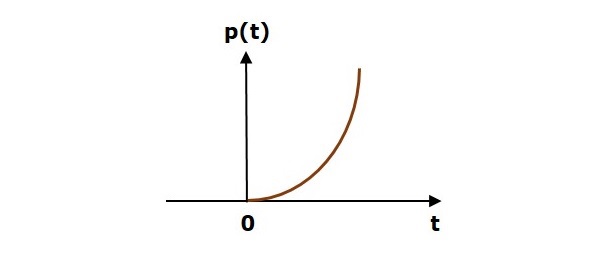
따라서 단위 포물선 신호는 모든 양의 값에 대해 존재합니다. ‘t’0을 포함합니다. 그리고 그 값은이 간격 동안 't'에 대해 비선형 적으로 증가합니다. 단위 포물선 신호의 값은 't'의 모든 음수 값에 대해 0입니다.