퍼스트 오더 시스템의 대응
이 장에서는 1 차 주문 시스템의 시간 응답에 대해 설명하겠습니다. 폐쇄 루프 제어 시스템의 다음 블록 다이어그램을 고려하십시오. 여기에서 개 루프 전달 함수 인 $ \ frac {1} {sT} $는 유니티 네거티브 피드백과 연결됩니다.

우리는 폐쇄 루프 제어 시스템의 전달 함수가 다음과 같이 단일 네거티브 피드백을 갖는다는 것을 알고 있습니다.
$$ \ frac {C (s)} {R (s)} = \ frac {G (s)} {1 + G (s)} $$
위 방정식에서 $ G (s) = \ frac {1} {sT} $를 대입합니다.
$$ \ frac {C (s)} {R (s)} = \ frac {\ frac {1} {sT}} {1+ \ frac {1} {sT}} = \ frac {1} {sT + 1} $$
s의 거듭 제곱은 분모 항에서 1입니다. 따라서 위의 전달 함수는 첫 번째 순서이며 시스템은first order system.
위의 방정식을 다음과 같이 다시 작성할 수 있습니다.
$$ C (s) = \ 왼쪽 (\ frac {1} {sT + 1} \ 오른쪽) R (s) $$
어디,
C(s) 출력 신호 c (t)의 라플라스 변환입니다.
R(s) 입력 신호 r (t)의 라플라스 변환이고,
T 시간 상수입니다.
다음 단계에 따라 시간 도메인에서 1 차 주문 시스템의 응답 (출력)을 얻으십시오.
입력 신호 $ r (t) $의 라플라스 변환을 취하십시오.
방정식 $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
위 방정식에서 $ R (s) $ 값을 대체하십시오.
필요한 경우 $ C (s) $의 부분 분수를 수행하십시오.
$ C (s) $에 역 라플라스 변환을 적용합니다.
이전 장에서 우리는 임펄스, 스텝, 램프 및 포물선과 같은 표준 테스트 신호를 보았습니다. 이제 각 입력에 대한 첫 번째 주문 시스템의 응답을 하나씩 알아 보겠습니다. 응답의 이름은 입력 신호의 이름에 따라 제공됩니다. 예를 들어, 임펄스 입력에 대한 시스템의 응답을 임펄스 응답이라고합니다.
1 차 시스템의 임펄스 응답
고려하다 unit impulse signal 1 차 주문 시스템에 대한 입력으로.
따라서 $ r (t) = \ delta (t) $
양쪽에 라플라스 변환을 적용합니다.
$ R (s) = 1 $
방정식 $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
위 방정식에서 $ R (s) = 1 $를 대입합니다.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) (1) = \ frac {1} {sT + 1} $$
라플라스 변환의 표준 형식 중 하나로 위의 방정식을 다시 정렬하십시오.
$$ C (s) = \ frac {1} {T \ left (\ s + \ frac {1} {T} \ right)} \ 오른쪽 화살표 C (s) = \ frac {1} {T} \ left (\ frac {1} {s + \ frac {1} {T}} \ 오른쪽) $$
양쪽에 역 라플라스 변환을 적용합니다.
$$ c (t) = \ frac {1} {T} e ^ \ left ({-\ frac {t} {T}} \ right) u (t) $$
단위 임펄스 응답은 다음 그림에 나와 있습니다.
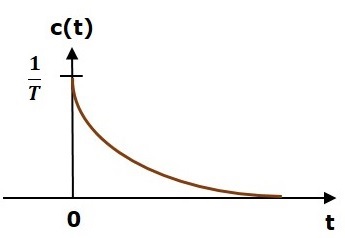
그만큼 unit impulse response, c (t)는 't'의 양수 값에 대한 지수 감쇠 신호이고 't'의 음수 값에 대해서는 0입니다.
첫 주문 시스템의 단계 응답
고려하다 unit step signal 1 차 주문 시스템에 대한 입력으로.
따라서 $ r (t) = u (t) $
양쪽에 라플라스 변환을 적용합니다.
$$ R (s) = \ frac {1} {s} $$
방정식 $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
위 방정식에서 $ R (s) = \ frac {1} {s} $를 대입합니다.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s} \ right) = \ frac {1} {s \ left (sT + 1 \ 오른쪽)} $$
C (s)의 부분 분수를 수행합니다.
$$ C (s) = \ frac {1} {s \ left (sT + 1 \ right)} = \ frac {A} {s} + \ frac {B} {sT + 1} $$
$$ \ Rightarrow \ frac {1} {s \ left (sT + 1 \ right)} = \ frac {A \ left (sT + 1 \ right) + Bs} {s \ left (sT + 1 \ right)} $$
양쪽에서 분모 용어는 동일합니다. 따라서 서로에 의해 취소됩니다. 따라서 분자 항을 동일시하십시오.
$$ 1 = A \ 왼쪽 (sT + 1 \ 오른쪽) + Bs $$
양쪽의 상수 항을 동일시하면 A = 1이됩니다.
A = 1을 대입하고 계수를 동일시하십시오. s 양쪽의 용어.
$$ 0 = T + B \ 오른쪽 화살표 B = -T $$
$ C (s) $의 부분 분수 확장에서 A = 1 및 B = −T를 대입합니다.
$$ C (s) = \ frac {1} {s}-\ frac {T} {sT + 1} = \ frac {1} {s}-\ frac {T} {T \ left (s + \ frac { 1} {T} \ 오른쪽)} $$
$$ \ 오른쪽 화살표 C (s) = \ frac {1} {s}-\ frac {1} {s + \ frac {1} {T}} $$
양쪽에 역 라플라스 변환을 적용합니다.
$$ c (t) = \ left (1-e ^ {-\ left (\ frac {t} {T} \ right)} \ right) u (t) $$
그만큼 unit step response, c (t)에는 과도 및 정상 상태 항이 모두 있습니다.
단위 단계 응답의 과도 조건은 다음과 같습니다.
$$ c_ {tr} (t) =-e ^ {-\ left (\ frac {t} {T} \ right)} u (t) $$
단위 단계 응답의 정상 상태 용어는 다음과 같습니다.
$$ c_ {ss} (t) = u (t) $$
다음 그림은 단위 단계 응답을 보여줍니다.

가치 unit step response, c(t)t = 0이고 t의 모든 음수 값에서 0입니다. 0에서 점차적으로 증가하고 마침내 정상 상태에서 1에 도달합니다. 따라서 정상 상태 값은 입력의 크기에 따라 달라집니다.
1 차 주문 시스템의 램프 응답
고려하다 unit ramp signal 1 차 주문 시스템에 대한 입력으로.
$ 그래서, r (t) = tu (t) $
양쪽에 라플라스 변환을 적용합니다.
$$ R (s) = \ frac {1} {s ^ 2} $$
방정식 $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
위 방정식에서 $ R (s) = \ frac {1} {s ^ 2} $를 대입합니다.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s ^ 2} \ right) = \ frac {1} {s ^ 2 ( sT + 1)} $$
$ C (s) $의 부분 분수를 수행합니다.
$$ C (s) = \ frac {1} {s ^ 2 (sT + 1)} = \ frac {A} {s ^ 2} + \ frac {B} {s} + \ frac {C} {sT +1} $$
$$ \ Rightarrow \ frac {1} {s ^ 2 (sT + 1)} = \ frac {A (sT + 1) + Bs (sT + 1) + Cs ^ 2} {s ^ 2 (sT + 1) } $$
양쪽에서 분모 용어는 동일합니다. 따라서 서로에 의해 취소됩니다. 따라서 분자 항을 동일시하십시오.
$$ 1 = A (sT + 1) + Bs (sT + 1) + Cs ^ 2 $$
양쪽의 상수 항을 동일시하면 A = 1이됩니다.
A = 1을 대입하고 양쪽에있는 s 항의 계수를 동일시하십시오.
$$ 0 = T + B \ 오른쪽 화살표 B = -T $$
유사하게, B = −T를 대입하고 양쪽에서 $ s ^ 2 $ 항의 계수를 동일시하십시오. $ C = T ^ 2 $를 받게됩니다.
$ C (s) $의 부분 분수 전개에서 A = 1, B = −T 및 $ C = T ^ 2 $를 대체합니다.
$$ C (s) = \ frac {1} {s ^ 2}-\ frac {T} {s} + \ frac {T ^ 2} {sT + 1} = \ frac {1} {s ^ 2} -\ frac {T} {s} + \ frac {T ^ 2} {T \ left (s + \ frac {1} {T} \ right)} $$
$$ \ Rightarrow C (s) = \ frac {1} {s ^ 2}-\ frac {T} {s} + \ frac {T} {s + \ frac {1} {T}} $$
양쪽에 역 라플라스 변환을 적용합니다.
$$ c (t) = \ left (t-T + Te ^ {-\ left (\ frac {t} {T} \ right)} \ right) u (t) $$
그만큼 unit ramp response, c (t)에는 과도 및 정상 상태 항이 모두 있습니다.
단위 램프 응답의 과도 조건은 다음과 같습니다.
$$ c_ {tr} (t) = Te ^ {-\ left (\ frac {t} {T} \ right)} u (t) $$
단위 램프 응답의 정상 상태 용어는 다음과 같습니다.
$$ c_ {ss} (t) = (tT) u (t) $$
다음 그림은 단위 램프 응답을 보여줍니다.

그만큼 unit ramp response, c (t)는 t의 모든 양수 값에 대해 단위 램프 입력 신호를 따릅니다. 그러나 입력 신호에서 T 단위의 편차가 있습니다.
1 차 시스템의 포물선 응답
고려하다 unit parabolic signal 1 차 주문 시스템에 대한 입력으로.
따라서 $ r (t) = \ frac {t ^ 2} {2} u (t) $
양쪽에 라플라스 변환을 적용합니다.
$$ R (s) = \ frac {1} {s ^ 3} $$
방정식 $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
위 방정식에서 $ R (s) = \ frac {1} {s ^ 3} $를 대체합니다.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s ^ 3} \ right) = \ frac {1} {s ^ 3 ( sT + 1)} $$
$ C (s) $의 부분 분수를 수행합니다.
$$ C (s) = \ frac {1} {s ^ 3 (sT + 1)} = \ frac {A} {s ^ 3} + \ frac {B} {s ^ 2} + \ frac {C} {s} + \ frac {D} {sT + 1} $$
단순화 한 후 A, B, C 및 D의 값을 각각 1, $ -T, \ : T ^ 2 \ : 및 \ : −T ^ 3 $로 얻습니다. 위의 C (s) 부분 분수 확장에서이 값을 대체합니다.
$ C (s) = \ frac {1} {s ^ 3}-\ frac {T} {s ^ 2} + \ frac {T ^ 2} {s}-\ frac {T ^ 3} {sT + 1 } \ : \ Rightarrow C (s) = \ frac {1} {s ^ 3}-\ frac {T} {s ^ 2} + \ frac {T ^ 2} {s}-\ frac {T ^ 2} {s + \ frac {1} {T}} $
양쪽에 역 라플라스 변환을 적용합니다.
$$ c (t) = \ left (\ frac {t ^ 2} {2} -Tt + T ^ 2-T ^ 2e ^ {-\ left (\ frac {t} {T} \ right)} \ right ) u (t) $$
그만큼 unit parabolic response, c (t)에는 과도 및 정상 상태 항이 모두 있습니다.
단위 포물선 응답의 과도 항은 다음과 같습니다.
$$ C_ {tr} (t) =-T ^ 2e ^ {-\ left (\ frac {t} {T} \ right)} u (t) $$
단위 포물선 응답의 정상 상태 항은 다음과 같습니다.
$$ C_ {ss} (t) = \ left (\ frac {t ^ 2} {2} -Tt + T ^ 2 \ right) u (t) $$
이러한 응답으로부터 우리는 1 차 제어 시스템이 램프 및 포물선 형 입력으로 안정적이지 않다는 결론을 내릴 수 있습니다. 이러한 응답은 무한한 시간에도 계속 증가하기 때문입니다. 1 차 제어 시스템은 이러한 응답이 제한된 출력을 갖기 때문에 임펄스 및 단계 입력으로 안정적입니다. 그러나 임펄스 응답에는 정상 상태 항이 없습니다. 따라서 단계 신호는 응답으로부터 제어 시스템을 분석하기 위해 시간 영역에서 널리 사용됩니다.