Cyfrowe przetwarzanie sygnału - krótki przewodnik
Definicja
Wszystko, co przenosi informacje, można nazwać sygnałem. Można go również zdefiniować jako wielkość fizyczną, która zmienia się wraz z czasem, temperaturą, ciśnieniem lub dowolnymi zmiennymi niezależnymi, takimi jak sygnał mowy lub sygnał wideo.
Proces działania, w którym charakterystyka sygnału (amplituda, kształt, faza, częstotliwość, itp.) Ulega zmianie, nazywany jest przetwarzaniem sygnału.
Note- Każdy niechciany sygnał zakłócający główny sygnał nazywany jest szumem. Zatem szum jest również sygnałem, ale niepożądanym.
Zgodnie z ich reprezentacją i przetwarzaniem, sygnały można podzielić na różne kategorie, których szczegóły omówiono poniżej.
Ciągłe sygnały czasu
Sygnały czasu ciągłego są definiowane wzdłuż kontinuum czasu, a zatem są reprezentowane przez ciągłą zmienną niezależną. Sygnały czasu ciągłego są często nazywane sygnałami analogowymi.
Ten typ sygnału wykazuje ciągłość zarówno pod względem amplitudy, jak i czasu. Będą one miały wartości w każdej chwili. Funkcje sinus i cosinus są najlepszym przykładem ciągłego sygnału czasu.
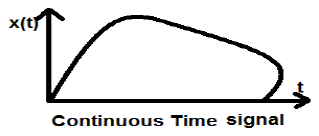
Sygnał pokazany powyżej jest przykładem ciągłego sygnału czasowego, ponieważ możemy uzyskać wartość sygnału w każdej chwili.
Sygnały czasu dyskretnego
Sygnały, które są definiowane dyskretnie, nazywane są sygnałami dyskretnymi. Dlatego każda zmienna niezależna ma odrębną wartość. W ten sposób są przedstawiane jako sekwencje liczb.
Chociaż sygnały mowy i wideo mają przywilej reprezentowania zarówno w formacie czasu ciągłego, jak i dyskretnego; w pewnych okolicznościach są identyczne. Amplitudy również wykazują charakterystykę dyskretną. Doskonałym tego przykładem jest sygnał cyfrowy; których amplituda i czas są dyskretne.
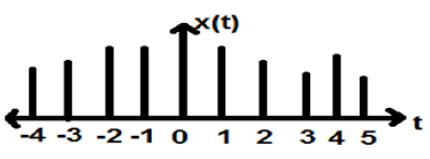
Powyższy rysunek przedstawia dyskretną charakterystykę amplitudy sygnału dyskretnego w okresie czasu. Matematycznie te typy sygnałów można sformułować jako;
$$x = \left \{ x\left [ n \right ] \right \},\quad -\infty < n< \infty$$Gdzie n jest liczbą całkowitą.
Jest to ciąg liczb x, gdzie n- ta liczba w ciągu jest reprezentowana jako x [n].
Do testowania systemu stosuje się zwykle sygnały standardowe lub podstawowe. Sygnały te są podstawowymi elementami budulcowymi wielu złożonych sygnałów. Dlatego odgrywają bardzo ważną rolę w badaniu sygnałów i systemów.
Jednostkowy impuls lub funkcja delta
Sygnał spełniający warunek, $\delta(t) = \lim_{\epsilon \to \infty} x(t)$nazywany jest jednostkowym sygnałem impulsowym. Sygnał ten dąży do nieskończoności, gdy t = 0 i dąży do zera, gdy t ≠ 0, tak że obszar pod jego krzywą jest zawsze równy jeden. Funkcja delta ma wszędzie zerową amplitudę excunit_impulse.jpgept przy t = 0.

Właściwości jednostkowego sygnału impulsowego
- δ (t) jest sygnałem parzystym.
- δ (t) nie jest przykładem sygnału ani energii, ani mocy (NENP).
- Obszar jednostkowego sygnału impulsowego można zapisać jako; $$A = \int_{-\infty}^{\infty} \delta (t)dt = \int_{-\infty}^{\infty} \lim_{\epsilon \to 0} x(t) dt = \lim_{\epsilon \to 0} \int_{-\infty}^{\infty} [x(t)dt] = 1$$
- Wagę lub siłę sygnału można zapisać jako; $$y(t) = A\delta (t)$$
- Obszar ważonego sygnału impulsowego można zapisać jako - $$y (t) = \int_{-\infty}^{\infty} y (t)dt = \int_{-\infty}^{\infty} A\delta (t) = A[\int_{-\infty}^{\infty} \delta (t)dt ] = A = 1 = Wigthedimpulse$$
Sygnał kroku jednostki
Sygnał, który spełnia dwa następujące warunki -
- $U(t) = 1(when\quad t \geq 0 )and$
- $U(t) = 0 (when\quad t < 0 )$
jest znany jako sygnał kroku jednostkowego.
Ma właściwość wykazywania nieciągłości przy t = 0. W punkcie nieciągłości wartość sygnału jest podana jako średnia wartości sygnału. Sygnał ten został pobrany tuż przed i po punkcie nieciągłości (według Zjawisk Gibba).
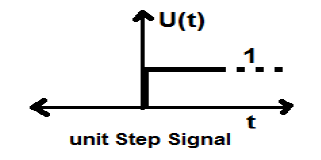
Jeśli dodamy sygnał kroku do innego sygnału kroku, który jest skalowany w czasie, wynikiem będzie jedność. Jest to sygnał typu mocy, a wartość mocy wynosi 0,5. Wartość RMS (Root mean square) wynosi 0,707, a jej średnia wartość również wynosi 0,5
Sygnał rampy
Całkowanie sygnału kroku daje w wyniku sygnał Ramp. Jest reprezentowany przez r (t). Sygnał rampy również spełnia warunek$r(t) = \int_{-\infty}^{t} U(t)dt = tU(t)$. Nie jest to sygnał typu energii ani mocy (NENP).
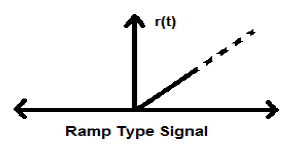
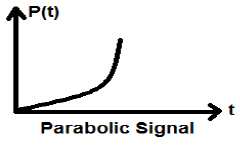
Sygnał paraboliczny
Całkowanie sygnału Ramp prowadzi do sygnału parabolicznego. Jest reprezentowany przez p (t). Warunek spełnia również sygnał paraboliczny$p(t) = \int_{-\infty}^{t} r(t)dt = (t^{2}/2)U(t)$. Nie jest to sygnał typu energii ani mocy (NENP).
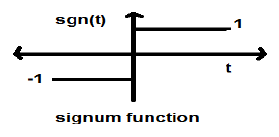
Funkcja Signum
Ta funkcja jest reprezentowana jako
$$sgn(t) = \begin{cases}1 & for\quad t >0\\-1 & for\quad t<0\end{cases}$$Jest to sygnał typu mocy. Jego wartość mocy i wartości RMS (średnia kwadratowa) wynoszą 1. Średnia wartość funkcji signum wynosi zero.
Funkcja Sinc
Jest to również funkcja sinusa i jest zapisywane jako -
$$SinC(t) = \frac{Sin\Pi t}{\Pi T} = Sa(\Pi t)$$Właściwości funkcji Sinc
Jest to sygnał typu energetycznego.
$Sinc(0) = \lim_{t \to 0}\frac{\sin \Pi t}{\Pi t} = 1$
$Sinc(\infty) = \lim_{t \to \infty}\frac{\sin \Pi \infty}{\Pi \infty} = 0$ (Zakres sinπ∞ waha się od -1 do +1, ale wszystko podzielone przez nieskończoność jest równe zero)
-
Gdyby $ \sin c(t) = 0 => \sin \Pi t = 0$
$\Rightarrow \Pi t = n\Pi$
$\Rightarrow t = n (n \neq 0)$
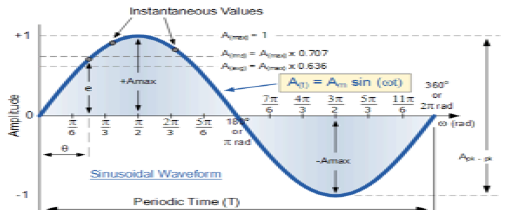
Sygnał sinusoidalny
Sygnał o charakterze ciągłym nazywany jest sygnałem ciągłym. Ogólny format sygnału sinusoidalnego to
$$x(t) = A\sin (\omega t + \phi )$$Tutaj,
A = amplituda sygnału
ω = częstotliwość kątowa sygnału (mierzona w radianach)
φ = kąt fazowy sygnału (mierzony w radianach)
Ten sygnał ma tendencję do powtarzania się po pewnym czasie, dlatego nazywany jest sygnałem okresowym. Okres czasu sygnału jest podany jako;
$$T = \frac{2\pi }{\omega }$$Schematyczny widok sygnału sinusoidalnego pokazano poniżej.
Funkcja prostokątna
Mówi się, że sygnał jest prostokątnym typem funkcji, jeśli spełnia następujący warunek -
$$\pi(\frac{t}{\tau}) = \begin{cases}1, & for\quad t\leq \frac{\tau}{2}\\0, & Otherwise\end{cases}$$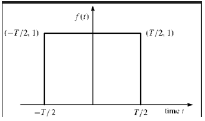
Ponieważ sygnał ten jest symetryczny względem osi Y, nazywany jest sygnałem parzystym.
Trójkątny sygnał impulsowy
Każdy sygnał, który spełnia następujący warunek, nazywany jest sygnałem trójkątnym.
$$\Delta(\frac{t}{\tau}) = \begin{cases}1-(\frac{2|t|}{\tau}) & for|t|<\frac{\tau}{2}\\0 & for|t|>\frac{\tau}{2}\end{cases}$$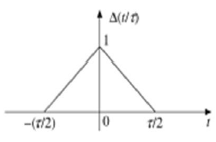
Ten sygnał jest symetryczny względem osi Y. Dlatego jest również określany jako sygnał równy.
Widzieliśmy, jak można przedstawić podstawowe sygnały w dziedzinie czasu ciągłego. Zobaczmy, jak podstawowe sygnały mogą być reprezentowane w dziedzinie czasu dyskretnego.
Sekwencja impulsów jednostkowych
Jest oznaczony jako δ (n) w dyskretnej dziedzinie czasu i można go zdefiniować jako;
$$\delta(n)=\begin{cases}1, & for \quad n=0\\0, & Otherwise\end{cases}$$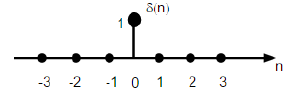
Sygnał kroku jednostki
Dyskretny sygnał kroku jednostki czasu jest zdefiniowany jako;
$$U(n)=\begin{cases}1, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$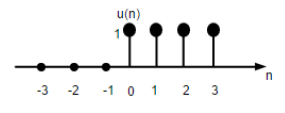
Powyższy rysunek przedstawia graficzną reprezentację dyskretnej funkcji kroku.
Funkcja rampy jednostki
Funkcję rampy jednostkowej dyskretnej można zdefiniować jako -
$$r(n)=\begin{cases}n, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$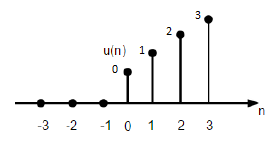
Rysunek podany powyżej przedstawia graficzną reprezentację dyskretnego sygnału rampy.
Funkcja paraboliczna
Funkcja paraboliczna jednostki dyskretnej jest oznaczona jako p (n) i może być zdefiniowana jako;
$$p(n) = \begin{cases}\frac{n^{2}}{2} ,& for \quad n\geq0\\0, & for \quad n<0\end{cases}$$Pod względem funkcji kroku jednostkowego można go zapisać jako;
$$P(n) = \frac{n^{2}}{2}U(n)$$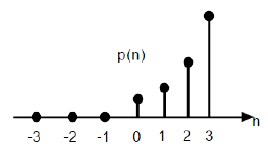
Powyższy rysunek przedstawia graficzną reprezentację sekwencji parabolicznej.
Sygnał sinusoidalny
Wszystkie sygnały ciągłe są okresowe. Sekwencje sinusoidalne w czasie dyskretnym mogą być okresowe lub nie. Zależą od wartości ω. Aby dyskretny sygnał czasu był okresowy, częstotliwość kątowa ω musi być wymierną wielokrotnością 2π.
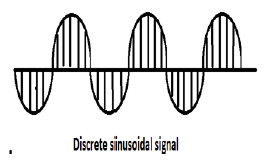
Na powyższym rysunku pokazano dyskretny sygnał sinusoidalny.
Dyskretną postać sygnału sinusoidalnego można przedstawić w formacie -
$$x(n) = A\sin(\omega n + \phi)$$Tutaj A, ω i φ mają swoje zwykłe znaczenie, a n jest liczbą całkowitą. Okres czasu dyskretnego sygnału sinusoidalnego jest określony wzorem -
$$N =\frac{2\pi m}{\omega}$$Gdzie, N i m są liczbami całkowitymi.
Ciągłe sygnały czasu można sklasyfikować według różnych warunków lub operacji wykonywanych na sygnałach.
Sygnały parzyste i nieparzyste
Nawet sygnał
Mówi się, że sygnał jest, nawet jeśli spełnia następujący warunek;
$$x(-t) = x(t)$$Odwrócenie czasu sygnału nie implikuje tutaj żadnej zmiany amplitudy. Weźmy na przykład pod uwagę trójkątną falę pokazaną poniżej.
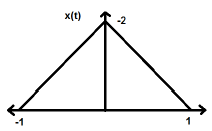
Sygnał trójkątny jest sygnałem parzystym. Ponieważ jest symetryczny względem osi Y. Można powiedzieć, że jest to odbicie lustrzane wokół osi Y.
Rozważ inny sygnał, jak pokazano na poniższym rysunku.
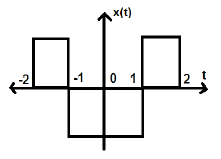
Widzimy, że powyższy sygnał jest symetryczny względem osi Y.
Dziwny sygnał
Mówi się, że sygnał jest dziwny, jeśli spełnia następujący warunek
$$x(-t) = -x(t)$$Tutaj odwrócenie czasu i zmiana amplitudy zachodzą jednocześnie.
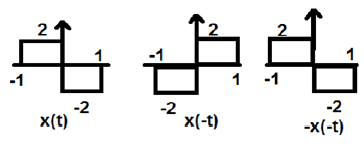
Na powyższym rysunku widzimy sygnał kroku x (t). Aby sprawdzić, czy jest to sygnał nieparzysty, czy nie, najpierw wykonujemy odwrócenie czasu, tj. X (-t), a wynik jest taki, jak pokazano na rysunku. Następnie odwracamy amplitudę sygnału wypadkowego tj. –X (-t) i otrzymujemy wynik jak na rysunku.
Jeśli porównamy pierwszy i trzeci przebieg, zobaczymy, że są one takie same, tj. X (t) = -x (-t), co spełnia nasze kryteria. Dlatego powyższy sygnał jest sygnałem Odd.
Poniżej przedstawiono kilka ważnych wyników związanych z sygnałami parzystymi i nieparzystymi.
- Parzyste × Parzyste = Parzyste
- Nieparzyste × Nieparzyste = Parzyste
- Parzyste × Nieparzyste = Nieparzyste
- Parzysty ± Parzysty = Parzysty
- Nieparzyste ± Nieparzyste = Nieparzyste
- Parzyste ± Nieparzyste = Ani parzyste, ani nieparzyste
Reprezentacja dowolnego sygnału w formie parzystej lub nieparzystej
Niektórych sygnałów nie można bezpośrednio sklasyfikować jako parzyste lub nieparzyste. Są one reprezentowane jako połączenie parzystego i nieparzystego sygnału.
$$x(t)\rightarrow x_{e}(t)+x_{0}(t)$$Gdzie x e (t) reprezentuje sygnał parzysty, a x o (t) reprezentuje sygnał nieparzysty
$$x_{e}(t)=\frac{[x(t)+x(-t)]}{2}$$I
$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$Przykład
Znajdź parzyste i nieparzyste części sygnału $x(n) = t+t^{2}+t^{3}$
Solution - Z odwrócenia x (n) otrzymujemy
$$x(-n) = -t+t^{2}-t^{3}$$
Teraz, zgodnie ze wzorem, część parzysta
$$x_{e}(t) = \frac{x(t)+x(-t)}{2}$$
$$= \frac{[(t+t^{2}+t^{3})+(-t+t^{2}-t^{3})]}{2}$$
$$= t^{2}$$
Podobnie, zgodnie ze wzorem, część nieparzysta jest
$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$
$$= \frac{[(t+t^{2}+t^{3})-(-t+t^{2}-t^{3})]}{2}$$
$$= t+t^{3}$$
Sygnały okresowe i nieokresowe
Sygnały okresowe
Okresowy sygnał powtarza się po pewnym czasie. Możemy to pokazać w formie równania jako -
$$x(t) = x(t)\pm nT$$Gdzie, n = liczba całkowita (1,2,3 ……)
T = podstawowy okres czasu (FTP) ≠ 0 i ≠ ∞
Podstawowy okres czasu (FTP) to najmniejsza dodatnia i stała wartość czasu, dla którego sygnał jest okresowy.
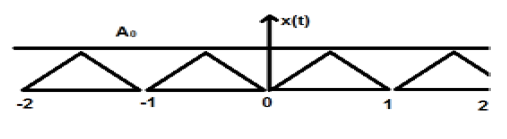
Na powyższym rysunku przedstawiono trójkątny sygnał o amplitudzie A. Tutaj sygnał powtarza się co 1 sek. Dlatego można powiedzieć, że sygnał jest okresowy, a jego współczynnik FTP wynosi 1 sek.
Sygnał nieokresowy
Można po prostu powiedzieć, że sygnały, które nie są okresowe, mają charakter nieokresowy. Jak oczywiste, sygnały te nie będą się powtarzać po jakimkolwiek czasie.
Sygnały nieokresowe nie mają określonego formatu; dlatego żadne konkretne równanie matematyczne nie może ich opisać.
Sygnały energii i mocy
Mówi się, że sygnał jest sygnałem energii, wtedy i tylko wtedy, gdy całkowita zawarta w nim energia jest skończona i niezerowa (0 <E <∞). Dlatego dla dowolnego sygnału typu energii całkowity znormalizowany sygnał jest skończony i niezerowy.
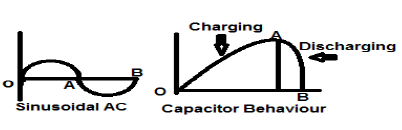
Sinusoidalny sygnał prądu przemiennego jest doskonałym przykładem sygnału typu Energia, ponieważ w jednym przypadku jest w dodatnim półcyklu, a następnie jest ujemny w następnym półcyklu. Dlatego jego średnia moc wynosi zero.
Bezstratny kondensator jest również doskonałym przykładem sygnału typu Energy, ponieważ po podłączeniu do źródła ładuje się do optymalnego poziomu, a po usunięciu źródła rozprasza tę równą ilość energii przez obciążenie i sprawia, że jego średnia moc zero.
Dla każdego skończonego sygnału x (t) energia może być symbolizowana jako E i zapisywana jako;
$$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$Gęstość widmowa sygnałów typu energii określa ilość energii rozprowadzanej na różnych poziomach częstotliwości.
Sygnały typu mocy
O sygnale mówi się, że jest sygnałem typu mocy, wtedy i tylko wtedy, gdy znormalizowana moc średnia jest skończona i niezerowa, tj. (0 <p <∞). Dla sygnału typu mocy znormalizowana średnia moc jest skończona i niezerowa. Prawie wszystkie sygnały okresowe są sygnałami mocy, a ich średnia moc jest skończona i niezerowa.
W formie matematycznej moc sygnału x (t) można zapisać jako;
$$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$Różnica między sygnałami energii i mocy
Poniższa tabela podsumowuje różnice sygnałów energii i mocy.
| Sygnał mocy | Sygnał energii |
|---|---|
| Praktyczne sygnały okresowe to sygnały mocy. | Sygnały nieokresowe to sygnały energii. |
| Tutaj znormalizowana średnia moc jest skończona i niezerowa. | Tutaj całkowita znormalizowana energia jest skończona i niezerowa. |
| Matematycznie, $$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$ |
Matematycznie, $$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$ |
| Istnienie tych sygnałów jest nieskończone w czasie. | Sygnały te istnieją przez ograniczony czas. |
| Energia sygnału mocy jest nieskończona w nieskończonym czasie. | Moc sygnału energetycznego wynosi zero w nieskończonym czasie. |
Rozwiązane przykłady
Example 1 - Znajdź moc sygnału $z(t) = 2\cos(3\Pi t+30^{o})+4\sin(3\Pi +30^{o})$
Solution- Powyższe dwa sygnały są względem siebie ortogonalne, ponieważ ich składniki częstotliwościowe są identyczne, a także mają taką samą różnicę faz. Zatem całkowita moc będzie sumą indywidualnych mocy.
Pozwolić $z(t) = x(t)+y(t)$
Gdzie $x(t) = 2\cos (3\Pi t+30^{o})$ i $y(t) = 4\sin(3\Pi +30^{o})$
Moc $x(t) = \frac{2^{2}}{2} = 2$
Moc $y(t) = \frac{4^{2}}{2} = 8$
W związku z tym, $P(z) = p(x)+p(y) = 2+8 = 10$… Ans.
Example 2 - Sprawdź, czy podany sygnał $x(t) = t^{2}+j\sin t$ jest koniugatem czy nie?
Solution- Tutaj część rzeczywista będąca t 2 jest częścią parzystą i nieparzystą (urojoną)$\sin t$to jest dziwne. Zatem powyższy sygnał jest sygnałem sprzężonym.
Example 3 - Sprawdź, czy $X(t)= \sin \omega t$ jest sygnałem nieparzystym lub parzystym.
Solution - Biorąc $X(t) = \sin \omega t$
Otrzymamy do odwrócenia czasu $\sin (-\omega t)$
Ale my to wiemy $\sin(-\phi) = -\sin \phi$.
W związku z tym,
$$\sin (-\omega t) = -\sin \omega t$$To spełnia warunek, aby sygnał był nieparzysty. W związku z tym,$\sin \omega t$ to dziwny sygnał.
Podobnie jak ciągłe sygnały czasu, dyskretne sygnały czasu mogą być klasyfikowane według warunków lub operacji na sygnałach.
Sygnały parzyste i nieparzyste
Nawet sygnał
Mówi się, że sygnał jest parzysty lub symetryczny, jeśli spełnia następujący warunek;
$$x(-n) = x(n)$$
Tutaj widzimy, że x (-1) = x (1), x (-2) = x (2) i x (-n) = x (n). Jest to więc równy sygnał.
Dziwny sygnał
Mówi się, że sygnał jest dziwny, jeśli spełnia następujący warunek;
$$x(-n) = -x(n)$$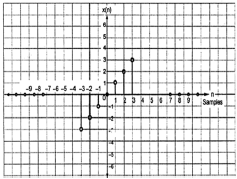
Na rysunku widzimy, że x (1) = -x (-1), x (2) = -x (2) i x (n) = -x (-n). W związku z tym jest to dziwny, a także anty-symetryczny sygnał.
Sygnały okresowe i nieokresowe
Dyskretny sygnał czasowy jest okresowy wtedy i tylko wtedy, gdy spełnia następujący warunek -
$$x(n+N) = x(n)$$Tutaj sygnał x (n) powtarza się po N okresie. Można to najlepiej zrozumieć, rozważając sygnał cosinusowy -
$$x(n) = A \cos(2\pi f_{0}n+\theta)$$ $$x(n+N) = A\cos(2\pi f_{0}(n+N)+\theta) = A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$ $$= A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$Aby sygnał stał się okresowy, należy spełnić następujący warunek;
$$x(n+N) = x(n)$$ $$\Rightarrow A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta) = A \cos(2\pi f_{0}n+\theta)$$to znaczy $2\pi f_{0}N$ jest całkowitą wielokrotnością $2\pi$
$$2\pi f_{0}N = 2\pi K$$ $$\Rightarrow N = \frac{K}{f_{0}}$$Częstotliwości dyskretnych sygnałów sinusoidalnych są oddzielone całkowitą wielokrotnością $2\pi$.
Sygnały energii i mocy
Sygnał energii
Energię dyskretnego sygnału czasu oznaczamy jako E. Matematycznie można ją zapisać jako;
$$E = \displaystyle \sum\limits_{n=-\infty}^{+\infty}|x(n)|^2$$Jeśli poszczególne wartości $x(n)$są podnoszone do kwadratu i dodawane, otrzymujemy sygnał energii. Tutaj$x(n)$ jest sygnałem energii, a jego energia jest skończona w czasie, tj. 0 $ <E <\ infty $
Sygnał mocy
Średnia moc sygnału dyskretnego jest reprezentowana jako P. Matematycznie można to zapisać jako;
$$P = \lim_{N \to \infty} \frac{1}{2N+1}\displaystyle\sum\limits_{n=-N}^{+N} |x(n)|^2$$Tutaj moc jest skończona, tj. 0 <P <∞. Istnieją jednak sygnały, które nie należą ani do sygnału typu energii, ani mocy.
Istnieją inne sygnały, które są wynikiem wykonanej na nich operacji. Poniżej omówiono niektóre popularne typy sygnałów.
Sygnały sprzężone
Sygnały, które spełniają warunek $x(t) = x*(-t)$ nazywane są sygnałami sprzężonymi.
Pozwolić $x(t) = a(t)+jb(t)$... eqn. 1
Więc, $x(-t) = a(-t)+jb(-t)$
I $x*(-t) = a(-t)-jb(-t)$... eqn. 2
Według stanu, $x(t) = x*(-t)$
Jeśli porównamy oba wyprowadzone równania 1 i 2, zobaczymy, że część rzeczywista jest parzysta, podczas gdy część urojona jest nieparzysta. Jest to warunek, aby sygnał był typem sprzężonym.
Sprzężone sygnały anty-symetryczne
Sygnały, które spełniają warunek $x(t) = -x*(-t)$ nazywane są sprzężonym sygnałem anty-symetrycznym
Pozwolić $x(t) = a(t)+jb(t)$... eqn. 1
Więc $x(-t) = a(-t)+jb(-t)$
I $x*(-t) = a(-t)-jb(-t)$
$-x*(-t) = -a(-t)+jb(-t)$... eqn. 2
Według stanu $x(t) = -x*(-t)$
Teraz jeszcze raz porównaj oba równania, tak jak zrobiliśmy to dla sygnałów sprzężonych. Tutaj stwierdzimy, że część rzeczywista jest nieparzysta, a część urojona parzysta. Jest to warunek, aby sygnał stał się sprzężonym typem anty-symetrycznym.
Przykład
Niech będzie dany sygnał $x(t) = \sin t+jt^{2}$.
Tutaj, prawdziwa część jest $\sin t$ jest dziwne, a część urojona jest $t^2$jest równa. Zatem sygnał ten można sklasyfikować jako sprzężony sygnał antysymetryczny.
Dowolną funkcję można podzielić na dwie części. Jedna część to sprzężona symetria, a druga część jest sprzężona anty-symetryczna. Zatem każdy sygnał x (t) można zapisać jako
$$x(t) = xcs(t)+xcas(t)$$Gdzie $xcs(t)$ jest sprzężonym sygnałem symetrycznym i $xcas(t)$ jest sprzężonym sygnałem antysymetrycznym
$$xcs(t) = \frac{[x(t)+x*(-t)]}{2}$$I
$$xcas(t) = \frac{[x(t)-x*(-t)]}{2}$$Sygnały symetryczne półfalowe
Gdy sygnał spełnia warunek $cx(t) = -x(t\pm (\frac{T_{0}}{2}))$nazywa się to symetrycznym sygnałem półfalowym. Tutaj odwrócenie amplitudy i przesunięcie czasu sygnału następuje o połowę. Dla symetrycznego sygnału półfalowego średnia wartość będzie wynosić zero, ale nie ma to miejsca, gdy sytuacja jest odwrotna.
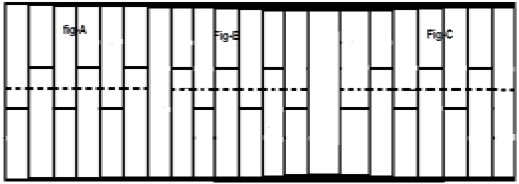
Rozważmy sygnał x (t), jak pokazano na rysunku A powyżej. Pierwszym krokiem jest przesunięcie sygnału w czasie i uczynienie go$x[t-(\frac{T}{2})]$. Zatem nowy sygnał jest zmieniany, jak pokazano na rysunku B. Następnie odwracamy amplitudę sygnału, czyli robimy go$-x[t-(\frac{T}{2})]$ jak pokazano na rysunku C. Ponieważ sygnał ten powtarza się po półokresowym przesunięciu i odwróceniu amplitudy, jest to symetryczny sygnał półfalowy.
Sygnał ortogonalny
O dwóch sygnałach x (t) i y (t) mówi się, że są ortogonalne, jeśli spełniają dwa następujące warunki.
Condition 1 - $\int_{-\infty}^{\infty}x(t)y(t) = 0$ [dla sygnału nieokresowego]
Condition 2 - $\int x(t)y(t) = 0$ [Dla sygnału okresowego]
Sygnały, które zawierają składowe harmoniczne (3 rd , 5 th , 7 th ... itd.) I mają różne częstotliwości, wzajemnie do siebie prostopadłe.
W sygnałach typu trygonometrycznego funkcje sinus i cosinus są również ortogonalne względem siebie; pod warunkiem, że mają tę samą częstotliwość i są w tej samej fazie. W ten sam sposób DC (sygnały prądu stałego) i sygnały sinusoidalne są również ortogonalne względem siebie. Jeśli x (t) i y (t) to dwa sygnały ortogonalne i$z(t) = x(t)+y(t)$ wtedy moc i energię z (t) można zapisać jako;
$$P(z) = p(x)+p(y)$$ $$E(z) = E(x)+E(y)$$Przykład
Przeanalizuj sygnał: $z(t) = 3+4\sin(2\pi t+30^0)$
Tutaj sygnał składa się z sygnału DC (3) i jednej funkcji sinusoidalnej. Tak więc, zgodnie z właściwością, ten sygnał jest sygnałem ortogonalnym, a dwa zawarte w nim pod-sygnały są wzajemnie ortogonalne.
Przesunięcie oznacza ruch sygnału w dziedzinie czasu (wokół osi Y) lub w dziedzinie amplitudy (wokół osi X). Odpowiednio, możemy podzielić przesunięcie na dwie kategorie nazwane jako Przesunięcie w czasie i Przesunięcie amplitudy, które są następnie omówione poniżej.
Przesunięcie w czasie
Przesunięcie czasu oznacza przesunięcie sygnałów w dziedzinie czasu. Matematycznie można to zapisać jako
$$x(t) \rightarrow y(t+k)$$Ta wartość K może być dodatnia lub ujemna. Zgodnie ze znakiem wartości k mamy dwa rodzaje przesunięć nazwane jako Przesunięcie w prawo i Przesunięcie w lewo.
Przypadek 1 (K> 0)
Gdy K jest większe od zera, przesunięcie sygnału następuje w kierunku „w lewo” w dziedzinie czasu. Dlatego ten rodzaj przesuwania jest znany jako lewe przesunięcie sygnału.
Example
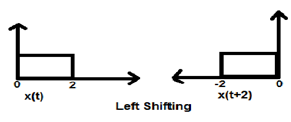
Przypadek 2 (K <0)
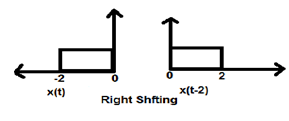
Gdy K jest mniejsze od zera, przesunięcie sygnału następuje w prawo w dziedzinie czasu. Dlatego ten rodzaj przesunięcia jest znany jako przesunięcie w prawo.
Example
Poniższy rysunek przedstawia przesunięcie sygnału w prawo o 2.
Przesunięcie amplitudy
Przesunięcie amplitudy oznacza przesunięcie sygnału w domenie amplitudy (wokół osi X). Matematycznie można to przedstawić jako -
$$x(t) \rightarrow x(t)+K$$Ta wartość K może być dodatnia lub ujemna. W związku z tym mamy dwa rodzaje przesunięcia amplitudy, które zostaną następnie omówione poniżej.
Przypadek 1 (K> 0)
Kiedy K jest większe od zera, następuje przesunięcie sygnału w górę na osi X. Dlatego ten rodzaj przesunięcia jest znany jako przesunięcie w górę.
Example
Rozważmy sygnał x (t), który jest dany jako;
$$x = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$Weźmy K = + 1, aby nowy sygnał można zapisać jako -
$y(t) \rightarrow x(t)+1$ Zatem y (t) można ostatecznie zapisać jako;
$$x(t) = \begin{cases}1, & t < 0\\2, & 0\leq t\leq 2\\ 1, & t>0\end{cases}$$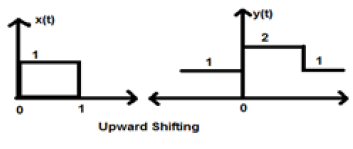
Przypadek 2 (K <0)
Gdy K jest mniejsze od zera, następuje przesunięcie sygnału w dół na osi X. Dlatego nazywa się to przesunięciem sygnału w dół.
Example
Rozważmy sygnał x (t), który jest dany jako;
$$x(t) = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$Przyjmijmy K = -1, aby nowy sygnał można zapisać jako;
$y(t)\rightarrow x(t)-1$ Zatem y (t) można ostatecznie zapisać jako;
$$y(t) = \begin{cases}-1, & t < 0\\0, & 0\leq t\leq 2\\ -1, & t>0\end{cases}$$
Skalowanie sygnału oznacza, że stała jest mnożona przez czas lub amplitudę sygnału.
Skalowanie czasu
Jeśli stała jest pomnożona do osi czasu, wtedy nazywa się to skalowaniem czasu. Można to matematycznie przedstawić jako;
$x(t) \rightarrow y(t) = x(\alpha t)$ lub $x(\frac{t}{\alpha})$; gdzie α ≠ 0
Zatem oś y jest taka sama, wielkość osi x maleje lub rośnie zgodnie ze znakiem stałej (dodatniej lub ujemnej). Dlatego skalowanie można również podzielić na dwie kategorie, jak omówiono poniżej.
Kompresja czasu
Zawsze, gdy wartość alfa jest większa od zera, amplituda sygnału jest dzielona przez wartość alfa, podczas gdy wartość na osi Y pozostaje taka sama. Jest to znane jako kompresja czasu.
Example
Rozważmy sygnał x (t), który pokazano na poniższym rysunku. Przyjmijmy wartość alfa jako 2. Zatem y (t) będzie równe x (2t), co ilustruje podany rysunek.

Wyraźnie widać na powyższych rysunkach, że wielkość czasu na osi y pozostaje taka sama, ale amplituda na osi x zmniejsza się z 4 do 2. Jest to zatem przypadek kompresji czasu.
Rozszerzenie czasu
Gdy czas jest podzielony przez stałą wartość alfa, amplituda sygnału na osi Y zostaje pomnożona przez współczynnik alfa, co pozwala zachować wielkość osi X w niezmienionej postaci. Dlatego nazywa się to sygnałem typu rozszerzenie czasu.
Example
Rozważmy kwadratowy sygnał x (t) o wielkości 1. Kiedy przeskalujemy go w czasie o stałą 3, tak że $x(t) \rightarrow y(t) \rightarrow x(\frac{t}{3})$, następnie amplituda sygnału jest modyfikowana 3 razy, co pokazano na poniższym rysunku.
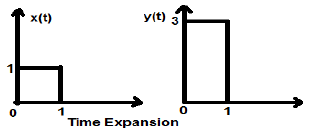
Skalowanie amplitudy
Mnożenie stałej przez amplitudę sygnału powoduje skalowanie amplitudy. W zależności od znaku stałej może to być skalowanie amplitudy lub tłumienie. Rozważmy sygnał prostokątny x (t) = Π (t / 4).
Załóżmy, że definiujemy inną funkcję y (t) = 2 Π (t / 4). W takim przypadku wartość osi y zostanie podwojona, zachowując wartość osi czasu bez zmian. Ilustruje to poniższy rysunek.
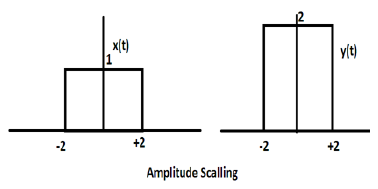
Rozważmy inną funkcję prostokątną zdefiniowaną jako z (t), gdzie z (t) = 0,5 Π (t / 4). Tutaj amplituda funkcji z (t) będzie równa połowie amplitudy x (t), tj. Oś czasu pozostanie taka sama, oś amplitudy zostanie zmniejszona o połowę. Ilustruje to poniższy rysunek.
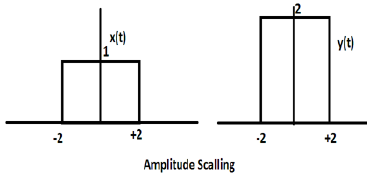
Ilekroć czas w sygnale zostanie pomnożony przez -1, sygnał zostanie odwrócony. Tworzy swoje lustrzane odbicie wokół osi Y lub X. Nazywa się to odwróceniem sygnału.
Odwrócenie można podzielić na dwa typy na podstawie warunku, czy czas lub amplituda sygnału jest pomnożona przez -1.
Odwrócenie czasu
Ilekroć czas sygnału jest pomnożony przez -1, jest to znane jako odwrócenie czasu sygnału. W tym przypadku sygnał wytwarza swoje lustrzane odbicie wokół osi Y. Matematycznie można to zapisać jako;
$$x(t) \rightarrow y(t) \rightarrow x(-t)$$Najlepiej można to zrozumieć na poniższym przykładzie.

W powyższym przykładzie możemy wyraźnie zobaczyć, że sygnał został odwrócony wokół jego osi Y. Jest to więc również jeden rodzaj skalowania czasu, ale tutaj wielkość skalowania wynosi zawsze (-1).
Odwrócenie amplitudy
Ilekroć amplituda sygnału jest pomnożona przez -1, nazywa się to odwróceniem amplitudy. W tym przypadku sygnał wytwarza swoje lustrzane odbicie wokół osi X. Matematycznie można to zapisać jako;
$$x(t)\rightarrow y(t)\rightarrow -x(t)$$Rozważmy następujący przykład. Wyraźnie widać odwrócenie amplitudy.
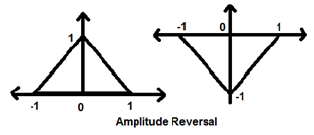
Dwie bardzo ważne operacje wykonywane na sygnałach to Różnicowanie i Całkowanie.
Różnicowanie
Różnicowanie dowolnego sygnału x (t) oznacza reprezentację nachylenia tego sygnału w odniesieniu do czasu. Matematycznie jest reprezentowany jako;
$$x(t)\rightarrow \frac{dx(t)}{dt}$$W przypadku różnicowania OPAMP ta metodologia jest bardzo pomocna. Sygnał można łatwo odróżnić graficznie, zamiast używać wzoru. Warunkiem jest jednak to, że sygnał musi być prostokątny lub trójkątny, co zdarza się w większości przypadków.
| Oryginalny sygnał | Sygnał zróżnicowany |
|---|---|
| Rampa | Krok |
| Krok | Impuls |
| Impuls | 1 |
Powyższa tabela ilustruje stan sygnału po zróżnicowaniu. Na przykład sygnał rampowy po zróżnicowaniu przekształca się w sygnał krokowy. Podobnie, jednostkowy sygnał kroku staje się sygnałem impulsowym.
Przykład
Niech będzie dany nam sygnał $x(t) = 4[r(t)-r(t-2)]$. Gdy ten sygnał zostanie wykreślony, będzie wyglądał jak ten po lewej stronie rysunku podanego poniżej. Teraz naszym celem jest różnicowanie danego sygnału.
Na początek zaczniemy różnicować podane równanie. Wiemy, że sygnał rampy po różniczkowaniu daje sygnał kroku jednostkowego.
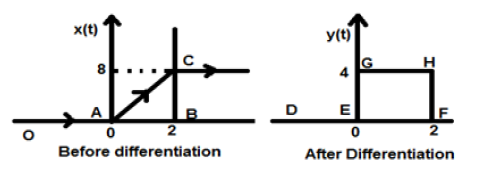
Zatem nasz wynikowy sygnał y (t) można zapisać jako;
$y(t) = \frac{dx(t)}{dt}$
$= \frac{d4[r(t)-r(t-2)]}{dt}$
$= 4[u(t)-u(t-2)]$
Teraz ten sygnał jest ostatecznie wykreślany, co pokazano po prawej stronie powyższego rysunku.
Całkowanie dowolnego sygnału oznacza sumowanie tego sygnału w określonej dziedzinie czasu w celu uzyskania zmodyfikowanego sygnału. Matematycznie można to przedstawić jako -
$$x(t)\rightarrow y(t) = \int_{-\infty}^{t}x(t)dt$$Tutaj również w większości przypadków możemy przeprowadzić całkowanie matematyczne i znaleźć wynikowy sygnał, ale bezpośrednia integracja w krótkich odstępach czasu jest możliwa dla sygnałów, które są przedstawione graficznie w formacie prostokątnym. Podobnie jak w przypadku różnicowania, tutaj również odwołamy się do tabeli, aby szybko uzyskać wynik.
| Oryginalny sygnał | Zintegrowany sygnał |
|---|---|
| 1 | impuls |
| Impuls | krok |
| Krok | Rampa |
Przykład
Rozważmy sygnał $x(t) = u(t)-u(t-3)$. Przedstawiono to na rys. 1 poniżej. Najwyraźniej widzimy, że jest to sygnał kroku. Teraz zintegrujemy to. Odnosząc się do tabeli wiemy, że całkowanie sygnału kroku daje sygnał rampy.
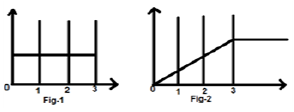
Jednak obliczymy to matematycznie,
$y(t) = \int_{-\infty}^{t}x(t)dt$
$= \int_{-\infty}^{t}[u(t)-u(t-3)]dt$
$= \int_{-\infty}^{t}u(t)dt-\int_{-\infty}^{t}u(t-3)dt$
$= r(t)-r(t-3)$
To samo jest wykreślane, jak pokazano na rys. 2,
Splot dwóch sygnałów w dziedzinie czasu jest równoznaczny z pomnożeniem ich reprezentacji w dziedzinie częstotliwości. Matematycznie możemy zapisać splot dwóch sygnałów jako
$$y(t) = x_{1}(t)*x_{2}(t)$$ $$= \int_{-\infty}^{\infty}x_{1}(p).x_{2}(t-p)dp$$Kroki do splotu
- Weź sygnał x 1 (t) i umieść tam t = p, aby było x 1 (p).
- Weź sygnał x 2 (t) i wykonaj krok 1 i zrób to x 2 (p).
- Zrób zwijanie sygnału, tj. X 2 (-p).
- Dokonaj przesunięcia w czasie powyższego sygnału x 2 [- (pt)]
- Następnie pomnóż oba sygnały. to znaczy$x_{1}(p).x_{2}[−(p−t)]$
Przykład
Zróbmy splot sygnału krokowego u (t) z jego własnym rodzajem.
$y(t) = u(t)*u(t)$
$= \int_{-\infty}^{\infty}[u(p).u[-(p-t)]dp$
Teraz to t może być większe lub mniejsze od zera, co pokazano na poniższych rysunkach
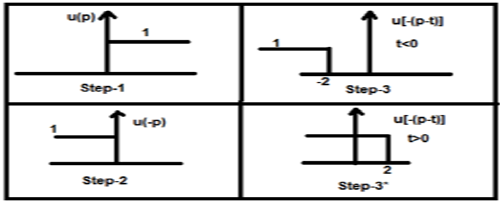
Tak więc w powyższym przypadku wynik powstaje z następującymi możliwościami
$y(t) = \begin{cases}0, & if\quad t<0\\\int_{0}^{t}1dt, & for\quad t>0\end{cases}$
$= \begin{cases}0, & if\quad t<0\\t, & t>0\end{cases} = r(t)$
Właściwości splotu
Przemienne
Stwierdza, że kolejność splotów nie ma znaczenia, co można przedstawić matematycznie jako
$$x_{1}(t)*x_{2}(t) = x_{2}(t)*x_{1}(t)$$Asocjacyjny
Stwierdza, że kolejność splotów obejmująca trzy sygnały może być dowolna. Matematycznie można to pokazać jako;
$$x_{1}(t)*[x_{2}(t)*x_{3}(t)] = [x_{1}(t)*x_{2}(t)]*x_{3}(t)$$Dystrybucyjny
Najpierw można dodać dwa sygnały, a następnie wprowadzić ich splot do trzeciego sygnału. Jest to równoważne splotowi dwóch sygnałów indywidualnie z trzecim sygnałem i ostatecznie dodanym. Matematycznie można to zapisać jako;
$$x_{1}(t)*[x_{2}(t)+x_{3}(t)] = [x_{1}(t)*x_{2}(t)+x_{1}(t)*x_{3}(t)]$$Powierzchnia
Jeżeli sygnał jest wynikiem splotu dwóch sygnałów, wówczas obszar sygnału jest zwielokrotnieniem tych pojedynczych sygnałów. Matematycznie można to zapisać
Gdyby $y(t) = x_{1}*x_{2}(t)$
Wtedy obszar y (t) = obszar x 1 (t) X obszar x 2 (t)
skalowanie
Jeśli dwa sygnały zostaną przeskalowane do jakiejś nieznanej stałej „a”, a splot zostanie wykonany, wynikowy sygnał również zostanie spleciony na tę samą stałą „a” i zostanie podzielony przez tę wielkość, jak pokazano poniżej.
Gdyby, $x_{1}(t)*x_{2}(t) = y(t)$
Następnie, $x_{1}(at)*x_{2}(at) = \frac{y(at)}{a}, a \ne 0$
Opóźnienie
Załóżmy, że sygnał y (t) jest wynikiem splotu dwóch sygnałów x1 (t) i x2 (t). Jeżeli oba sygnały są opóźnione odpowiednio o czas t1 i t2, to wynikowy sygnał y (t) będzie opóźniony o (t1 + t2). Matematycznie można to zapisać jako -
Gdyby, $x_{1}(t)*x_{2}(t) = y(t)$
Następnie, $x_{1}(t-t_{1})*x_{2}(t-t_{2}) = y[t-(t_{1}+t_{2})]$
Rozwiązane przykłady
Example 1 - Znajdź splot sygnałów u (t-1) i u (t-2).
Solution- Dane sygnały to u (t-1) iu (t-2). Ich splot można wykonać, jak pokazano poniżej -
$y(t) = u(t-1)*u(t-2)$
$y(t) = \int_{-\infty}^{+\infty}[u(t-1).u(t-2)]dt$
$= r(t-1)+r(t-2)$
$= r(t-3)$
Example 2 - Znajdź splot dwóch sygnałów podanych przez
$x_{1}(n) = \lbrace 3,-2, 2\rbrace $
$x_{2}(n) = \begin{cases}2, & 0\leq n\leq 4\\0, & x > elsewhere\end{cases}$
Solution -
x 2 (n) można zdekodować jako$x_{2}(n) = \lbrace 2,2,2,2,2\rbrace Originalfirst$
x 1 (n) zostało podane wcześniej$= \lbrace 3,-2,3\rbrace = 3-2Z^{-1}+2Z^{-2}$
Podobnie, $x_{2}(z) = 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$
Sygnał wynikowy,
$X(Z) = X_{1}(Z)X_{2}(z)$
$= \lbrace 3-2Z^{-1}+2Z^{-2}\rbrace \times \lbrace 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}\rbrace$
$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+6Z^{-4}+6Z^{-5}$
Biorąc pod uwagę odwrotną transformację Z powyższego, otrzymamy wynikowy sygnał jako
$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$ Początek na początku
Example 3 - Wyznacz splot kolejnych 2 sygnałów -
$x(n) = \lbrace 2,1,0,1\rbrace$
$h(n) = \lbrace 1,2,3,1\rbrace$
Solution -
Biorąc transformację Z sygnałów, otrzymujemy:
$x(z) = 2+2Z^{-1}+2Z^{-3}$
I $h(n) = 1+2Z^{-1}+3Z^{-2}+Z^{-3}$
Teraz splot dwóch sygnałów oznacza zwielokrotnienie ich transformacji Z.
To jest $Y(Z) = X(Z) \times h(Z)$
$= \lbrace 2+2Z^{-1}+2Z^{-3}\rbrace \times \lbrace 1+2Z^{-1}+3Z^{-2}+Z^{-3}\rbrace$
$= \lbrace 2+5Z^{-1}+8Z^{-2}+6Z^{-3}+3Z^{-4}+3Z^{-5}+Z^{-6}\rbrace$
Biorąc pod uwagę odwrotną transformację Z, wynikowy sygnał można zapisać jako;
$y(n) = \lbrace 2,5,8,6,6,1 \rbrace Originalfirst$
Niektóre systemy mają informacje zwrotne, a inne nie. Te, które nie mają systemów sprzężenia zwrotnego, ich wyjście zależy tylko od aktualnych wartości wejścia. Dotychczasowa wartość danych nie jest obecnie obecna. Tego typu systemy są znane jako systemy statyczne. Nie zależy też od przyszłych wartości.
Ponieważ te systemy nie mają żadnych przeszłych zapisów, więc nie mają również żadnej pamięci. Dlatego mówimy, że wszystkie systemy statyczne są systemami bez pamięci. Weźmy przykład, aby lepiej zrozumieć tę koncepcję.
Przykład
Sprawdźmy, czy poniższe systemy są systemami statycznymi, czy nie.
- $y(t) = x(t)+x(t-1)$
- $y(t) = x(2t)$
- $y(t) = x = \sin [x(t)]$
za) $y(t) = x(t)+x(t-1)$
Tutaj x (t) jest wartością bieżącą. Nie ma związku z wartościami z przeszłości. Jest to więc system statyczny. Jednak w przypadku x (t-1), jeśli wstawimy t = 0, zmniejszy się do x (-1), co jest zależne od przeszłej wartości. Więc to nie jest statyczne. Dlatego tutaj y (t) nie jest systemem statycznym.
b) $y(t) = x(2t)$
Jeśli podstawimy t = 2, wynikiem będzie y (t) = x (4). Znowu zależy to od przyszłej wartości. Nie jest to więc również system statyczny.
do) $y(t) = x = \sin [x(t)]$
W tym wyrażeniu mamy do czynienia z funkcją sinus. Zakres funkcji sinus wynosi od -1 do +1. Tak więc, niezależnie od wartości, które podstawimy za x (t), uzyskamy od -1 do +1. Dlatego możemy powiedzieć, że nie jest zależny od żadnych przeszłych ani przyszłych wartości. Dlatego jest to system statyczny.
Z powyższych przykładów możemy wyciągnąć następujące wnioski -
- Każdy system, w którym występuje przesunięcie czasu, nie jest statyczny.
- Każdy system z przesunięciem amplitudy również nie jest statyczny.
- Przypadki integracji i różnicowania również nie są statyczne.
Jeśli system zależy od przeszłej i przyszłej wartości sygnału w dowolnym momencie, to jest znany jako system dynamiczny. W przeciwieństwie do systemów statycznych nie są to systemy bez pamięci. Przechowują przeszłe i przyszłe wartości. Dlatego wymagają trochę pamięci. Zrozummy lepiej tę teorię na kilku przykładach.
Przykłady
Dowiedz się, czy poniższe systemy są dynamiczne.
a) $y(t) = x(t+1)$
W tym przypadku, jeśli wstawimy t = 1 do równania, zostanie on zamieniony na x (2), który jest wartością zależną od przyszłości. Ponieważ tutaj podajemy wejście jako 1, ale pokazuje on wartość dla x (2). Ponieważ jest to sygnał zależny od przyszłości, wyraźnie jest to system dynamiczny.
b) $y(t) = Real[x(t)]$
$$= \frac{[x(t)+x(t)^*]}{2}$$W tym przypadku, niezależnie od wartości, którą umieścimy, pokaże sygnał wartości rzeczywistej czasu. Nie ma zależności od przyszłych ani przeszłych wartości. Dlatego nie jest to system dynamiczny, a raczej system statyczny.
c) $y(t) = Even[x(t)]$
$$= \frac{[x(t)+x(-t)]}{2}$$Tutaj, jeśli podstawimy t = 1, jeden sygnał pokaże x (1), a drugi pokaże x (-1), który jest wartością przeszłą. Podobnie, jeśli wstawimy t = -1, jeden sygnał pokaże x (-1), a inny pokaże x (1), który jest wartością przyszłą. Dlatego oczywiście jest to przypadek systemu Dynamic.
d) $y(t) = \cos [x(t)]$
W tym przypadku, ponieważ system jest funkcją cosinus, ma pewną dziedzinę wartości, która mieści się w zakresie od -1 do +1. Dlatego jakiekolwiek wartości, które umieścimy, otrzymamy wynik w określonym limicie. Dlatego jest to system statyczny
Z powyższych przykładów możemy wyciągnąć następujące wnioski -
- Wszystkie sygnały przypadków przesunięcia w czasie są sygnałami dynamicznymi.
- Również w przypadku skalowania czasu wszystkie sygnały są sygnałami dynamicznymi.
- Sygnały przypadków integracji są sygnałami dynamicznymi.
Wcześniej widzieliśmy, że system musi być niezależny od przyszłych i przeszłych wartości, aby stał się statyczny. W tym przypadku stan jest prawie taki sam z niewielkimi modyfikacjami. Tutaj, aby system był przyczynowy, powinien być niezależny tylko od przyszłych wartości. Oznacza to, że dawna zależność nie spowoduje, że system stanie się przyczyną.
Systemy przyczynowe są systemami możliwymi do zrealizowania praktycznie lub fizycznie. Rozważmy kilka przykładów, aby lepiej to zrozumieć.
Przykłady
Rozważmy następujące sygnały.
a) $y(t) = x(t)$
Tutaj sygnał jest zależny tylko od aktualnych wartości x. Na przykład, jeśli podstawimy t = 3, wynik będzie pokazywany tylko dla tej chwili. Dlatego, ponieważ nie ma zależności od przyszłej wartości, możemy nazwać go systemem przyczynowym.
b) $y(t) = x(t-1)$
Tutaj system zależy od przeszłych wartości. Na przykład, jeśli podstawimy t = 3, wyrażenie zmniejszy się do x (2), co jest wartością przeszłą w stosunku do naszego wejścia. W żadnym wypadku nie zależy to od przyszłych wartości. Dlatego ten system jest również systemem przyczynowym.
c) $y(t) = x(t)+x(t+1)$
W tym przypadku system składa się z dwóch części. Część x (t), jak omówiliśmy wcześniej, zależy tylko od aktualnych wartości. Więc nie ma z tym problemu. Jeśli jednak weźmiemy przypadek x (t + 1), to wyraźnie zależy to od przyszłych wartości, ponieważ jeśli wstawimy t = 1, wyrażenie zmniejszy się do x (2), co jest wartością przyszłą. Dlatego nie jest to przyczynowe.
System bez przyczynowy jest przeciwieństwem systemu przyczynowego. Jeśli system zależy od przyszłych wartości danych wejściowych w dowolnym momencie, to mówi się, że jest to system bez przyczynowy.
Przykłady
Weźmy kilka przykładów i spróbujmy to lepiej zrozumieć.
a) $y(t) = x(t+1)$
Omówiliśmy już ten system również w systemie przyczynowym. Dla każdego wejścia zredukuje system do jego przyszłej wartości. Na przykład, jeśli wstawimy t = 2, zmniejszy się do x (3), co jest wartością przyszłą. Dlatego system nie jest przyczynowy.
b) $y(t) = x(t)+x(t+2)$
W tym przypadku x (t) jest wyłącznie funkcją zależną od wartości bieżącej. Omówiliśmy już, że funkcja x (t + 2) jest zależna od przyszłości, ponieważ dla t = 3 da wartości dla x (5). Dlatego nie jest przyczyną.
c) $y(t) = x(t-1)+x(t)$
W tym systemie zależy to od obecnych i przeszłych wartości danego wejścia. Jakiekolwiek wartości zastąpimy, nigdy nie wykażą one żadnej przyszłej zależności. Oczywiście nie jest to system bezprzyczynowy; jest to raczej system przyczynowy.
System przeciwdziałający przyczynom to tylko trochę zmodyfikowana wersja systemu bez przyczynowego. System zależy tylko od przyszłych wartości wejścia. Nie ma zależności ani od obecnych, ani od przeszłych wartości.
Przykłady
Dowiedz się, czy poniższe systemy są anty-przyczynowe.
a) $y(t) = x(t)+x(t-1)$
System ma dwie podfunkcje. Jedna podfunkcja x (t + 1) zależy od przyszłej wartości wejścia, ale inna podfunkcja x (t) zależy tylko od teraźniejszości. Ponieważ system jest zależny od wartości bieżącej również od wartości przyszłej, system ten nie jest anty-przyczynowy.
b) $y(t) = x(t+3)$
Jeśli przeanalizujemy powyższy układ, zobaczymy, że system zależy tylko od przyszłych wartości systemu, tj. Jeśli wstawimy t = 0, zmniejszy się on do x (3), co jest wartością przyszłą. Ten system jest doskonałym przykładem systemu przeciwdziałania przyczynom.
System liniowy podlega prawom superpozycji. Prawo to jest warunkiem koniecznym i wystarczającym do udowodnienia liniowości układu. Poza tym system jest połączeniem dwóch rodzajów praw -
- Prawo addytywności
- Prawo jednorodności

Na powyższych rysunkach przedstawiono zarówno prawo jednorodności, jak i prawo addytywności. Istnieją jednak inne warunki, aby sprawdzić, czy system jest liniowy, czy nie.
The conditions are -
- Wyjście powinno wynosić zero dla zerowego wejścia.
- W systemie nie powinno być żadnych operatorów nieliniowych.
Przykłady operatorów nieliniowych -
(a) Operatory trygonometryczne - Sin, Cos, Tan, Cot, Sec, Cosec itp.
(b) Wykładniczy, logarytmiczny, moduł, kwadrat, sześcian itp.
(c) sa (i / p), Sinc (i / p), Sqn (i / p) itp.
Ani wejście x, ani wyjście y nie powinny mieć tych operatorów nieliniowych.
Przykłady
Sprawdźmy, czy poniższe układy są liniowe.
a) $y(t) = x(t)+3$
Ten system nie jest systemem liniowym, ponieważ narusza pierwszy warunek. Jeśli ustawimy wejście na zero, dzięki czemu x (t) = 0, to wynik nie będzie zerowy.
b) $y(t) = \sin tx(t)$
W tym systemie, jeśli damy wejście jako zero, wyjście będzie równe zero. Stąd pierwszy warunek jest wyraźnie spełniony. Ponownie, nie ma operatora nieliniowego, który zostałby zastosowany do x (t). Zatem drugi warunek jest również spełniony. Dlatego system jest systemem liniowym.
c) $y(t) = \sin (x(t))$
W powyższym systemie pierwszy warunek jest spełniony, ponieważ jeśli wstawimy x (t) = 0, na wyjściu również będzie sin (0) = 0. Jednak drugi warunek nie jest spełniony, ponieważ istnieje operator nieliniowy, który działa x (t). Dlatego system nie jest liniowy.
Jeśli chcemy zdefiniować ten system, możemy powiedzieć, że układy, które nie są liniowe, są systemami nieliniowymi. Oczywiście wszystkie warunki, które są naruszane w układach liniowych, powinny być w tym przypadku spełnione.
Warunki
Wyjście nie powinno być zerowe, gdy zastosowane wejście wynosi zero.
Na wejściu lub wyjściu można zastosować dowolny operator nieliniowy, aby uczynić system nieliniowym.
Przykłady
Aby dowiedzieć się, czy dane układy są liniowe czy nieliniowe.
a) $y(t) = e^{x(t)}$
W powyższym systemie pierwszy warunek jest spełniony, ponieważ jeśli wprowadzimy na wejściu zero, otrzymamy wynik 1. Dodatkowo do wejścia stosowany jest wykładniczy operator nieliniowy. Oczywiście jest to przypadek systemu nieliniowego.
b) $y(t) = x(t+1)+x(t-1)$
Powyższy typ systemu dotyczy zarówno przeszłych, jak i przyszłych wartości. Jeśli jednak wprowadzimy jego wartość jako zero, wówczas żadna z jego wartości nie istnieje. Dlatego możemy powiedzieć, że jeśli wejście ma wartość zero, to przeskalowana w czasie i przesunięta w czasie wersja wejścia również będzie równa zero, co narusza nasz pierwszy warunek. Ponownie, nie ma operatora nieliniowego. Dlatego naruszony jest również drugi warunek. Oczywiście ten system nie jest systemem nieliniowym; jest to raczej system liniowy.
W przypadku systemu niezmiennego w czasie wyjście i wejście powinny być opóźnione o jakąś jednostkę czasu. Każde opóźnienie podane na wejściu musi być odzwierciedlone na wyjściu w systemie niezmiennym w czasie.
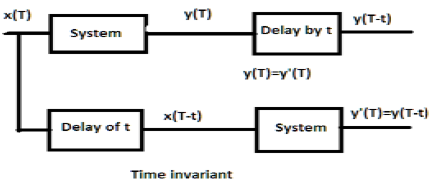
Przykłady
a) $y(T) = x(2T)$
Jeśli powyższe wyrażenie, najpierw przechodzi przez system, a następnie przez opóźnienie czasowe (jak pokazano w górnej części rysunku); wtedy dane wyjściowe staną się$x(2T-2t)$. Teraz to samo wyrażenie przechodzi najpierw przez opóźnienie czasowe, a następnie przez system (jak pokazano w dolnej części rysunku). Dane wyjściowe staną się$x(2T-t)$.
Dlatego system nie jest systemem niezmiennym w czasie.
b) $y(T) = \sin [x(T)]$
Jeśli sygnał jest najpierw przepuszczany przez system, a następnie przez proces opóźnienia czasowego, na wyjściu jest $\sin x(T-t)$. Podobnie, jeśli system najpierw przejdzie przez opóźnienie czasowe, a następnie przez system, wtedy wyjście będzie$\sin x(T-t)$. Widzimy wyraźnie, że oba wyjścia są takie same. Dlatego system jest niezmienny w czasie.
W przypadku systemu o wariancie czasowym również wyjście i wejście powinny być opóźnione o pewną stałą czasową, ale opóźnienie na wejściu nie powinno odzwierciedlać na wyjściu. Wszystkie przypadki skalowania czasu są przykładami systemu wariantowego. Podobnie, gdy współczynnik w relacji systemowej jest funkcją czasu, to również system jest zmienny w czasie.
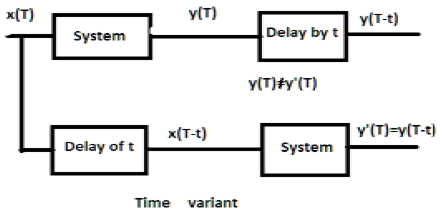
Przykłady
a) $y(t) = x[\cos T]$
Jeśli powyższy sygnał zostanie najpierw przepuszczony przez system, a następnie przez opóźnienie czasowe, wyjście będzie $x\cos (T-t)$. Jeśli najpierw przejdzie przez opóźnienie czasowe, a następnie przez system, będzie$x(\cos T-t)$. Ponieważ wyjścia nie są takie same, system jest zmienny czasowo.
b) $y(T) = \cos T.x(T)$
Jeśli powyższe wyrażenie zostanie najpierw przepuszczone przez system, a następnie przez opóźnienie czasowe, to wyjście będzie $\cos(T-t)x(T-t)$. Jeśli jednak wyrażenie zostanie najpierw przepuszczone przez opóźnienie czasowe, a następnie przez system, wynik będzie$\cos T.x(T-t)$. Ponieważ wyjścia nie są takie same, system jest oczywiście zmienny czasowo.
Stabilny system spełnia warunek BIBO (ograniczone wejście dla ograniczonego wyjścia). Tutaj ograniczony oznacza skończoną amplitudę. Dla stabilnego systemu, wyjście powinno być ograniczone lub skończone, dla skończonych lub ograniczonych danych wejściowych, w każdej chwili.
Niektóre przykłady ograniczonych wejść to funkcje sinus, cosinus, DC, signum i krok jednostkowy.
Przykłady
a) $y(t) = x(t)+10$
Tutaj, dla określonego ograniczonego wejścia, możemy otrzymać określone ograniczone wyjście, tj. Jeśli wstawimy $x(t) = 2, y(t) = 12$który ma charakter ograniczony. Dlatego system jest stabilny.
b) $y(t) = \sin [x(t)]$
W podanym wyrażeniu wiemy, że funkcje sinusowe mają określoną granicę wartości, która leży między -1 a +1. Zatem bez względu na wartości, które podstawimy przy x (t), otrzymamy wartości mieszczące się w naszych granicach. Dlatego system jest stabilny.
Niestabilne systemy nie spełniają warunków BIBO. Dlatego w przypadku ograniczonego wejścia nie możemy oczekiwać ograniczonego wyjścia w przypadku niestabilnych systemów.
Przykłady
a) $y(t) = tx(t)$
Tutaj, dla skończonych danych wejściowych, nie możemy oczekiwać skończonych danych wyjściowych. Na przykład, jeśli umieścimy$x(t) = 2 \Rightarrow y(t) = 2t$. Nie jest to wartość skończona, ponieważ nie znamy wartości t. Tak więc można go uzyskać z dowolnego miejsca. Dlatego ten system nie jest stabilny. To jest niestabilny system.
b) $y(t) = \frac{x(t)}{\sin t}$
Omówiliśmy wcześniej, że funkcja sinus ma określony zakres od -1 do +1; ale tutaj jest obecny w mianowniku. Tak więc w najgorszym przypadku, jeśli ustawimy t = 0, a funkcja sinus osiągnie zero, to cały system będzie dążył do nieskończoności. Dlatego ten typ systemu wcale nie jest stabilny. Oczywiście jest to niestabilny system.
Example 1 - Sprawdź, czy $y(t) = x*(t)$ jest liniowy lub nieliniowy.
Solution- Funkcja reprezentuje sprzężenie danych wejściowych. Można to zweryfikować albo za pomocą pierwszego prawa jednorodności i prawa addytywności, albo za pomocą dwóch reguł. Jednak weryfikacja za pomocą reguł jest znacznie łatwiejsza, więc będziemy się tym zajmować.
Jeśli wejście do systemu wynosi zero, wyjście również zmierza do zera. Dlatego nasz pierwszy warunek jest spełniony. Nie ma operatora nieliniowego używanego ani na wejściu, ani na wyjściu. Dlatego system jest liniowy.
Example 2 - Sprawdź, czy $y(t)=\begin{cases}x(t+1), & t > 0\\x(t-1), & t\leq 0\end{cases}$ jest liniowa lub nieliniowa
Solution- Oczywiście widzimy, że kiedy czas staje się mniejszy lub równy zero, wejście staje się zerowe. Możemy więc powiedzieć, że przy zerowym wejściu wyjście również wynosi zero i nasz pierwszy warunek jest spełniony.
Ponownie, nie ma operatora nieliniowego używanego na wejściu ani na wyjściu. Dlatego system jest liniowy.
Example 3 - Sprawdź, czy $y(t) = \sin t.x(t)$ jest stabilny, czy nie.
Solution - Załóżmy, że przyjęliśmy wartość x (t) jako 3. Tutaj funkcja sinus została przez nią pomnożona, a maksymalna i minimalna wartość funkcji sinus waha się od -1 do +1.
Dlatego maksymalna i minimalna wartość całej funkcji również będzie się wahać między -3 a +3. W ten sposób system jest stabilny, ponieważ tutaj otrzymujemy ograniczone dane wejściowe dla ograniczonego wyjścia.
Istnieje dyskretna transformata Fouriera w czasie (DTFT) dla sygnałów energii i mocy. Transformacja Z nie istnieje również dla sygnału typu energii ani mocy (NENP), tylko do pewnego stopnia. Zastąpienie$z=e^{jw}$ jest używany do konwersji Z-transformacji na DTFT tylko dla absolutnie sumowalnego sygnału.
Zatem transformację Z dyskretnego sygnału czasu x (n) w szeregu potęg można zapisać jako -
$$X(z) = \sum_{n-\infty}^\infty x(n)Z^{-n}$$Powyższe równanie przedstawia równanie dwustronnej transformacji Z.
Generalnie, gdy sygnał jest przekształcany w Z, można go przedstawić jako -
$$X(Z) = Z[x(n)]$$Lub $x(n) \longleftrightarrow X(Z)$
Jeśli jest to ciągły sygnał czasu, transformacje Z nie są potrzebne, ponieważ używane są transformacje Laplace'a. Jednak dyskretne sygnały czasowe mogą być analizowane tylko za pomocą transformacji Z.
Region konwergencji
Region zbieżności to zakres zmiennej zespolonej Z w płaszczyźnie Z. Transformacja Z sygnału jest skończona lub zbieżna. Tak więc ROC reprezentuje ten zbiór wartości Z, dla których X (Z) ma skończoną wartość.
Właściwości ROC
- ROC nie obejmuje tyczki.
- Dla sygnału prawostronnego ROC będzie poza okręgiem w płaszczyźnie Z.
- Dla sygnału lewostronnego, ROC będzie wewnątrz koła w płaszczyźnie Z.
- Aby zapewnić stabilność, ROC zawiera koło jednostkowe w płaszczyźnie Z.
- Dla sygnału dwustronnego ROC jest pierścieniem w płaszczyźnie Z.
- Dla sygnału o skończonym czasie trwania ROC to cała płaszczyzna Z.
Przekształcenie Z charakteryzuje się wyjątkowo:
- Wyrażenie X (Z)
- ROC z X (Z)
Sygnały i ich ROC
| x (n) | X (Z) | ROC |
|---|---|---|
| $\delta(n)$ | $1$ | Cała płaszczyzna Z. |
| $U(n)$ | $1/(1-Z^{-1})$ | Mod (Z)> 1 |
| $a^nu(n)$ | $1/(1-aZ^{-1})$ | Mod (Z)> Mod (a) |
| $-a^nu(-n-1)$ | $1/(1-aZ^{-1})$ | Mod (Z) <Mod (a) |
| $na^nu(n)$ | $aZ^{-1}/(1-aZ^{-1})^2$ | Mod (Z)> Mod (a) |
| $-a^nu(-n-1)$ | $aZ^{-1}/(1-aZ^{-1})^2$ | Mod (Z) <Mod (a) |
| $U(n)\cos \omega n$ | $(Z^2-Z\cos \omega)/(Z^2-2Z \cos \omega +1)$ | Mod (Z)> 1 |
| $U(n)\sin \omega n$ | $(Z\sin \omega)/(Z^2-2Z \cos \omega +1)$ | Mod (Z)> 1 |
Przykład
Znajdźmy transformację Z i ROC sygnału podanego jako $x(n) = \lbrace 7,3,4,9,5\rbrace$, gdzie początek serii to 3.
Solution - Stosowanie wzoru, który mamy -
$X(z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$
$= \sum_{n=-1}^3 x(n)Z^{-n}$
$= x(-1)Z+x(0)+x(1)Z^{-1}+x(2)Z^{-2}+x(3)Z^{-3}$
$= 7Z+3+4Z^{-1}+9Z^{-2}+5Z^{-3}$
ROC to cała płaszczyzna Z z wyłączeniem Z = 0, ∞, -∞
W tym rozdziale zrozumiemy podstawowe właściwości przekształceń Z.
Liniowość
Stwierdza, że gdy dwa lub więcej indywidualnych sygnałów dyskretnych jest pomnożonych przez stałe, ich odpowiednie transformaty Z również zostaną pomnożone przez te same stałe.
Matematycznie,
$$a_1x_1(n)+a_2x_2(n) = a_1X_1(z)+a_2X_2(z)$$Proof - wiemy, że
$$X(Z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$$$= \sum_{n=-\infty}^\infty (a_1x_1(n)+a_2x_2(n))Z^{-n}$
$= a_1\sum_{n = -\infty}^\infty x_1(n)Z^{-n}+a_2\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$
$= a_1X_1(z)+a_2X_2(z)$ (Stąd udowodniono)
Tutaj jest ROC $ROC_1\bigcap ROC_2$.
Przesunięcie w czasie
Właściwość przesunięcia w czasie przedstawia, jak zmiana w dziedzinie czasu w sygnale dyskretnym wpłynie na domenę Z, którą można zapisać jako;
$$x(n-n_0)\longleftrightarrow X(Z)Z^{-n}$$Lub $x(n-1)\longleftrightarrow Z^{-1}X(Z)$
Proof -
Pozwolić $y(P) = X(P-K)$
$Y(z) = \sum_{p = -\infty}^\infty y(p)Z^{-p}$
$= \sum_{p = -\infty}^\infty (x(p-k))Z^{-p}$
Niech s = pk
$= \sum_{s = -\infty}^\infty x(s)Z^{-(s+k)}$
$= \sum_{s = -\infty}^\infty x(s)Z^{-s}Z^{-k}$
$= Z^{-k}[\sum_{s=-\infty}^\infty x(m)Z^{-s}]$
$= Z^{-k}X(Z)$ (Stąd udowodniono)
Tutaj ROC można zapisać jako Z = 0 (p> 0) lub Z = ∞ (p <0)
Przykład
U (n) i U (n-1) można wykreślić w następujący sposób
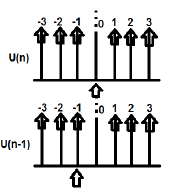
Transformację Z U (n) cab należy zapisać jako;
$\sum_{n = -\infty}^\infty [U(n)]Z^{-n} = 1$
Transformację Z U (n-1) można zapisać jako;
$\sum_{n = -\infty}^\infty [U(n-1)]Z^{-n} = Z^{-1}$
Więc tu $x(n-n_0) = Z^{-n_0}X(Z)$ (Stąd udowodniono)
Skalowanie czasu
Właściwość skalowania czasu mówi nam, jaka będzie dziedzina Z sygnału, gdy czas jest skalowany w postaci dyskretnej, którą można zapisać jako;
$$a^nx(n) \longleftrightarrow X(a^{-1}Z)$$Proof -
Pozwolić $y(p) = a^{p}x(p)$
$Y(P) = \sum_{p=-\infty}^\infty y(p)Z^{-p}$
$= \sum_{p=-\infty}^\infty a^px(p)Z^{-p}$
$= \sum_{p=-\infty}^\infty x(p)[a^{-1}Z]^{-p}$
$= X(a^{-1}Z)$(Stąd udowodniono)
ROC: = Mod (ar1) <Mod (Z) <Mod (ar2) gdzie Mod = Modulus
Przykład
Określmy transformację Z. $x(n) = a^n \cos \omega n$ przy użyciu właściwości skalowania czasu.
Solution -
Wiemy już, że transformacja Z sygnału $\cos (\omega n)$ jest dane przez -
$$\sum_{n=-\infty}^\infty(\cos \omega n)Z^{-n} = (Z^2-Z \cos \omega)/(Z^2-2Z\cos \omega +1)$$
Teraz, stosując właściwość Skalowanie czasu, transformacja Z $a^n \cos \omega n$ można zapisać jako;
$\sum_{n=-\infty}^\infty(a^n\cos \omega n)Z^{-n} = X(a^{-1}Z)$
$= [(a^{-1}Z)^2-(a^{-1}Z \cos \omega n)]/((a^{-1}Z)^2-2(a^{-1}Z \cos \omega n)+1)$
$= Z(Z-a \cos \omega)/(Z^2-2az \cos \omega+a^2)$
Sukcesywne różnicowanie
Właściwość Successive Differentiation pokazuje, że transformacja Z nastąpi, gdy zróżnicujemy dyskretny sygnał w dziedzinie czasu w odniesieniu do czasu. Jest to pokazane poniżej.
$$\frac{dx(n)}{dn} = (1-Z^{-1})X(Z)$$Proof -
Rozważ LHS równania - $\frac{dx(n)}{dn}$
$$= \frac{[x(n)-x(n-1)]}{[n-(n-1)]}$$$= x(n)-X(n-1)$
$= x(Z)-Z^{-1}x(Z)$
$= (1-Z^{-1})x(Z)$ (Stąd udowodniono)
ROC: R1 <Mod (Z) <R2
Przykład
Znajdźmy transformację Z sygnału podanego przez $x(n) = n^2u(n)$
Według własności możemy pisać
$Zz[nU(n)] = -Z\frac{dZ[U(n)]}{dz}$
$= -Z\frac{d[\frac{Z}{Z-1}]}{dZ}$
$= Z/((Z-1)^2$
$= y(let)$
Teraz Z [ny] można się dowiedzieć, ponownie stosując właściwość,
$Z(n,y) = -Z\frac{dy}{dz}$
$= -Z\frac{d[Z/(Z-1)^3]}{dz}$
$= Z(Z+1)/(Z-1)^2$
Skręt
Przedstawia zmianę w domenie Z systemu, gdy splot ma miejsce w postaci sygnału dyskretnego, który można zapisać jako -
$x_1(n)*x_2(n) \longleftrightarrow X_1(Z).X_2(Z)$
Proof -
$X(Z) = \sum_{n = -\infty}^\infty x(n)Z^{-n}$
$= \sum_{n=-\infty}^\infty[\sum_{k = -\infty}^\infty x_1(k)x_2(n-k)]Z^{-n}$
$= \sum_{k = -\infty}^\infty x_1(k)[\sum_n^\infty x_2(n-k)Z^{-n}]$
$= \sum_{k = -\infty}^\infty x_1(k)[\sum_{n = -\infty}^\infty x_2(n-k)Z^{-(n-k)}Z^{-k}]$
Niech nk = l, to powyższe równanie cab zapisujemy jako -
$X(Z) = \sum_{k = -\infty}^\infty x_1(k)[Z^{-k}\sum_{l=-\infty}^\infty x_2(l)Z^{-l}]$
$= \sum_{k = -\infty}^\infty x_1(k)X_2(Z)Z^{-k}$
$= X_2(Z)\sum_{k = -\infty}^\infty x_1(Z)Z^{-k}$
$= X_1(Z).X_2(Z)$ (Stąd udowodniono)
ROC:$ROC\bigcap ROC2$
Przykład
Znajdźmy splot danych dwóch sygnałów
$x_1(n) = \lbrace 3,-2,2\rbrace$ ... (równ. 1)
$x_2(n) = \lbrace 2,0\leq 4\quad and\quad 0\quad elsewhere\rbrace$ ... (równ. 2)
Transformację Z pierwszego równania można zapisać jako;
$\sum_{n = -\infty}^\infty x_1(n)Z^{-n}$
$= 3-2Z^{-1}+2Z^{-2}$
Transformację Z drugiego sygnału można zapisać jako;
$\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$
$= 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$
Tak więc splot powyższych dwóch sygnałów jest określony przez -
$X(Z) = [x_1(Z)^*x_2(Z)]$
$= [3-2Z^{-1}+2Z^{-2}]\times [2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}]$
$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+...\quad...\quad...$
Biorąc odwrotną transformację Z otrzymujemy,
$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$
Twierdzenie o wartości początkowej
Jeśli x (n) jest ciągiem przyczynowym, którego transformacja Z wynosi X (z), to twierdzenie o wartości początkowej można zapisać jako;
$X(n)(at\quad n = 0) = \lim_{z \to \infty} X(z)$
Proof - wiemy, że
$X(Z) = \sum_{n = 0} ^\infty x(n)Z^{-n}$
Rozszerzając powyższą serię, otrzymujemy;
$= X(0)Z^0+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$
$= X(0)\times 1+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$
W powyższym przypadku, jeśli Z → ∞ to $Z^{-n}\rightarrow 0$ (Ponieważ n> 0)
Dlatego możemy powiedzieć;
$\lim_{z \to \infty}X(z) = X(0)$ (Stąd udowodniono)
Twierdzenie o wartości końcowej
Twierdzenie o wartości końcowej stwierdza, że jeśli transformacja Z sygnału jest reprezentowana jako X (Z), a wszystkie bieguny znajdują się wewnątrz koła, to jego ostateczna wartość jest oznaczona jako x (n) lub X (∞) i może być zapisana jako -
$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$
Conditions -
- Ma zastosowanie tylko do systemów przyczynowych.
- $X(Z)(1-Z^{-1})$ powinny mieć bieguny wewnątrz okręgu jednostkowego w płaszczyźnie Z.
Proof - Wiemy o tym
$Z^+[x(n+1)-x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$
$\Rightarrow Z^+[x(n+1)]-Z^+[x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$
$\Rightarrow Z[X(Z)^+-x(0)]-X(Z)^+ = \lim_{k \to \infty}\sum_{n = 0}^kZ^{-n}[x(n+1)-x(n)]$
Tutaj możemy zastosować zaawansowaną właściwość jednostronnej transformacji Z. Zatem powyższe równanie można ponownie zapisać jako;
$Z^+[x(n+1)] = Z[X(2)^+-x(0)Z^0] = Z[X(Z)^+-x(0)]$
Teraz umieszczając z = 1 w powyższym równaniu, możemy rozszerzyć powyższe równanie -
$\lim_{k \to \infty}{[x(1)-x(0)+x(6)-x(1)+x(3)-x(2)+...\quad...\quad...+x(x+1)-x(k)]}$
Można to sformułować jako;
$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$(Stąd udowodniono)
Przykład
Znajdźmy początkową i końcową wartość x (n), której sygnał jest dany przez
$X(Z) = 2+3Z^{-1}+4Z^{-2}$
Solution - Najpierw znajdźmy wartość początkową sygnału, stosując twierdzenie
$x(0) = \lim_{z \to \infty}X(Z)$
$= \lim_{z \to \infty}[2+3Z^{-1}+4Z^{-2}]$
$= 2+(\frac{3}{\infty})+(\frac{4}{\infty}) = 2$
Teraz znajdźmy ostateczną wartość sygnału stosując twierdzenie
$x(\infty) = \lim_{z \to \infty}[(1-Z^{-1})X(Z)]$
$= \lim_{z \to \infty}[(1-Z^{-1})(2+3Z^{-1}+4Z^{-2})]$
$= \lim_{z \to \infty}[2+Z^{-1}+Z^{-2}-4Z^{-3}]$
$= 2+1+1-4 = 0$
Some other properties of Z-transform are listed below -
Zróżnicowanie częstotliwości
Daje zmianę w domenie Z sygnału, gdy jego dyskretny sygnał jest zróżnicowany w czasie.
$nx(n)\longleftrightarrow -Z\frac{dX(z)}{dz}$
Jego ROC można zapisać jako;
$r_2< Mod(Z)< r_1$
Przykład
Znajdźmy wartość x (n) poprzez Zróżnicowanie częstotliwości, której dyskretny sygnał w dziedzinie Z jest określony przez $x(n)\longleftrightarrow X(Z) = log(1+aZ^{-1})$
Według własności możemy to napisać
$nx(n)\longleftrightarrow -Z\frac{dx(Z)}{dz}$
$= -Z[\frac{-aZ^{-2}}{1+aZ^{-1}}]$
$= (aZ^{-1})/(1+aZ^{-1})$
$= 1-1/(1+aZ^{-1})$
$nx(n) = \delta(n)-(-a)^nu(n)$
$\Rightarrow x(n) = 1/n[\delta(n)-(-a)^nu(n)]$
Mnożenie w czasie
Daje zmianę w domenie Z sygnału, gdy mnożenie odbywa się na poziomie sygnału dyskretnego.
$x_1(n).x_2(n)\longleftrightarrow(\frac{1}{2\Pi j})[X1(Z)*X2(Z)]$
Koniugacja w czasie
To przedstawia reprezentację sprzężonego dyskretnego sygnału w domenie Z.
$X^*(n)\longleftrightarrow X^*(Z^*)$
System, który pełni funkcję systemową, może być stabilny tylko wtedy, gdy wszystkie bieguny leżą wewnątrz okręgu jednostkowego. Najpierw sprawdzamy, czy system jest przyczynowy, czy nie. Jeśli system jest przyczynowy, to idziemy do jego określenia stabilności BIBO; gdzie stabilność BIBO odnosi się do ograniczonego wejścia dla ograniczonego warunku wyjściowego.
Można to zapisać jako;
$Mod(X(Z))< \infty$
$= Mod(\sum x(n)Z^{-n})< \infty$
$= \sum Mod(x(n)Z^{-n})< \infty$
$= \sum Mod[x(n)(re^{jw})^{-n}]< 0$
$= \sum Mod[x(n)r^{-n}]Mod[e^{-jwn}]< \infty$
$= \sum_{n = -\infty}^\infty Mod[x(n)r^{-n}]< \infty$
Powyższe równanie pokazuje warunek istnienia transformacji Z.
Jednak warunkiem istnienia sygnału DTFT jest
$$\sum_{n = -\infty}^\infty Mod(x(n)< \infty$$Przykład 1
Spróbujmy znaleźć transformację Z sygnału, która jest podana jako
$x(n) = -(-0.5)^{-n}u(-n)+3^nu(n)$
$= -(-2)^nu(n)+3^nu(n)$
Solution - Tutaj, na $-(-2)^nu(n)$ ROC jest lewostronny, a Z <2
Dla $3^nu(n)$ ROC jest prawostronne, a Z> 3
Stąd tutaj transformacja Z sygnału nie będzie istnieć, ponieważ nie ma wspólnego regionu.
Przykład 2
Spróbujmy znaleźć transformację Z sygnału podanego przez
$x(n) = -2^nu(-n-1)+(0.5)^nu(n)$
Solution - Tutaj, na $-2^nu(-n-1)$ ROC sygnału jest lewostronny i Z <2
Na sygnał $(0.5)^nu(n)$ ROC jest prawostronne, a Z> 0,5
Tak więc wspólny ROC jest tworzony jako 0,5 <Z <2
Dlatego transformację Z można zapisać jako;
$X(Z) = \lbrace\frac{1}{1-2Z^{-1}}\rbrace+\lbrace\frac{1}{(1-0.5Z)^{-1}}\rbrace$
Przykład 3
Spróbujmy znaleźć transformację Z sygnału, która jest podana jako $x(n) = 2^{r(n)}$
Solution- r (n) jest sygnałem rampy. Zatem sygnał można zapisać jako;
$x(n) = 2^{nu(n)}\lbrace 1, n<0 (u(n)=0)\quad and\quad2^n, n\geq 0(u(n) = 1)\rbrace$
$= u(-n-1)+2^nu(n)$
Tutaj, dla sygnału $u(-n-1)$ i ROC Z <1 i dla $2^nu(n)$ z ROC wynosi Z> 2.
Tak więc transformacja Z sygnału nie będzie istnieć.
Z - Transformacja dla systemu przyczynowego
System przyczynowy można zdefiniować jako $h(n) = 0,n<0$. W przypadku systemu przyczynowego ROC będzie poza okręgiem w płaszczyźnie Z.
$H(Z) = \displaystyle\sum\limits_{n = 0}^{\infty}h(n)Z^{-n}$
Rozwinięcie powyższego równania,
$H(Z) = h(0)+h(1)Z^{-1}+h(2)Z^{-2}+...\quad...\quad...$
$= N(Z)/D(Z)$
W przypadku układów przyczynowych rozwinięcie Funkcji Transferu nie obejmuje dodatnich potęg Z. W przypadku układu przyczynowego rząd licznika nie może przekraczać rzędu mianownika. Można to zapisać jako-
$\lim_{z \rightarrow \infty}H(Z) = h(0) = 0\quad or\quad Finite$
Dla stabilności układu przyczynowego bieguny funkcji Transfer powinny znajdować się wewnątrz koła jednostkowego w płaszczyźnie Z.
Przekształcenie Z dla systemu przeciwdziałającego przyczynom
System anty-przyczynowy można zdefiniować jako $h(n) = 0, n\geq 0$. W przypadku systemu antyprzyczynowego bieguny funkcji transferu powinny leżeć poza okręgiem jednostkowym w płaszczyźnie Z. W przypadku systemu anty-przyczynowego ROC będzie wewnątrz koła w płaszczyźnie Z.
Jeśli chcemy przeanalizować system, który jest już reprezentowany w dziedzinie częstotliwości, jako dyskretny sygnał czasu, to przechodzimy do odwrotnej transformacji Z.
Matematycznie można to przedstawić jako;
$$x(n) = Z^{-1}X(Z)$$gdzie x (n) jest sygnałem w dziedzinie czasu, a X (Z) jest sygnałem w dziedzinie częstotliwości.
Jeśli chcemy przedstawić powyższe równanie w formacie całkowitym, możemy zapisać je jako
$$x(n) = (\frac{1}{2\Pi j})\oint X(Z)Z^{-1}dz$$Tutaj całka znajduje się po zamkniętej ścieżce C. Ta ścieżka znajduje się wewnątrz ROC x (z) i zawiera początek.
Metody znajdowania odwrotnej transformacji Z
Gdy potrzebna jest analiza w formacie dyskretnym, konwertujemy sygnał w dziedzinie częstotliwości z powrotem na format dyskretny poprzez odwrotną transformację Z. Postępujemy zgodnie z następującymi czterema sposobami określenia odwrotnej transformacji Z.
- Metoda długiego podziału
- Metoda częściowego rozszerzania frakcji
- Metoda całkowa resztkowa lub konturowa
Metoda długiego podziału
W tej metodzie transformację Z sygnału x (z) można przedstawić jako stosunek wielomianu, jak pokazano poniżej;
$$x(z)=N(Z)/D(Z)$$Jeśli teraz podzielimy licznik przez mianownik, otrzymamy szereg, jak pokazano poniżej
$$X(z) = x(0)+x(1)Z^{-1}+x(2)Z^{-2}+...\quad...\quad...$$Powyższa sekwencja reprezentuje serię odwrotnej transformacji Z danego sygnału (dla n≥0), a powyższy układ jest przyczynowy.
Jednak dla n <0 szereg można zapisać jako;
$$x(z) = x(-1)Z^1+x(-2)Z^2+x(-3)Z^3+...\quad...\quad...$$Metoda częściowego powiększania frakcji
Tutaj również sygnał jest najpierw wyrażany w postaci N (z) / D (z).
Jeśli jest to ułamek racjonalny, zostanie przedstawiony w następujący sposób;
$x(z) = b_0+b_1Z^{-1}+b_2Z^{-2}+...\quad...\quad...+b_mZ^{-m})/(a_0+a_1Z^{-1}+a_2Z^{-2}+...\quad...\quad...+a_nZ^{-N})$
Powyższy jest nieprawidłowy, gdy m <n i an ≠ 0
Jeśli stosunek nie jest właściwy (tj. Niewłaściwy), to musimy go przekonwertować do właściwej postaci, aby go rozwiązać.
Metoda całkowania pozostałości lub konturu
W tej metodzie otrzymujemy odwrotną transformację Z x (n) przez zsumowanie reszt $[x(z)Z^{n-1}]$na wszystkich biegunach. Matematycznie można to wyrazić jako
$$x(n) = \displaystyle\sum\limits_{all\quad poles\quad X(z)}residues\quad of[x(z)Z^{n-1}]$$Tutaj reszta dla dowolnego bieguna rzędu m przy $z = \beta$ jest
$$Residues = \frac{1}{(m-1)!}\lim_{Z \rightarrow \beta}\lbrace \frac{d^{m-1}}{dZ^{m-1}}\lbrace (z-\beta)^mX(z)Z^{n-1}\rbrace$$Przykład 1
Znajdź odpowiedź systemu $s(n+2)-3s(n+1)+2s(n) = \delta (n)$, gdy wszystkie warunki początkowe są zerowe.
Solution - Biorąc transformację Z po obu stronach powyższego równania, otrzymujemy
$$S(z)Z^2-3S(z)Z^1+2S(z) = 1$$$\Rightarrow S(z)\lbrace Z^2-3Z+2\rbrace = 1$
$\Rightarrow S(z) = \frac{1}{\lbrace z^2-3z+2\rbrace}=\frac{1}{(z-2)(z-1)} = \frac{\alpha _1}{z-2}+\frac{\alpha _2}{z-1}$
$\Rightarrow S(z) = \frac{1}{z-2}-\frac{1}{z-1}$
Biorąc odwrotną transformatę Z powyższego równania, otrzymujemy
$S(n) = Z^{-1}[\frac{1}{Z-2}]-Z^{-1}[\frac{1}{Z-1}]$
$= 2^{n-1}-1^{n-1} = -1+2^{n-1}$
Przykład 2
Znajdź funkcję systemu H (z) i odpowiedź próbki jednostkowej h (n) układu, którego równanie różnicowe opisano jako poniżej
$y(n) = \frac{1}{2}y(n-1)+2x(n)$
gdzie y (n) i x (n) są odpowiednio wyjściem i wejściem systemu.
Solution - Biorąc transformację Z powyższego równania różnicowego, otrzymujemy
$y(z) = \frac{1}{2}Z^{-1}Y(Z)+2X(z)$
$= Y(Z)[1-\frac{1}{2}Z^{-1}] = 2X(Z)$
$= H(Z) = \frac{Y(Z)}{X(Z)} = \frac{2}{[1-\frac{1}{2}Z^{-1}]}$
Ten system ma biegun w $Z = \frac{1}{2}$ i $Z = 0$ i $H(Z) = \frac{2}{[1-\frac{1}{2}Z^{-1}]}$
Stąd biorąc odwrotną transformatę Z powyższego, otrzymujemy
$h(n) = 2(\frac{1}{2})^nU(n)$
Przykład 3
Określ Y (z), n≥0 w następującym przypadku -
$y(n)+\frac{1}{2}y(n-1)-\frac{1}{4}y(n-2) = 0\quad given\quad y(-1) = y(-2) = 1$
Solution - Stosując transformację Z do powyższego równania, otrzymujemy
$Y(Z)+\frac{1}{2}[Z^{-1}Y(Z)+Y(-1)]-\frac{1}{4}[Z^{-2}Y(Z)+Z^{-1}Y(-1)+4(-2)] = 0$
$\Rightarrow Y(Z)+\frac{1}{2Z}Y(Z)+\frac{1}{2}-\frac{1}{4Z^2}Y(Z)-\frac{1}{4Z}-\frac{1}{4} = 0$
$\Rightarrow Y(Z)[1+\frac{1}{2Z}-\frac{1}{4Z^2}] =\frac{1}{4Z}-\frac{1}{2}$
$\Rightarrow Y(Z)[\frac{4Z^2+2Z-1}{4Z^2}] = \frac{1-2Z}{4Z}$
$\Rightarrow Y(Z) = \frac{Z(1-2Z)}{4Z^2+2Z-1}$
Podobnie jak ciągła transformata Fouriera sygnału czasu, dyskretna transformata Fouriera w czasie może być używana do reprezentowania dyskretnej sekwencji w jej równoważnej reprezentacji w dziedzinie częstotliwości i dyskretnego systemu czasu LTI oraz do opracowywania różnych algorytmów obliczeniowych.
X (jω) w ciągłym FT jest ciągłą funkcją x (n). Jednak DFT zajmuje się reprezentowaniem x (n) próbkami swojego widma X (ω). Dlatego to narzędzie matematyczne ma duże znaczenie obliczeniowe w wygodnej reprezentacji. Za pomocą tego narzędzia można przetwarzać zarówno sekwencje okresowe, jak i nieokresowe. Okresowe sekwencje muszą być próbkowane przez wydłużenie okresu do nieskończoności.
Próbkowanie w dziedzinie częstotliwości
Od wprowadzenia jest jasne, że musimy wiedzieć, jak przejść przez próbkowanie w dziedzinie częstotliwości, tj. Próbkowanie X (ω). W związku z tym związek między próbkowaną transformatą Fouriera a DFT jest ustalany w następujący sposób.
Podobnie, okresowe sekwencje można dopasować do tego narzędzia, wydłużając okres N do nieskończoności.
Niech będzie sekwencja nieokresowa, $X(n) = \lim_{N \to \infty}x_N(n)$
Definiowanie jego transformaty Fouriera,
$X(\omega ) = \sum_{n=-\infty}^\infty x(n)e^{-jwn}X(K\delta \omega)$
Tutaj X (ω) jest próbkowany okresowo, w każdym przedziale radianowym δω.
Ponieważ X (ω) jest okresowy w 2π radianach, potrzebujemy próbek tylko w zakresie podstawowym. Próbki pobiera się w jednakowo odległych odstępach w zakresie częstotliwości 0≤ω≤2π. Odstępy między równoważnymi przedziałami wynoszą$\delta \omega = \frac{2\pi }{N}k$ radian.
Teraz oceniając, $\omega = \frac{2\pi}{N}k$
$X(\frac{2\pi}{N}k) = \sum_{n = -\infty}^\infty x(n)e^{-j2\pi nk/N},$ ... eq (2)
gdzie k = 0,1, …… N-1
Po podzieleniu powyższych i zamianie kolejności sumowania
$X(\frac{2\pi}{N}k) = \displaystyle\sum\limits_{n = 0}^{N-1}[\displaystyle\sum\limits_{l = -\infty}^\infty x(n-Nl)]e^{-j2\pi nk/N}$ ... eq (3)
$\sum_{l=-\infty}^\infty x(n-Nl) = x_p(n) = a\quad periodic\quad function\quad of\quad period\quad N\quad and\quad its\quad fourier\quad series\quad = \sum_{k = 0}^{N-1}C_ke^{j2\pi nk/N}$
gdzie, n = 0,1,… .., N-1; „p” - oznacza okresową jednostkę lub funkcję
Współczynniki Fouriera to:
$C_k = \frac{1}{N}\sum_{n = 0}^{N-1}x_p(n)e^{-j2\pi nk/N}$k = 0,1,…, N-1 ... eq (4)
Porównując równania 3 i 4, otrzymujemy;
$NC_k = X(\frac{2\pi}{N}k)$k = 0,1,…, N-1 ... eq (5)
$NC_k = X(\frac{2\pi}{N}k) = X(e^{jw}) = \displaystyle\sum\limits_{n = -\infty}^\infty x_p(n)e^{-j2\pi nk/N}$... eq (6)
Z rozszerzenia serii Fouriera,
$x_p(n) = \frac{1}{N}\displaystyle\sum\limits_{k = 0}^{N-1}NC_ke^{j2\pi nk/N} = \frac{1}{N}\sum_{k = 0}^{N-1}X(\frac{2\pi}{N}k)e^{j2\pi nk/N}$... eq (7)
Gdzie n = 0,1,…, N-1
Tutaj otrzymaliśmy okresowy sygnał z X (ω). $x(n)$ można pobrać z $x_p(n)$ tylko wtedy, gdy nie ma aliasingu w dziedzinie czasu. $N\geq L$
N = okres $x_p(n)$ L = okres $x(n)$
$x(n) = \begin{cases}x_p(n), & 0\leq n\leq N-1\\0, & Otherwise\end{cases}$
W ten sposób uzyskuje się mapowanie.
Właściwości DFT
Liniowość
Stwierdza, że DFT kombinacji sygnałów jest równy sumie DFT poszczególnych sygnałów. Weźmy dwa sygnały x 1 (n) i x 2 (n), których DFT s to odpowiednio X 1 (ω) i X 2 (ω). Więc jeśli
$x_1(n)\rightarrow X_1(\omega)$i$x_2(n)\rightarrow X_2(\omega)$
Następnie $ax_1(n)+bx_2(n)\rightarrow aX_1(\omega)+bX_2(\omega)$
gdzie a i b są stałymi.
Symetria
Właściwości symetrii DFT można wyprowadzić w podobny sposób, jak wyprowadziliśmy właściwości symetrii DTFT. Wiemy, że DFT ciągu x (n) jest oznaczony przez X (K). Teraz, jeśli x (n) i X (K) są sekwencjami o wartościach zespolonych, to można je przedstawić jako pod
$x(n) = x_R(n)+jx_1(n),0\leq n\leq N-1$
I $X(K) = X_R(K)+jX_1(K),0\leq K\leq N-1$
Własność dualności
Rozważmy sygnał x (n), którego DFT jest podana jako X (K). Niech skończony czas trwania będzie X (N). Następnie zgodnie z twierdzeniem o dualności
Gdyby, $x(n)\longleftrightarrow X(K)$
Następnie, $X(N)\longleftrightarrow Nx[((-k))_N]$
Tak więc, używając tego twierdzenia, jeśli znamy DFT, możemy łatwo znaleźć sekwencję o skończonym czasie trwania.
Złożone właściwości sprzężone
Załóżmy, że istnieje sygnał x (n), którego DFT jest nam również znane jako X (K). Teraz, jeśli sprzężenie zespolone sygnału jest podane jako x * (n), wówczas możemy łatwo znaleźć DFT bez wykonywania wielu obliczeń, korzystając z poniższego twierdzenia.
Gdyby, $x(n)\longleftrightarrow X(K)$
Następnie, $x*(n)\longleftrightarrow X*((K))_N = X*(N-K)$
Kołowe przesunięcie częstotliwości
Mnożenie ciągu x (n) ze złożoną sekwencją wykładniczą $e^{j2\Pi kn/N}$jest równoważne kołowemu przesunięciu DFT o L jednostek częstotliwości. Jest to podwójna właściwość przesunięcia w czasie w trybie kołowym.
Gdyby, $x(n)\longleftrightarrow X(K)$
Następnie, $x(n)e^{j2\Pi Kn/N}\longleftrightarrow X((K-L))_N$
Mnożenie dwóch sekwencji
Jeśli istnieją dwa sygnały x 1 (n) i x 2 (n), a ich odpowiednie wartości DFT wynoszą X 1 (k) i X 2 (K), wówczas mnożenie sygnałów w sekwencji czasowej odpowiada kołowemu splotowi ich DFT.
Gdyby, $x_1(n)\longleftrightarrow X_1(K)\quad\&\quad x_2(n)\longleftrightarrow X_2(K)$
Następnie, $x_1(n)\times x_2(n)\longleftrightarrow X_1(K)© X_2(K)$
Twierdzenie Parsevala
Ogólnie dla sekwencji o wartościach zespolonych x (n) i y (n)
Gdyby, $x(n)\longleftrightarrow X(K)\quad \&\quad y(n)\longleftrightarrow Y(K)$
Następnie, $\sum_{n = 0}^{N-1}x(n)y^*(n) = \frac{1}{N}\sum_{k = 0}^{N-1}X(K)Y^*(K)$
Wiemy, kiedy $\omega = 2\pi K/N$ i $N\rightarrow \infty,\omega$ staje się zmienną ciągłą, a sumowanie granic staje się $-\infty$ do $+\infty$.
W związku z tym,
$$NC_k = X(\frac{2\pi}{N}k) = X(e^{j\omega}) = \displaystyle\sum\limits_{n = -\infty}^\infty x(n)e^{\frac{-j2\pi nk}{N}} = \displaystyle\sum\limits_{n = -\infty}^\infty x(n)e^{-j\omega n}$$Dyskretna transformata Fouriera w czasie (DTFT)
Wiemy to, $X(e^{j\omega}) = \sum_{n = -\infty}^\infty x(n)e^{-j\omega n}$
Gdzie, $X(e^{j\omega})$jest ciągła i okresowa w ω iz okresem 2π. … Eq (1)
Teraz,
$x_p(n) = \sum_{k = 0}^{N-1}NC_ke^{j2 \pi nk/N}$ … Z szeregu Fouriera
$x_p(n) = \frac{1}{2\pi}\sum_{k=0}^{N-1}NC_ke^{j2\pi nk/N}\times \frac{2\pi}{N}$
ω staje się ciągłe i $\frac{2\pi}{N}\rightarrow d\omega$z powodów przytoczonych powyżej.
$x(n) = \frac{1}{2\pi}\int_{n = 0}^{2\pi}X(e^{j\omega})e^{j\omega n}d\omega$… Eq (2)
Odwrotna transformacja Fouriera w czasie dyskretnym
Symbolicznie,
$x(n)\Longleftrightarrow x(e^{j\omega})$(Para transformacji Fouriera)
Warunek konieczny i wystarczający dla istnienia dyskretnej transformaty Fouriera w czasie dla nieokresowego ciągu x (n) jest bezwzględnie sumowalny.
to znaczy$\sum_{n = -\infty}^\infty|x(n)|<\infty$
Właściwości DTFT
Linearity : $a_1x_1(n)+a_2x_2(n)\Leftrightarrow a_1X_1(e^{j\omega})+a_2X_2(e^{j\omega})$
Time shifting - $x(n-k)\Leftrightarrow e^{-j\omega k}.X(e^{j\omega})$
Time Reversal - $x(-n)\Leftrightarrow X(e^{-j\omega})$
Frequency shifting - $e^{j\omega _0n}x(n)\Leftrightarrow X(e^{j(\omega -\omega _0)})$
Differentiation frequency domain - $nx(n) = j\frac{d}{d\omega}X(e^{j\omega})$
Convolution - $x_1(n)*x_2(n)\Leftrightarrow X_1(e^{j\omega})\times X_2(e^{j\omega})$
Multiplication - $x_1(n)\times x_2(n)\Leftrightarrow X_1(e^{j\omega})*X_2(e^{j\omega})$
Co-relation - $y_{x_1\times x_2}(l)\Leftrightarrow X_1(e^{j\omega})\times X_2(e^{j\omega})$
Modulation theorem - $x(n)\cos \omega _0n = \frac{1}{2}[X_1(e^{j(\omega +\omega _0})*X_2(e^{jw})$
Symmetry -$x^*(n)\Leftrightarrow X^*(e^{-j\omega})$ ;
$x^*(-n)\Leftrightarrow X^*(e^{j\omega})$ ;
$Real[x(n)]\Leftrightarrow X_{even}(e^{j\omega})$ ;
$Imag[x(n)]\Leftrightarrow X_{odd}(e^{j\omega})$ ;
$x_{even}(n)\Leftrightarrow Real[x(e^{j\omega})]$ ;
$x_{odd}(n)\Leftrightarrow Imag[x(e^{j\omega})]$ ;
Parseval’s theorem - $\sum_{-\infty}^\infty|x_1(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X_1(e^{j\omega})|^2d\omega$
Wcześniej badaliśmy próbkowanie w dziedzinie częstotliwości. Mając tę podstawową wiedzę, próbujemy$X(e^{j\omega})$w dziedzinie częstotliwości, tak aby na podstawie próbkowanych danych można było przeprowadzić wygodną analizę cyfrową. W związku z tym DFT jest próbkowany zarówno w dziedzinie czasu, jak i częstotliwości. Z założeniem$x(n) = x_p(n)$
Stąd DFT jest wyrażone przez -
$X(k) = DFT[x(n)] = X(\frac{2\pi}{N}k) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{-\frac{j2\pi nk}{N}}$, k = 0,1,…., N − 1 … eq (3)
A IDFT jest określane przez -
$X(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k = 0}^{N-1}X(k)e^{\frac{j2\pi nk}{N}}$, n = 0,1,…., N − 1 … eq (4)
$\therefore x(n)\Leftrightarrow X(k)$
Twiddle Factor
Jest oznaczony jako $W_N$ i zdefiniowany jako $W_N = e^{-j2\pi /N}$. Jego wielkość jest zawsze utrzymywana w jedności. Faza$W_N = -2\pi /N$. Jest to wektor na okręgu jednostkowym i jest używany dla wygody obliczeń. Matematycznie można to przedstawić jako -
$W_N^r = W_N^{r\pm N} = W_N^{r\pm 2N} = ...$
Jest funkcją r i okresu N.
Rozważmy N = 8, r = 0,1,2,3,… .14,15,16,….
$\Longleftrightarrow W_8^0 = W_8^8 = W_8^{16} = ... = ... = W_8^{32} = ... =1= 1\angle 0$
$W_8^1 = W_8^9 = W_8^{17} = ... = ... = W_8^{33} = ... =\frac{1}{\sqrt 2}= j\frac{1}{\sqrt 2} = 1\angle-\frac{\pi}{4}$
Transformacja liniowa
Zrozummy transformację liniową -
Wiemy to,
$DFT(k) = DFT[x(n)] = X(\frac{2\pi}{N}k) = \sum_{n = 0}^{N-1}x(n).W_n^{-nk};\quad k = 0,1,….,N−1$
$x(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k = 0}^{N-1}X(k).W_N^{-nk};\quad n = 0,1,….,N−1$
Note- Obliczenie DFT można przeprowadzić stosując złożone mnożenie N 2 i dodawanie kompleksu N (N-1).
$x_N = \begin{bmatrix}x(0)\\x(1)\\.\\.\\x(N-1) \end{bmatrix}\quad N\quad point\quad vector\quad of\quad signal\quad x_N$
$X_N = \begin{bmatrix}X(0)\\X(1)\\.\\.\\X(N-1) \end{bmatrix}\quad N\quad point\quad vector\quad of\quad signal\quad X_N$
$\begin{bmatrix}1 & 1 & 1 & ... & ... & 1\\1 & W_N & W_N^2 & ... & ... & W_N^{N-1}\\. & W_N^2 & W_N^4 & ... & ... & W_N^{2(N-1)}\\.\\1 & W_N^{N-1} & W_N^{2(N-1)} & ... & ... & W_N^{(N-1)(N-1)} \end{bmatrix}$
N - punkt DFT w członie macierzy jest określony wzorem - $X_N = W_Nx_N$
$W_N\longmapsto$ Macierz transformacji liniowej
$Now,\quad x_N = W_N^{-1}X_N$
IDFT w postaci macierzy jest podany przez
$$x_N = \frac{1}{N}W_N^*X_N$$Porównanie obu wyrażeń $x_N,\quad W_N^{-1} = \frac{1}{N}W_N^*$ i $W_N\times W_N^* = N[I]_{N\times N}$
W związku z tym, $W_N$ jest liniową macierzą transformacji, macierzą ortogonalną (unitarną).
Z okresowej własności $W_N$ a z jej symetrycznej własności można wywnioskować, że $W_N^{k+N/2} = -W_N^k$
Symetria kołowa
N-punktowa DFT o skończonym czasie trwania x (n) długości N≤L, jest równoważna N-punktowej DFT okresowego wydłużenia x (n), tj. $x_p(n)$ okresu N. i $x_p(n) = \sum_{l = -\infty}^\infty x(n-Nl)$. Teraz, jeśli przesuniemy ciąg, który jest ciągiem okresowym o k jednostek w prawo, otrzymamy kolejny ciąg okresowy. Jest to znane jako przesunięcie okrężne i jest określone przez,
$$x_p^\prime (n) = x_p(n-k) = \sum_{l = -\infty}^\infty x(n-k-Nl)$$Nowy ciąg skończony można przedstawić jako
$$x_p^\prime (n) = \begin{cases}x_p^\prime(n), & 0\leq n\leq N-1\\0 & Otherwise\end{cases}$$Example - Niech x (n) = {1, 2, 4, 3}, N = 4,
$x_p^\prime (n) = x(n-k,modulo\quad N)\equiv x((n-k))_N\quad;ex-if\quad k=2i.e\quad 2\quad unit\quad right\quad shift\quad and\quad N = 4,$
Przyjęto kierunek zgodny z ruchem wskazówek zegara jako kierunek dodatni.
Mamy, $x\prime(n) = x((n-2))_4$
$x\prime(0) = x((-2))_4 = x(2) = 4$
$x\prime(1) = x((-1))_4 = x(3) = 3$
$x\prime(2) = x((-2))_4 = x(0) = 1$
$x\prime(3) = x((1))_4 = x(1) = 2$
Conclusion - Przesunięcie kołowe ciągu N-punktowego jest równoważne liniowemu przesunięciu jego okresowego wydłużenia i odwrotnie.
Cyklicznie równa sekwencja - $x(N-n) = x(n),\quad 1\leq n\leq N-1$
$i.e.x_p(n) = x_p(-n) = x_p(N-n)$
Koniugat parzysty -$x_p(n) = x_p^*(N-n)$
Cyklicznie nieparzysta sekwencja - $x(N-n) = -x(n),\quad 1\leq n\leq N-1$
$i.e.x_p(n) = -x_p(-n) = -x_p(N-n)$
Nieparzysty koniugat - $x_p(n) = -x_p^*(N-n)$
Teraz, $x_p(n) = x_{pe}+x_{po}(n)$, gdzie,
$x_{pe}(n) = \frac{1}{2}[x_p(n)+x_p^*(N-n)]$
$x_{po}(n) = \frac{1}{2}[x_p(n)-x_p^*(N-n)]$
Dla dowolnego rzeczywistego sygnału x (n),$X(k) = X^*(N-k)$
$X_R(k) = X_R(N-k)$
$X_l(k) = -X_l(N-k)$
$\angle X(k) = -\angle X(N-K)$
Time reversal- próbka odwrócona o próbce zerowej . Jest to podane jako;
$x((-n))_N = x(N-n),\quad 0\leq n\leq N-1$
Odwrócenie czasu to wykreślanie próbek sekwencji w kierunku zgodnym z ruchem wskazówek zegara, tj. Założonym kierunku ujemnym.
Niektóre inne ważne właściwości
Inne ważne właściwości IDFT $x(n)\longleftrightarrow X(k)$
Time reversal - $x((-n))_N = x(N-n)\longleftrightarrow X((-k))_N = X(N-k)$
Circular time shift - $x((n-l))_N \longleftrightarrow X(k)e^{j2\pi lk/N}$
Circular frequency shift - $x(n)e^{j2\pi ln/N} \longleftrightarrow X((k-l))_N$
Complex conjugate properties -
$x^*(n)\longleftrightarrow X^*((-k))_N = X^*(N-k)\quad and$
$x^*((-n))_N = x^*(N-n)\longleftrightarrow X^*(-k)$
Multiplication of two sequence -
$x_1(n)\longleftrightarrow X_1(k)\quad and\quad x_2(n)\longleftrightarrow X_2(k)$
$\therefore x_1(n)x_2(n)\longleftrightarrow X_1(k)\quadⓃ X_2(k)$
Circular convolution - i pomnożenie dwóch DFT
$x_1(k)\quad Ⓝ x_2(k) =\sum_{k = 0}^{N-1}x_1(n).x_2((m-n))_n,\quad m = 0,1,2,... .,N-1 $
$x_1(k)\quad Ⓝ x_2(k)\longleftrightarrow X_1(k).X_2(k)$
Circular correlation - Jeśli $x(n)\longleftrightarrow X(k)$ i $y(n)\longleftrightarrow Y(k)$ , to istnieje sekwencja korelacji krzyżowej oznaczona jako $\bar Y_{xy}$ takie że $\bar Y_{xy}(l) = \sum_{n = 0}^{N-1}x(n)y^*((n-l))_N = X(k).Y^*(k)$
Parseval’s Theorem - Jeśli $x(n)\longleftrightarrow X(k)$ i $y(n)\longleftrightarrow Y(k)$;
$\displaystyle\sum\limits_{n = 0}^{N-1}x(n)y^*(n) = \frac{1}{N}\displaystyle\sum\limits_{n =0}^{N-1}X(k).Y^*(k)$
Weźmy dwie sekwencje o skończonym czasie trwania x 1 (n) i x 2 (n), o długości całkowitej równej N. Ich DFT to odpowiednio X 1 (K) i X 2 (K), co pokazano poniżej -
$$X_1(K) = \sum_{n = 0}^{N-1}x_1(n)e^{\frac{j2\Pi kn}{N}}\quad k = 0,1,2...N-1$$ $$X_2(K) = \sum_{n = 0}^{N-1}x_2(n)e^{\frac{j2\Pi kn}{N}}\quad k = 0,1,2...N-1$$Teraz spróbujemy znaleźć DFT innej sekwencji x 3 (n), która jest podana jako X 3 (K)
$X_3(K) = X_1(K)\times X_2(K)$
Biorąc IDFT powyższego otrzymujemy
$x_3(n) = \frac{1}{N}\displaystyle\sum\limits_{n = 0}^{N-1}X_3(K)e^{\frac{j2\Pi kn}{N}}$
Po rozwiązaniu powyższego równania w końcu otrzymujemy
$x_3(n) = \displaystyle\sum\limits_{m = 0}^{N-1}x_1(m)x_2[((n-m))_N]\quad m = 0,1,2...N-1$
| Punkty porównawcze | Konwolucja liniowa | Okrągły splot |
|---|---|---|
| Przeniesienie | Przesunięcie liniowe | Przerzutki okrężne |
| Próbki w wyniku splotu | $N_1+N_2−1$ | $Max(N_1,N_2)$ |
| Znajdowanie odpowiedzi filtra | Możliwy | Możliwe z wypełnieniem zerowym |
Metody konwolucji kołowej
Ogólnie rzecz biorąc, istnieją dwie metody, które są przystosowane do wykonywania splotów kołowych i są to:
- Metoda koła koncentrycznego,
- Metoda mnożenia macierzy.
Metoda koła koncentrycznego
Pozwolić $x_1(n)$ i $x_2(n)$być dwiema podanymi sekwencjami. Kroki wykonane dla kołowego splotu$x_1(n)$ i $x_2(n)$ są
Weź dwa koncentryczne okręgi. Wykreśl N próbek z$x_1(n)$ na obwodzie koła zewnętrznego (z zachowaniem równych odległości kolejnych punktów) w kierunku przeciwnym do ruchu wskazówek zegara.
Do kreślenia $x_2(n)$, działka N próbek z $x_2(n)$w kierunku zgodnym z ruchem wskazówek zegara na wewnętrznym okręgu, rozpoczynając próbkę umieszczoną w tym samym punkcie co zerowa próbka$x_1(n)$
Pomnóż odpowiednie próbki w dwóch kółkach i dodaj je, aby uzyskać wynik.
Obracaj wewnętrzne koło w kierunku przeciwnym do ruchu wskazówek zegara z jedną próbką na raz.
Metoda mnożenia macierzy
Metoda macierzowa reprezentuje dwie podane sekwencje $x_1(n)$ i $x_2(n)$ w formie macierzy.
Jedna z podanych sekwencji jest powtarzana poprzez przesunięcie cykliczne jednej próbki na raz, aby utworzyć macierz NXN.
Druga sekwencja jest reprezentowana jako macierz kolumn.
Mnożenie dwóch macierzy daje wynik splotu kołowego.
DFT zapewnia alternatywne podejście do splotu w dziedzinie czasu. Może być używany do filtrowania liniowego w dziedzinie częstotliwości.
A zatem,$Y(\omega) = X(\omega).H(\omega)\longleftrightarrow y(n)$.
Problem w tym podejściu w dziedzinie częstotliwości polega na tym $Y(\omega)$, $X(\omega)$ i $H(\omega)$są ciągłą funkcją ω, która nie jest owocna dla obliczeń cyfrowych na komputerach. Jednak DFT zapewnia próbkowaną wersję tych przebiegów, aby rozwiązać ten cel.
Zaletą jest to, że mając wiedzę na temat szybszych technik DFT, takich jak FFT, można opracować bardziej wydajny obliczeniowo algorytm do cyfrowych obliczeń komputerowych w porównaniu z podejściem w dziedzinie czasu.
Rozważ sekwencję o skończonym czasie trwania, $[x(n) = 0,\quad for,n<0\quad and\quad n\geq L]$ (uogólnione równanie), wzbudza filtr liniowy z odpowiedzią impulsową $[h(n) = 0,\quad forn<0\quad and\quad n\geq M]$.
$$x(n)y(n)$$ $$output = y(n) = \sum_{k = 0}^{M-1}h(k).x(n-k)$$Z analizy splotu jasno wynika, że czas trwania y (n) wynosi L + M − 1.
W dziedzinie częstotliwości
$$Y(\omega) = X(\omega).H(\omega)$$Teraz, $Y(\omega)$ jest ciągłą funkcją ω i jest próbkowany na zbiorze dyskretnych częstotliwości z liczbą odrębnych próbek, które muszą być równe lub większe $L+M-1$.
$$DFT\quad size = N\geq L+M-1$$Z $\omega = \frac{2\pi}{N}k$,
$Y(\omega) = X(k).H(k)$, gdzie k = 0,1,…., N-1
Gdzie X (k) i H (k) to N-punktowe DFT odpowiednio x (n) i h (n). $x(n)\& h(n)$ są wypełnione zerami do długości N. Nie spowoduje to zniekształcenia ciągłych widm $X(\omega)$ i $H(\omega)$. Od$N\geq L+M-1$, N-punktowa DFT sekwencji wyjściowej y (n) jest wystarczająca, aby przedstawić y (n) w dziedzinie częstotliwości, a te fakty wskazują, że mnożenie N-punktowych DFT X (k) i H (k), po którym następuje obliczenie N-punktowej IDFT musi dać y (n).
Oznacza to, że N-punktowy splot kołowy x (n) i H (n) z wypełnieniem zerowym, jest równy splotowi liniowemu x (n) ih (n).
Zatem DFT może być używany do filtrowania liniowego.
Caution - N powinno zawsze być większe lub równe $L+M-1$. W przeciwnym razie efekt aliasingu spowodowałby uszkodzenie sekwencji wyjściowej.
Załóżmy, że sekwencja wejściowa x (n) o długim czasie trwania ma być przetworzona przez system o skończonej odpowiedzi impulsowej przez splot dwóch sekwencji. Ponieważ filtrowanie liniowe wykonywane przez DFT obejmuje działanie na bloku danych o stałej wielkości, sekwencja wejściowa jest dzielona na różne bloki danych o stałej wielkości przed przetwarzaniem.
Kolejne bloki są następnie przetwarzane pojedynczo, a wyniki są łączone w celu uzyskania wyniku netto.
Ponieważ splot jest wykonywany przez podzielenie długiej sekwencji wejściowej na różne sekcje o stałej wielkości, nazywa się to splotem sekcyjnym. Długa sekwencja wejściowa jest dzielona na bloki o stałej wielkości, przed przetwarzaniem filtra FIR.
Do oceny dyskretnego splotu stosowane są dwie metody -
Overlap-save method
Overlap-add method
Metoda zapisu nakładania się
Zachodzenie na siebie to tradycyjna nazwa wydajnego sposobu oceny dyskretnego splotu między bardzo długim sygnałem x (n) a filtrem h (n) o skończonej odpowiedzi impulsowej (FIR). Poniżej podano kroki metody zapisywania nakładania się -
Niech długość bloku danych wejściowych = N = L + M-1. Dlatego długość DFT i IDFT = N. Każdy blok danych przenosi M-1 punktów danych poprzedniego bloku, po których następuje L nowych punktów danych, tworząc sekwencję danych o długości N = L + M-1.
Najpierw obliczana jest N-punktowa DFT dla każdego bloku danych.
Dodając (L-1) zera, odpowiedź impulsowa filtra FIR jest zwiększana i obliczana i zapisywana jest N-punktowa DFT.
Mnożenie dwóch DFT punktów N H (k) i X m (k): Y ′ m (k) = H (k) .X m (k), gdzie K = 0,1,2,… N-1
Następnie IDFT [Y ′ m ((k)] = y ′ ((n) = [y ′ m (0), y ′ m (1), y ′ m (2), ....... y " m (m-1), Y" m (m), ....... r " m (n-1)]
(tutaj N-1 = L + M-2)
Pierwsze punkty M-1 są uszkodzone z powodu aliasingu i dlatego są odrzucane, ponieważ rekord danych ma długość N.
Ostatnie punkty L są dokładnie takie same jako wynik splotu, więc
y ′ m (n) = y m (n) gdzie n = M, M + 1,… .N-1
Aby uniknąć aliasingu, ostatnie elementy M-1 każdego rekordu danych są zapisywane i punkty te przenoszone są do następnego rekordu i stają się pierwszymi elementami M-1.

Wynik IDFT, w którym unika się pierwszych punktów M-1 w celu zniesienia aliasingu, a pozostałe punkty L stanowią pożądany wynik jako wynik splotu liniowego.
Metoda dodawania nakładania się
Poniżej podano kroki, aby znaleźć dyskretny splot przy użyciu metody Overlap -
Niech rozmiar bloku danych wejściowych będzie równy L. Dlatego rozmiar DFT i IDFT: N = L + M-1
Każdy blok danych jest uzupełniony zerami M-1 do ostatniego.
Oblicz N-punktową DFT.

Mnożone są dwa N-punktowe DFT: Y m (k) = H (k) .X m (k), gdzie k = 0,, 1,2,…., N-1
IDFT [Y m (k)] tworzy bloki o długości N, na które nie ma wpływu aliasowanie, ponieważ rozmiar DFT wynosi N = L + M-1 i zwiększono długości sekwencji do N-punktów przez dodanie M-1 zer do każdego blok.
Ostatnie punkty M-1 każdego bloku muszą być nałożone i dodane do pierwszych punktów M-1 kolejnego bloku.
(powód: każdy blok danych kończy się M-1 zerami)
Stąd ta metoda jest znana jako metoda dodawania nakładania się. W ten sposób otrzymujemy -
y (n) = {y 1 (0), y 1 (1), y 1 (2), ... .., y 1 (L-1), y 1 (L) + y 2 (0), y 1 (L + 1) + y 2 (1), ... ... .., y 1 (N-1) + y 2 (M-1), y 2 (M), ... .. . ... ... ...}
DCT (dyskretna transformata kosinusowa) to N-wejściowa sekwencja x (n), 0≤n≤N-1, jako transformacja liniowa lub kombinacja zespolonych wykładników. W rezultacie współczynniki DFT są na ogół złożone, nawet jeśli x (n) jest rzeczywiste.
Załóżmy, że próbujemy znaleźć ortogonalną transformację, która ma strukturę N × N, która wyraża rzeczywistą sekwencję x (n) jako liniową kombinację sekwencji kosinusowej. Już to wiemy -
$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)cos\frac{2\Pi kn}{N}0\leq k \leq N-1$
I $x(n) = \frac{1}{N}\sum_{k = 0}^{N-1}x(k)cos\frac{2\Pi kn}{N}0\leq k \leq N-1$
Jest to możliwe, jeśli sekwencja N punktów x (n) jest rzeczywista i parzysta. A zatem,$x(n) = x(N-n),0\leq n \leq (N-1)$. Wynikowy DFT jest rzeczywisty i równy. Te rzeczy jasno pokazują, że moglibyśmy prawdopodobnie wyznaczyć dyskretną transformatę kosinusową dla dowolnej N-punktowej sekwencji rzeczywistej, biorąc 2N punkt DFT „Parzystego rozszerzenia” sekwencji.
DCT jest zasadniczo używany w przetwarzaniu obrazu i mowy. Jest również używany do kompresji obrazów i sygnałów mowy.
$DFT[s(n)] = S(k) = \sum_{n = 0}^{2N-1}s(n)W_{2N}^{nk},\quad where\quad 0\leq k \leq 2N-1$
$S(k) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)W_{2N}^{nk}+\displaystyle\sum\limits_{n = N}^{2N-1}x(2N-n-1)W_{2N}^{nk};\quad where\quad 0\leq k\leq 2N-1$
$\Rightarrow S(k) = W_{2N}^{-k/2}+\sum_{n = 0}^{N-1}x(n) [W_{2N}^{nk}W_{2N}^{k/2}+W_{2N}^{-nk}W_{2N}^{-k/2}];\quad where\quad 0\leq k\leq 2N-1$
$\Rightarrow S(k) = W_{2N}^{\frac{k}{2}}\sum_{n = 0}^{N-1}x(n)\cos [\frac{\pi}{N}(n+\frac{1}{2})k];\quad where\quad 0\leq k\leq 2N-1$
DCT definiuje
$V(k) = 2\sum_{n = 0}^{N-1}x(n)\cos [\frac{\pi}{2}(n+\frac{1}{2})k]\quad where\quad 0\leq k\leq N-1$
$\Rightarrow V(k) = W_{2N}^{\frac{k}{2}}S(k)\quad or\quad S(k) = W_{2N}^{\frac{k}{2}}V(k),\quad where\quad 0\leq k\leq N-1$
$\Rightarrow V(k) = 2R[W_{2N}^{\frac{k}{2}}\sum_{n = 0}^{N-1}x(n)W_{2N}^{nk}],\quad where\quad 0\leq k\leq N-1$
Przykład 1
Sprawdź twierdzenie Parsevala o sekwencji $x(n) = \frac{1^n}{4}u(n)$
Solution - $\displaystyle\sum\limits_{-\infty}^\infty|x_1(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X_1(e^{j\omega})|^2d\omega$
LHS $\displaystyle\sum\limits_{-\infty}^\infty|x_1(n)|^2$
$= \displaystyle\sum\limits_{-\infty}^{\infty}x(n)x^*(n)$
$= \displaystyle\sum\limits_{-\infty}^\infty(\frac{1}{4})^{2n}u(n) = \frac{1}{1-\frac{1}{16}} = \frac{16}{15}$
RHS $X(e^{j\omega}) = \frac{1}{1-\frac{1}{4}e-j\omega} = \frac{1}{1-0.25\cos \omega+j0.25\sin \omega}$
$\Longleftrightarrow X^*(e^{j\omega}) = \frac{1}{1-0.25\cos \omega-j0.25\sin \omega}$
Obliczenie, $X(e^{j\omega}).X^*(e^{j\omega})$
$= \frac{1}{(1-0.25\cos \omega)^2+(0.25\sin \omega)^2} = \frac{1}{1.0625-0.5\cos \omega}$
$\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{1}{1.0625-0.5\cos \omega}d\omega$
$\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{1}{1.0625-0.5\cos \omega}d\omega = 16/15$
Widzimy, że LHS = RHS. (Stąd udowodniono)
Przykład 2
Oblicz N-punktową DFT z $x(n) = 3\delta (n)$
Solution - wiemy, że
$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{\frac{j2\Pi kn}{N}}$
$= \displaystyle\sum\limits_{n = 0}^{N-1}3\delta(n)e^{\frac{j2\Pi kn}{N}}$
$ = 3\delta (0)\times e^0 = 1$
Więc,$x(k) = 3,0\leq k\leq N-1$… Ans.
Przykład 3
Oblicz N-punktową DFT z $x(n) = 7(n-n_0)$
Solution - wiemy, że
$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{\frac{j2\Pi kn}{N}}$
Podstawiając wartość x (n),
$\displaystyle\sum\limits_{n = 0}^{N-1}7\delta (n-n_0)e^{-\frac{j2\Pi kn}{N}}$
$= e^{-kj14\Pi kn_0/N}$… Ans
We wcześniejszych metodach DFT widzieliśmy, że część obliczeniowa jest zbyt długa. Chcemy to zmniejszyć. Można to zrobić za pomocą FFT lub szybkiej transformaty Fouriera. Możemy więc powiedzieć, że FFT to nic innego jak obliczenie dyskretnej transformaty Fouriera w formacie algorytmicznym, w którym część obliczeniowa zostanie zredukowana.
Główną zaletą posiadania FFT jest to, że dzięki niemu możemy zaprojektować filtry FIR. Matematycznie FFT można zapisać następująco;
$$x[K] = \displaystyle\sum\limits_{n = 0}^{N-1}x[n]W_N^{nk}$$Weźmy przykład, aby lepiej to zrozumieć. Rozważaliśmy osiem punktów nazwanych z$x_0\quad to\quad x_7$. Wybierzemy parzyste terminy w jednej grupie, a nieparzyste w drugiej. Schematyczny widok powyższego pokazano poniżej -
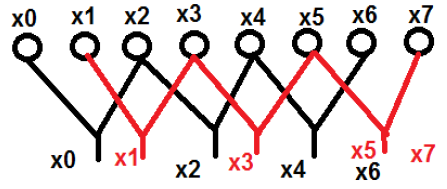
Tutaj punkty x 0 , x 2 , x 4 i x 6 zostały zgrupowane w jednej kategorii i podobnie punkty x 1 , x 3 , x 5 i x 7 zostały umieszczone w innej kategorii. Teraz możemy dalej tworzyć je w grupie dwóch i kontynuować obliczenia. Zobaczmy teraz, jak te rozdzielenie na kolejne dwie pomaga w obliczeniach.
$x[k] = \displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r]W_N^{2rk}+\displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_N^{(2r+1)k}$
$= \sum_{r = 0}^{\frac{N}{2}-1}x[2r]W_{N/2}^{rk}+\sum_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_{N/2}^{rk}\times W_N^k$
$= G[k]+H[k]\times W_N^k$
Początkowo wzięliśmy ośmiopunktową sekwencję, ale później podzieliliśmy ją na dwie części G [k] i H [k]. G [k] oznacza część parzystą, podczas gdy H [k] oznacza część nieparzystą. Jeśli chcemy to zrealizować za pomocą diagramu, można to pokazać jak poniżej -
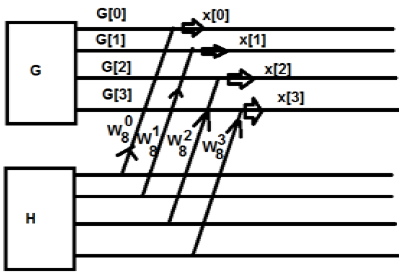
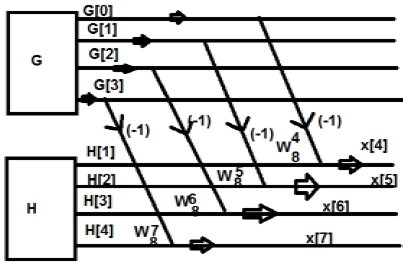
Widzimy to na powyższym rysunku
$W_8^4 = -1$
$W_8^5 = -W_8^1$
$W_8^6 = -W_8^2$
$W_8^7 = -W_8^3$
Podobnie końcowe wartości można zapisać w następujący sposób -
$G[0]-H[0] = x[4]$
$G[1]-W_8^1H[1] = x[5]$
$G[2]-W_8^2H[2] = x[6]$
$G[1]-W_8^3H[3] = x[7]$
Powyższy to cykl okresowy. Wadą tego systemu jest to, że K nie może zostać przełamane powyżej 4 punktów. Teraz podzielmy powyższe na dalsze. Otrzymamy takie struktury
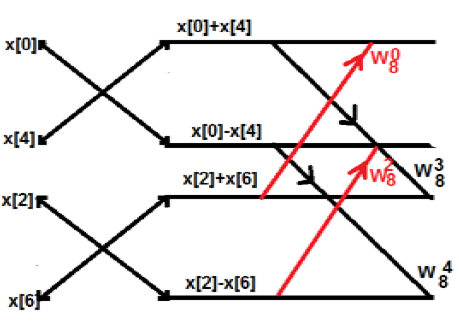
Przykład
Rozważmy ciąg x [n] = {2,1, -1, -3,0,1,2,1}. Oblicz FFT.
Solution - Podana sekwencja to x [n] = {2,1, -1, -3,0,1,2,1}
Ułóż terminy, jak pokazano poniżej;
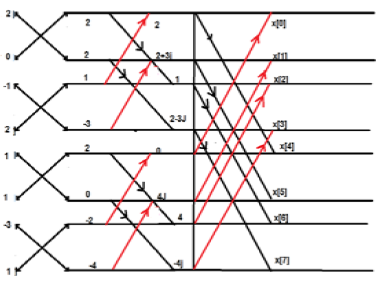
To wydajne wykorzystanie pamięci jest ważne przy projektowaniu szybkiego sprzętu do obliczania FFT. Termin „obliczenia w miejscu” jest używany do opisania tego użycia pamięci.
Dziesiątkowanie w ciągu czasowym
W tej strukturze wszystkie punkty przedstawiamy w formacie binarnym, czyli w 0 i 1. Następnie odwracamy te struktury. Sekwencja, którą otrzymujemy po tym, jest znana jako sekwencja odwrócenia bitów. Jest to również znane jako dziesiątkowanie sekwencji czasowej. Obliczenia w miejscu ośmiopunktowego DFT przedstawiono w formacie tabelarycznym, jak pokazano poniżej -
| ZWROTNICA | FORMAT BINARNY | ODWRÓCENIE | PUNKTY RÓWNOWAŻNE |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
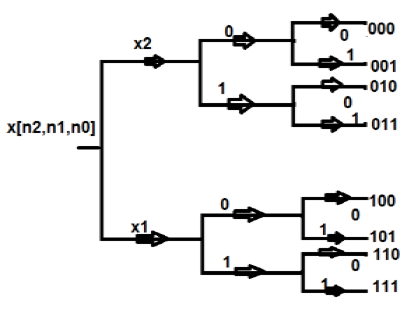
Decymacja w kolejności częstotliwości
Oprócz sekwencji czasowej sekwencja N-punktowa może być również reprezentowana częstotliwościowo. Weźmy czteropunktową sekwencję, aby lepiej to zrozumieć.
Niech kolejność będzie $x[0], x[1], x[2], x[3], x[4], x[5], x[6], x[7]$. Na początku zgrupujemy dwa punkty w jedną grupę. Matematycznie sekwencję tę można zapisać jako;
$$x[k] = \sum_{n = 0}^{N-1}x[n]W_N^{n-k}$$Zróbmy teraz jedną grupę sekwencji o numerach od 0 do 3 i drugą grupę o sekwencji od 4 do 7. Otóż, matematycznie można to przedstawić jako;
$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[n]W_N^{nk}+\displaystyle\sum\limits_{n = N/2}^{N-1}x[n]W_N^{nk}$$Zastąpmy n przez r, gdzie r = 0, 1, 2…. (N / 2-1). Matematycznie,
$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[r]W_{N/2}^{nr}$$Na początku bierzemy pierwsze cztery punkty (x [0], x [1], x [2], x [3]) i próbujemy przedstawić je matematycznie w następujący sposób -
$\sum_{n = 0}^3x[n]W_8^{nk}+\sum_{n = 0}^3x[n+4]W_8^{(n+4)k}$
$= \lbrace \sum_{n = 0}^3x[n]+\sum_{n = 0}^3x[n+4]W_8^{(4)k}\rbrace \times W_8^{nk}$
teraz $X[0] = \sum_{n = 0}^3(X[n]+X[n+4])$
$X[1] = \sum_{n = 0}^3(X[n]+X[n+4])W_8^{nk}$
$= [X[0]-X[4]+(X[1]-X[5])W_8^1+(X[2]-X[6])W_8^2+(X[3]-X[7])W_8^3$
Możemy dalej podzielić to na dwie kolejne części, co oznacza, że zamiast rozbijać je na sekwencje 4-punktowe, możemy je podzielić na sekwencje 2-punktowe.
Filtry FIR mogą być przydatne w tworzeniu wspomaganego komputerowo projektowania filtrów. Weźmy przykład i zobaczmy, jak to działa. Poniżej podano rysunek pożądanego filtra.

Projektując komputerowo, całe ciągłe wykresy dzielimy na dyskretne wartości. W pewnych granicach dzielimy to na 64, 256 lub 512 (i tak dalej) liczbę części o dyskretnych wielkościach.
W powyższym przykładzie przyjęliśmy granice między -π a + π. Podzieliliśmy go na 256 części. Punkty można przedstawić jako H (0), H (1),… aż do H (256). Tutaj stosujemy algorytm IDFT, a to da nam liniową charakterystykę fazową.
Czasami możemy być zainteresowani jakąś konkretną kolejnością filtrów. Powiedzmy, że chcemy zrealizować powyższy projekt przez filtr 9- go rzędu. Zatem przyjmujemy wartości filtrów jako h0, h1, h2… .h9. Matematycznie można to pokazać jak poniżej
$$H(e^{j\omega}) = h_0+h_1e^{-j\omega}+h_2e^{-2j\omega}+.....+h_9e^{-9j\omega}$$W przypadku dużej liczby zwichnięć otrzymujemy maksymalną liczbę punktów.
Na przykład na powyższym rysunku występuje nagły spadek nachylenia między punktami B i C. W tym momencie staramy się przyjąć bardziej dyskretne wartości, ale między punktem C i D. jest stałe nachylenie. mniejsza liczba wartości dyskretnych.
Aby zaprojektować powyższy filtr, przechodzimy przez proces minimalizacji w następujący sposób;
$H(e^{j\omega1}) = h_0+h_1e^{-j\omega1}+h_2e^{-2j\omega1}+.....+h_9e^{-9j\omega1}$
$H(e^{j\omega2}) = h_0+h_1e^{-j\omega2}+h_2e^{-2j\omega2}+.....+h_9e^{-9j\omega2}$
Podobnie,
$(e^{j\omega1000}) = h_0+h_1eH^{-j\omega1000}h_2e^{-2j\omega1000}+.....+h_9+e^{-9j\omega1000}$
Reprezentując powyższe równanie w postaci macierzowej, mamy -
$$\begin{bmatrix}H(e^{j\omega_1})\\.\\.\\H(e^{j\omega_{1000}}) \end{bmatrix} = \begin{bmatrix}e^{-j\omega_1} & ... & e^{-j9\omega_1} \\. & & . \\. & & . \\e^{-j\omega_{1000}} &... & e^{j9\omega_{1000}} \end{bmatrix}\begin{bmatrix}h_0\\.\\.\\h_9\end{bmatrix}$$Weźmy macierz 1000 × 1 jako B, macierz 1000 × 9 jako A, a macierz 9 × 1 jako $\hat{h}$.
Tak więc, aby rozwiązać powyższą macierz, napiszemy
$\hat{h} = [A^TA]^{-1}A^{T}B$
$= [A^{*T}A]^{-1}A^{*T}B$
gdzie A * reprezentuje złożony koniugat macierzy A.