DSP - Operacje na skalowaniu sygnałów
Skalowanie sygnału oznacza, że stała jest mnożona przez czas lub amplitudę sygnału.
Skalowanie czasu
Jeśli stała jest pomnożona do osi czasu, wtedy nazywa się to skalowaniem czasu. Można to matematycznie przedstawić jako;
$ x (t) \ rightarrow y (t) = x (\ alpha t) $ lub $ x (\ frac {t} {\ alpha}) $; gdzie α ≠ 0
Zatem oś y jest taka sama, wielkość osi x maleje lub rośnie zgodnie ze znakiem stałej (dodatniej lub ujemnej). Dlatego skalowanie można również podzielić na dwie kategorie, jak omówiono poniżej.
Kompresja czasu
Zawsze, gdy wartość alfa jest większa od zera, amplituda sygnału jest dzielona przez wartość alfa, podczas gdy wartość na osi Y pozostaje taka sama. Jest to znane jako kompresja czasu.
Example
Rozważmy sygnał x (t), który pokazano na poniższym rysunku. Przyjmijmy wartość alfa jako 2. Zatem y (t) będzie równe x (2t), co ilustruje podany rysunek.

Wyraźnie widać na powyższych rysunkach, że wielkość czasu na osi y pozostaje taka sama, ale amplituda na osi x zmniejsza się z 4 do 2. Jest to zatem przypadek kompresji czasu.
Rozszerzenie czasu
Gdy czas jest podzielony przez stałą wartość alfa, amplituda sygnału na osi Y zostaje pomnożona przez współczynnik alfa, co pozwala zachować wielkość osi X w niezmienionej postaci. Dlatego nazywa się to sygnałem typu rozszerzenie czasu.
Example
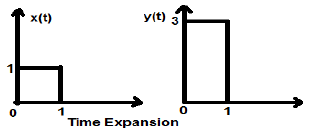
Rozważmy kwadratowy sygnał x (t) o wielkości 1. Kiedy przeskalujemy go w czasie przez stałą 3, tak że $ x (t) \ rightarrow y (t) \ rightarrow x (\ frac {t} {3} ) $, to amplituda sygnału jest modyfikowana trzykrotnie, co pokazano na poniższym rysunku.
Skalowanie amplitudy
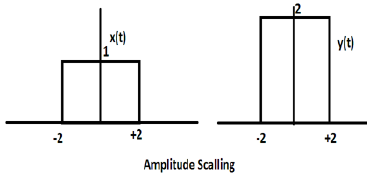
Mnożenie stałej przez amplitudę sygnału powoduje skalowanie amplitudy. W zależności od znaku stałej może to być skalowanie amplitudy lub tłumienie. Rozważmy sygnał prostokątny x (t) = Π (t / 4).
Załóżmy, że definiujemy inną funkcję y (t) = 2 Π (t / 4). W takim przypadku wartość osi y zostanie podwojona, zachowując wartość osi czasu bez zmian. Ilustruje to poniższy rysunek.
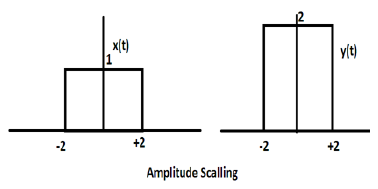
Rozważmy inną funkcję prostokątną zdefiniowaną jako z (t), gdzie z (t) = 0,5 Π (t / 4). Tutaj amplituda funkcji z (t) będzie równa połowie amplitudy x (t), tj. Oś czasu pozostanie taka sama, oś amplitudy zostanie zmniejszona o połowę. Ilustruje to poniższy rysunek.