DSP - Operacje na splotach sygnałów
Splot dwóch sygnałów w dziedzinie czasu jest równoznaczny z pomnożeniem ich reprezentacji w dziedzinie częstotliwości. Matematycznie możemy zapisać splot dwóch sygnałów jako
$$ y (t) = x_ {1} (t) * x_ {2} (t) $$ $$ = \ int _ {- \ infty} ^ {\ infty} x_ {1} (p) .x_ {2 } (tp) dp $$Kroki do splotu
- Weź sygnał x 1 (t) i umieść t = p tam, aby było x 1 (p).
- Weź sygnał x 2 (t) i wykonaj krok 1 i wykonaj x 2 (p).
- Zrób zwijanie sygnału, tj. X 2 (-p).
- Dokonaj przesunięcia w czasie powyższego sygnału x 2 [- (pt)]
- Następnie pomnóż oba sygnały. tj. $ x_ {1} (p) .x_ {2} [- (p − t)] $
Przykład
Zróbmy splot sygnału krokowego u (t) z jego własnym rodzajem.
$ y (t) = u (t) * u (t) $
$ = \ int _ {- \ infty} ^ {\ infty} [u (p) .u [- (pt)] dp $
Teraz to t może być większe lub mniejsze od zera, co pokazano na poniższych rysunkach
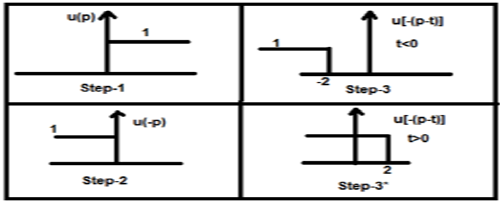
Tak więc w powyższym przypadku wynik powstaje z następującymi możliwościami
$ y (t) = \ begin {cases} 0, & if \ quad t <0 \\\ int_ {0} ^ {t} 1dt, & for \ quad t> 0 \ end {cases} $
$ = \ begin {cases} 0, & if \ quad t <0 \\ t, & t> 0 \ end {cases} = r (t) $
Właściwości splotu
Przemienne
Stwierdza, że kolejność splotów nie ma znaczenia, co można przedstawić matematycznie jako
$$ x_ {1} (t) * x_ {2} (t) = x_ {2} (t) * x_ {1} (t) $$Asocjacyjny
Stwierdza, że kolejność splotów obejmująca trzy sygnały może być dowolna. Matematycznie można to pokazać jako;
$$ x_ {1} (t) * [x_ {2} (t) * x_ {3} (t)] = [x_ {1} (t) * x_ {2} (t)] * x_ {3} (t) $$Dystrybucyjny
Najpierw można dodać dwa sygnały, a następnie wprowadzić ich splot do trzeciego sygnału. Jest to równoważne splotowi dwóch sygnałów indywidualnie z trzecim sygnałem i ostatecznie dodanym. Matematycznie można to zapisać jako;
$$ x_ {1} (t) * [x_ {2} (t) + x_ {3} (t)] = [x_ {1} (t) * x_ {2} (t) + x_ {1} ( t) * x_ {3} (t)] $$Powierzchnia
Jeśli sygnał jest wynikiem splotu dwóch sygnałów, obszar sygnału jest zwielokrotnieniem tych pojedynczych sygnałów. Matematycznie można to zapisać
Jeśli $ y (t) = x_ {1} * x_ {2} (t) $
Wtedy obszar y (t) = obszar x 1 (t) X obszar x 2 (t)
skalowanie
Jeśli dwa sygnały zostaną przeskalowane do jakiejś nieznanej stałej „a”, a splot zostanie wykonany, wynikowy sygnał również zostanie spleciony na tę samą stałą „a” i zostanie podzielony przez tę wielkość, jak pokazano poniżej.
Jeśli $ x_ {1} (t) * x_ {2} (t) = y (t) $
Następnie $ x_ {1} (at) * x_ {2} (at) = \ frac {y (at)} {a}, a \ ne 0 $
Opóźnienie
Załóżmy, że sygnał y (t) jest wynikiem splotu dwóch sygnałów x1 (t) i x2 (t). Jeżeli oba sygnały są opóźnione odpowiednio o czas t1 i t2, to wynikowy sygnał y (t) będzie opóźniony o (t1 + t2). Matematycznie można to zapisać jako -
Jeśli $ x_ {1} (t) * x_ {2} (t) = y (t) $
Następnie $ x_ {1} (t-t_ {1}) * x_ {2} (t-t_ {2}) = y [t- (t_ {1} + t_ {2})] $
Rozwiązane przykłady
Example 1 - Znajdź splot sygnałów u (t-1) i u (t-2).
Solution- Dane sygnały to u (t-1) iu (t-2). Ich splot można wykonać, jak pokazano poniżej -
$ y (t) = u (t-1) * u (t-2) $
$ y (t) = \ int _ {- \ infty} ^ {+ \ infty} [u (t-1) .u (t-2)] dt $
$ = r (t-1) + r (t-2) $
$ = r (t-3) $
Example 2 - Znajdź splot dwóch sygnałów podanych przez
$x_{1}(n) = \lbrace 3,-2, 2\rbrace $
$ x_ {2} (n) = \ begin {cases} 2, & 0 \ leq n \ leq 4 \\ 0, & x> gdzie indziej \ end {cases} $
Solution -
x 2 (n) można zdekodować jako $ x_ {2} (n) = \ lbrace 2,2,2,2,2 \ rbrace Originalfirst $
x 1 (n) podano wcześniej $ = \ lbrace 3, -2,3 \ rbrace = 3-2Z ^ {- 1} + 2Z ^ {- 2} $
Podobnie $ x_ {2} (z) = 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {- 4} $
Sygnał wynikowy,
$ X (Z) = X_ {1} (Z) X_ {2} (z) $
$ = \ lbrace 3-2Z ^ {- 1} + 2Z ^ {- 2} \ rbrace \ times \ lbrace 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {-4} \ rbrace $
$ = 6 + 2Z ^ {- 1} + 6Z ^ {- 2} + 6Z ^ {- 3} + 6Z ^ {- 4} + 6Z ^ {- 5} $
Biorąc pod uwagę odwrotną transformację Z powyższego, otrzymamy wynikowy sygnał jako
$ x (n) = \ lbrace 6,2,6,6,6,0,4 \ rbrace $ Początek na początku
Example 3 - Wyznacz splot kolejnych 2 sygnałów -
$x(n) = \lbrace 2,1,0,1\rbrace$
$h(n) = \lbrace 1,2,3,1\rbrace$
Solution -
Biorąc transformację Z sygnałów, otrzymujemy:
$ x (z) = 2 + 2Z ^ {- 1} + 2Z ^ {- 3} $
I $ h (n) = 1 + 2Z ^ {- 1} + 3Z ^ {- 2} + Z ^ {- 3} $
Teraz splot dwóch sygnałów oznacza zwielokrotnienie ich transformacji Z.
To jest $ Y (Z) = X (Z) \ razy h (Z) $
$ = \ lbrace 2 + 2Z ^ {- 1} + 2Z ^ {- 3} \ rbrace \ times \ lbrace 1 + 2Z ^ {- 1} + 3Z ^ {- 2} + Z ^ {- 3} \ rbrace $
$ = \ lbrace 2 + 5Z ^ {- 1} + 8Z ^ {- 2} + 6Z ^ {- 3} + 3Z ^ {- 4} + 3Z ^ {- 5} + Z ^ {- 6} \ rbrace $
Biorąc pod uwagę odwrotną transformację Z, wynikowy sygnał można zapisać jako;
$ y (n) = \ lbrace 2,5,8,6,6,1 \ rbrace Originalfirst $