DSP - Klasyfikacja sygnałów CT
Ciągłe sygnały czasu można sklasyfikować według różnych warunków lub operacji wykonywanych na sygnałach.
Sygnały parzyste i nieparzyste
Nawet sygnał
Mówi się, że sygnał jest, nawet jeśli spełnia następujący warunek;
$$ x (-t) = x (t) $$Odwrócenie czasu sygnału nie implikuje tutaj żadnej zmiany amplitudy. Weźmy na przykład pod uwagę trójkątną falę pokazaną poniżej.
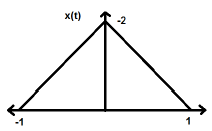
Sygnał trójkątny jest sygnałem parzystym. Ponieważ jest symetryczny względem osi Y. Można powiedzieć, że jest to odbicie lustrzane wokół osi Y.
Rozważ inny sygnał, jak pokazano na poniższym rysunku.
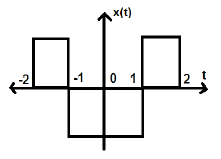
Widzimy, że powyższy sygnał jest równy symetrii względem osi Y.
Dziwny sygnał
Sygnał jest uważany za dziwny, jeśli spełnia następujący warunek
$$ x (-t) = -x (t) $$Tutaj odwrócenie czasu i zmiana amplitudy zachodzą jednocześnie.
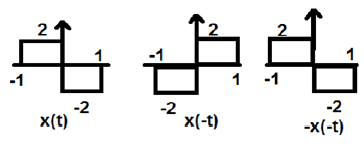
Na powyższym rysunku widzimy sygnał kroku x (t). Aby sprawdzić, czy jest to nieparzysty sygnał, najpierw wykonujemy odwrócenie czasu, tj. X (-t), a wynik jest taki, jak pokazano na rysunku. Następnie odwracamy amplitudę sygnału wypadkowego czyli –x (-t) i otrzymujemy wynik jak na rysunku.
Jeśli porównamy pierwszy i trzeci przebieg, zobaczymy, że są one takie same, tj. X (t) = -x (-t), co spełnia nasze kryteria. Dlatego powyższy sygnał jest sygnałem Odd.
Poniżej przedstawiono kilka ważnych wyników dotyczących sygnałów parzystych i nieparzystych.
- Parzyste × Parzyste = Parzyste
- Nieparzyste × Nieparzyste = Parzyste
- Parzyste × Nieparzyste = Nieparzyste
- Parzysty ± Parzysty = Parzysty
- Nieparzyste ± Nieparzyste = Nieparzyste
- Parzyste ± Nieparzyste = Ani parzyste, ani nieparzyste
Reprezentacja dowolnego sygnału w formie parzystej lub nieparzystej
Niektórych sygnałów nie można bezpośrednio sklasyfikować jako parzyste lub nieparzyste. Są one reprezentowane jako połączenie parzystego i nieparzystego sygnału.
$$ x (t) \ rightarrow x_ {e} (t) + x_ {0} (t) $$Gdzie x e (t) reprezentuje sygnał parzysty, a x o (t) reprezentuje sygnał nieparzysty
$$ x_ {e} (t) = \ frac {[x (t) + x (-t)]} {2} $$I
$$ x_ {0} (t) = \ frac {[x (t) -x (-t)]} {2} $$Przykład
Znajdź parzyste i nieparzyste części sygnału $ x (n) = t + t ^ {2} + t ^ {3} $
Solution - Z odwrócenia x (n), otrzymujemy
$$ x (-n) = -t + t ^ {2} -t ^ {3} $$
Teraz, zgodnie ze wzorem, część parzysta
$$ x_ {e} (t) = \ frac {x (t) + x (-t)} {2} $$
$$ = \ frac {[(t + t ^ {2} + t ^ {3}) + (- t + t ^ {2} -t ^ {3})]} {2} $$
$$ = t ^ {2} $$
Podobnie, zgodnie ze wzorem, część nieparzysta jest
$$ x_ {0} (t) = \ frac {[x (t) -x (-t)]} {2} $$
$$ = \ frac {[(t + t ^ {2} + t ^ {3}) - (- t + t ^ {2} -t ^ {3})]} {2} $$
$$ = t + t ^ {3} $$
Sygnały okresowe i nieokresowe
Sygnały okresowe
Okresowy sygnał powtarza się po pewnym czasie. Możemy to pokazać w formie równania jako -
$$ x (t) = x (t) \ pm nT $$Gdzie, n = liczba całkowita (1, 2, 3…)
T = podstawowy okres czasu (FTP) ≠ 0 i ≠ ∞
Podstawowy okres czasu (FTP) to najmniejsza dodatnia i stała wartość czasu, dla którego sygnał jest okresowy.
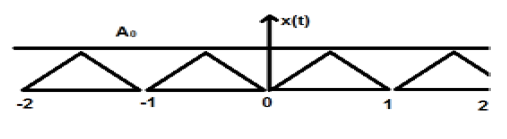
Na powyższym rysunku przedstawiono trójkątny sygnał o amplitudzie A. Tutaj sygnał powtarza się co 1 sek. Dlatego można powiedzieć, że sygnał jest okresowy, a jego współczynnik FTP wynosi 1 sek.
Sygnał nieokresowy
Po prostu można powiedzieć, że sygnały, które nie są okresowe, mają charakter nieokresowy. Jak oczywiste, sygnały te nie będą się powtarzać po jakimkolwiek czasie.
Sygnały nieokresowe nie mają określonego formatu; dlatego żadne konkretne równanie matematyczne nie może ich opisać.
Sygnały energii i mocy
Mówi się, że sygnał jest sygnałem energii, wtedy i tylko wtedy, gdy całkowita zawarta w nim energia jest skończona i niezerowa (0 <E <∞). Dlatego dla dowolnego sygnału typu energii całkowity znormalizowany sygnał jest skończony i niezerowy.
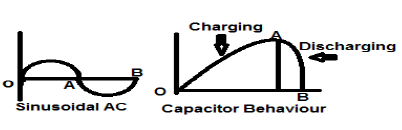
Sinusoidalny sygnał prądu przemiennego jest doskonałym przykładem sygnału typu Energia, ponieważ w jednym przypadku jest w dodatnim półcyklu, a następnie jest ujemny w następnym półcyklu. Dlatego jego średnia moc wynosi zero.
Bezstratny kondensator jest również doskonałym przykładem sygnału typu Energy, ponieważ po podłączeniu do źródła ładuje się do optymalnego poziomu, a po usunięciu źródła rozprasza tę równą ilość energii przez obciążenie i sprawia, że jego średnia moc zero.
Dla każdego skończonego sygnału x (t) energia może być symbolizowana jako E i zapisywana jako;
$$ E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt $$Gęstość widmowa sygnałów typu energii określa ilość energii rozprowadzanej na różnych poziomach częstotliwości.
Sygnały typu mocy
Mówi się, że sygnał jest sygnałem typu mocy, wtedy i tylko wtedy, gdy znormalizowana moc średnia jest skończona i niezerowa, tj. (0 <p <∞). Dla sygnału typu mocy znormalizowana średnia moc jest skończona i niezerowa. Prawie wszystkie sygnały okresowe są sygnałami mocy, a ich średnia moc jest skończona i niezerowa.
W formie matematycznej moc sygnału x (t) można zapisać jako;
$$ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt $$Różnica między sygnałami energii i mocy
Poniższa tabela podsumowuje różnice sygnałów energii i mocy.
| Sygnał mocy | Sygnał energii |
|---|---|
| Praktyczne sygnały okresowe są sygnałami mocy. | Sygnały nieokresowe to sygnały energii. |
| Tutaj znormalizowana średnia moc jest skończona i niezerowa. | Tutaj całkowita znormalizowana energia jest skończona i niezerowa. |
| Matematycznie, $$ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt $$ |
Matematycznie, $$ E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt $$ |
| Istnienie tych sygnałów jest nieskończone w czasie. | Sygnały te istnieją przez ograniczony czas. |
| Energia sygnału mocy jest nieskończona w nieskończonym czasie. | Moc sygnału energii wynosi zero w nieskończonym czasie. |
Rozwiązane przykłady
Example 1 - Znajdź moc sygnału $ z (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) + 4 \ sin (3 \ Pi + 30 ^ {o}) $
Solution- Powyższe dwa sygnały są względem siebie ortogonalne, ponieważ ich składniki częstotliwości są identyczne, a także mają taką samą różnicę faz. Zatem całkowita moc będzie sumą indywidualnych mocy.
Niech $ z (t) = x (t) + y (t) $
Gdzie $ x (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) $ i $ y (t) = 4 \ sin (3 \ Pi + 30 ^ {o}) $
Potęga $ x (t) = \ frac {2 ^ {2}} {2} = 2 $
Potęga $ y (t) = \ frac {4 ^ {2}} {2} = 8 $
Dlatego $ P (z) = p (x) + p (y) = 2 + 8 = 10 $ … Ans.
Example 2 - Sprawdź, czy dany sygnał $ x (t) = t ^ {2} + j \ sin t $ jest sprzężony, czy nie?
Solution- Tutaj część rzeczywista będąca t 2 jest parzysta, a część nieparzysta (urojona) będąca $ \ sin t $ jest nieparzysta. Więc powyższy sygnał jest sygnałem sprzężonym.
Example 3 - Sprawdź, czy $ X (t) = \ sin \ omega t $ jest sygnałem nieparzystym, czy parzystym.
Solution - Biorąc pod uwagę $ X (t) = \ sin \ omega t $
Do odwrócenia czasu otrzymamy $ \ sin (- \ omega t) $
Ale wiemy, że $ \ sin (- \ phi) = - \ sin \ phi $.
W związku z tym,
$$ \ sin (- \ omega t) = - \ sin \ omega t $$To spełnia warunek, aby sygnał był nieparzysty. Dlatego $ \ sin \ omega t $ jest nieparzystym sygnałem.