Cyfrowe przetwarzanie sygnału - definicja sygnałów

Definicja

Wszystko, co przenosi informacje, można nazwać sygnałem. Można go również zdefiniować jako wielkość fizyczną, która zmienia się wraz z czasem, temperaturą, ciśnieniem lub dowolnymi zmiennymi niezależnymi, takimi jak sygnał mowy lub sygnał wideo.

Proces działania, w którym właściwości sygnału (amplituda, kształt, faza, częstotliwość itp.) Ulegają zmianie, nazywamy przetwarzaniem sygnału.

Note- Każdy niechciany sygnał zakłócający główny sygnał nazywany jest szumem. Zatem szum jest również sygnałem, ale niepożądany.

Zgodnie z ich reprezentacją i przetwarzaniem sygnały można podzielić na różne kategorie, których szczegóły omówiono poniżej.

Ciągłe sygnały czasu

Sygnały czasu ciągłego są definiowane wzdłuż kontinuum czasu i dlatego są reprezentowane przez ciągłą zmienną niezależną. Sygnały czasu ciągłego są często określane jako sygnały analogowe.

Ten typ sygnału wykazuje ciągłość zarówno pod względem amplitudy, jak i czasu. Będą one miały wartości w każdej chwili. Funkcje sinus i cosinus są najlepszym przykładem ciągłego sygnału czasu.

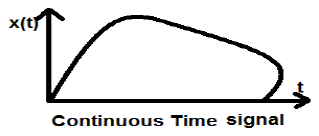
Sygnał pokazany powyżej jest przykładem ciągłego sygnału czasu, ponieważ możemy uzyskać wartość sygnału w każdej chwili.

Sygnały czasu dyskretnego

Sygnały, które są definiowane dyskretnie, nazywane są sygnałami dyskretnymi. Dlatego każda zmienna niezależna ma odrębną wartość. W ten sposób są przedstawiane jako sekwencje liczb.

Chociaż sygnały mowy i wideo mają przywilej reprezentowania zarówno w formacie ciągłym, jak i dyskretnym; w pewnych okolicznościach są identyczne. Amplitudy również wykazują charakterystykę dyskretną. Doskonałym tego przykładem jest sygnał cyfrowy; których amplituda i czas są dyskretne.

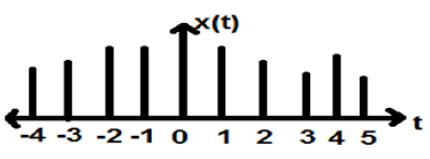
Powyższy rysunek przedstawia dyskretną charakterystykę amplitudy sygnału dyskretnego w okresie czasu. Matematycznie te typy sygnałów można sformułować jako;

$$ x = \ left \ {x \ left [n \ right] \ right \}, \ quad - \ infty <n <\ infty $$

Gdzie n jest liczbą całkowitą.

Jest to ciąg liczb x, gdzie n- ^ta liczba w ciągu jest reprezentowana jako x [n].