Cyfrowe przetwarzanie sygnału - podstawowe sygnały CT

Do testowania systemu stosuje się zwykle sygnały standardowe lub podstawowe. Sygnały te są podstawowymi elementami budulcowymi wielu złożonych sygnałów. Dlatego odgrywają bardzo ważną rolę w badaniu sygnałów i systemów.

Jednostkowy impuls lub funkcja delta

Sygnał, który spełnia warunek, $ \ delta (t) = \ lim _ {\ epsilon \ to \ infty} x (t) $ jest nazywany jednostkowym sygnałem impulsowym. Sygnał ten dąży do nieskończoności, gdy t = 0 i dąży do zera, gdy t ≠ 0, tak że obszar pod jego krzywą jest zawsze równy jeden. Funkcja delta ma wszędzie zerową amplitudę excunit_impulse.jpgept przy t = 0.

Właściwości jednostkowego sygnału impulsowego

• δ (t) jest sygnałem parzystym.
• δ (t) nie jest przykładem sygnału ani energii, ani mocy (NENP).
• Obszar jednostkowego sygnału impulsowego można zapisać jako;
$$ A = \ int _ {- \ infty} ^ {\ infty} \ delta (t) dt = \ int _ {- \ infty} ^ {\ infty} \ lim _ {\ epsilon \ to 0} x (t) dt = \ lim _ {\ epsilon \ to 0} \ int _ {- \ infty} ^ {\ infty} [x (t) dt] = 1 $$
• Wagę lub siłę sygnału można zapisać jako;
$$ y (t) = A \ delta (t) $$
• Obszar ważonego sygnału impulsowego można zapisać jako -
$$ y (t) = \ int _ {- \ infty} ^ {\ infty} y (t) dt = \ int _ {- \ infty} ^ {\ infty} A \ delta (t) = A [\ int _ {- \ infty} ^ {\ infty} \ delta (t) dt] = A = 1 = Wigthedimpulse $$

Sygnał kroku jednostki

Sygnał spełniający dwa następujące warunki -

• $ U (t) = 1 (gdy \ quad t \ geq 0) i $
• $ U (t) = 0 (gdy \ quad t <0) $

jest znany jako sygnał kroku jednostkowego.

Ma właściwość pokazywania nieciągłości w momencie t = 0. W punkcie nieciągłości wartość sygnału jest podana jako średnia wartości sygnału. Sygnał ten został pobrany tuż przed i po punkcie nieciągłości (według Zjawisk Gibba).

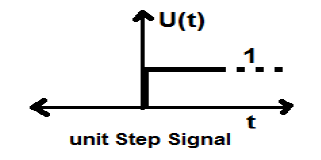
Jeśli dodamy sygnał kroku do innego sygnału kroku, który jest skalowany w czasie, wynikiem będzie jedność. Jest to sygnał typu mocy, a wartość mocy wynosi 0,5. Wartość RMS (Root mean square) wynosi 0,707, a jej średnia wartość również wynosi 0,5

Sygnał rampy

Całkowanie sygnału kroku daje w wyniku sygnał Ramp. Jest reprezentowany przez r (t). Sygnał rampy spełnia również warunek $ r (t) = \ int _ {- \ infty} ^ {t} U (t) dt = tU (t) $. Nie jest to sygnał typu energii ani mocy (NENP).

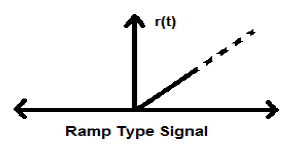
Sygnał paraboliczny

Całkowanie sygnału Ramp prowadzi do sygnału parabolicznego. Jest reprezentowany przez p (t). Sygnał paraboliczny spełnia również warunek $ p (t) = \ int _ {- \ infty} ^ {t} r (t) dt = (t ^ {2} / 2) U (t) $. Nie jest to sygnał typu energii ani mocy (NENP).

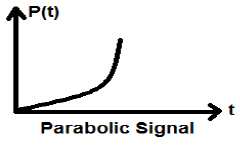
Funkcja Signum

Ta funkcja jest reprezentowana jako

$$ sgn (t) = \ begin {cases} 1 & for \ quad t> 0 \\ - 1 & for \ quad t <0 \ end {cases} $$

Jest to sygnał typu mocy. Jego wartość mocy i wartości RMS (średnia kwadratowa) wynoszą 1. Średnia wartość funkcji signum wynosi zero.

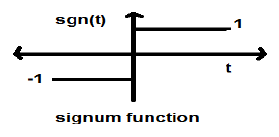
Funkcja Sinc

Jest to również funkcja sinusa i jest zapisywane jako -

$$ SinC (t) = \ frac {Sin \ Pi t} {\ Pi T} = Sa (\ Pi t) $$

Właściwości funkcji Sinc

• Jest to sygnał typu energetycznego.

• $ Sinc (0) = \ lim_ {t \ to 0} \ frac {\ sin \ Pi t} {\ Pi t} = 1 $

• $ Sinc (\ infty) = \ lim_ {t \ to \ infty} \ frac {\ sin \ Pi \ infty} {\ Pi \ infty} = 0 $ (Zakres sinπ∞ waha się od -1 do +1, ale wszystko jest podzielone przez nieskończoność równa się zero)

• Jeśli $ \ sin c (t) = 0 => \ sin \ Pi t = 0 $

  $ \ Rightarrow \ Pi t = n \ Pi $

  $ \ Rightarrow t = n (n \ neq 0) $

Sygnał sinusoidalny

Sygnał o charakterze ciągłym nazywany jest sygnałem ciągłym. Ogólny format sygnału sinusoidalnego to

$$ x (t) = A \ sin (\ omega t + \ phi) $$

Tutaj,

A = amplituda sygnału

ω = częstotliwość kątowa sygnału (mierzona w radianach)

φ = kąt fazowy sygnału (mierzony w radianach)

Ten sygnał ma tendencję do powtarzania się po pewnym czasie, dlatego nazywany jest sygnałem okresowym. Okres czasu sygnału jest podany jako;

$$ T = \ frac {2 \ pi} {\ omega} $$

Schematyczny widok sygnału sinusoidalnego pokazano poniżej.

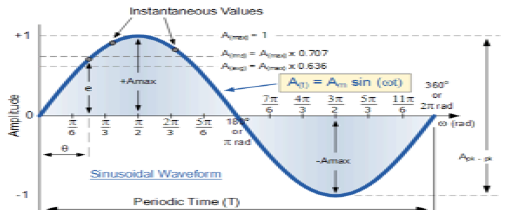
Funkcja prostokątna

Mówi się, że sygnał jest prostokątnym typem funkcji, jeśli spełnia następujący warunek -

$$ \ pi (\ frac {t} {\ tau}) = \ begin {cases} 1, & for \ quad t \ leq \ frac {\ tau} {2} \\ 0, & Otherwise \ end {cases} $$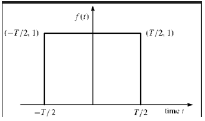

Ponieważ sygnał ten jest symetryczny względem osi Y, nazywany jest sygnałem parzystym.

Trójkątny sygnał impulsowy

Każdy sygnał, który spełnia następujący warunek, nazywany jest sygnałem trójkątnym.

$$ \ Delta (\ frac {t} {\ tau}) = \ begin {cases} 1 - (\ frac {2 | t |} {\ tau}) & for | t | <\ frac {\ tau} { 2} \\ 0 & for | t |> \ frac {\ tau} {2} \ end {cases} $$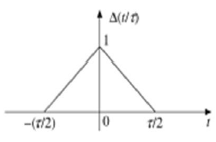

Ten sygnał jest symetryczny względem osi Y. Dlatego jest również określany jako sygnał równy.