การประมวลผลสัญญาณดิจิทัล - คู่มือฉบับย่อ

คำจำกัดความ

สิ่งใดก็ตามที่มีข้อมูลสามารถเรียกได้ว่าเป็นสัญญาณ นอกจากนี้ยังสามารถกำหนดเป็นปริมาณทางกายภาพที่แตกต่างกันไปตามเวลาอุณหภูมิความดันหรือตัวแปรอิสระเช่นสัญญาณเสียงพูดหรือสัญญาณวิดีโอ

กระบวนการทำงานที่ลักษณะของสัญญาณ (แอมพลิจูดรูปร่างเฟสความถี่ ฯลฯ ) มีการเปลี่ยนแปลงเรียกว่าการประมวลผลสัญญาณ

Note- สัญญาณที่ไม่ต้องการรบกวนสัญญาณหลักเรียกว่าสัญญาณรบกวน ดังนั้นสัญญาณรบกวนก็เป็นสัญญาณเช่นกัน แต่ไม่ต้องการ

ตามการนำเสนอและการประมวลผลสัญญาณสามารถแบ่งออกเป็นหมวดหมู่ต่างๆโดยละเอียดซึ่งจะกล่าวถึงด้านล่าง

สัญญาณเวลาต่อเนื่อง

สัญญาณเวลาต่อเนื่องถูกกำหนดตามช่วงเวลาต่อเนื่องและแสดงด้วยตัวแปรอิสระต่อเนื่อง สัญญาณเวลาต่อเนื่องมักเรียกว่าสัญญาณอนาล็อก

สัญญาณประเภทนี้แสดงความต่อเนื่องทั้งในแอมพลิจูดและเวลา สิ่งเหล่านี้จะมีค่าในแต่ละช่วงเวลา ฟังก์ชันไซน์และโคไซน์เป็นตัวอย่างที่ดีที่สุดของสัญญาณบอกเวลาต่อเนื่อง

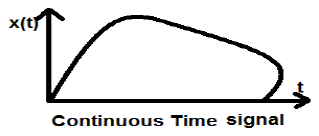
สัญญาณที่แสดงด้านบนเป็นตัวอย่างของสัญญาณเวลาต่อเนื่องเนื่องจากเราสามารถรับค่าของสัญญาณได้ในแต่ละช่วงเวลา

สัญญาณเวลาไม่ต่อเนื่อง

สัญญาณซึ่งกำหนดในเวลาที่ไม่ต่อเนื่องเรียกว่าสัญญาณไม่ต่อเนื่อง ดังนั้นตัวแปรอิสระทุกตัวจึงมีค่าที่แตกต่างกัน ดังนั้นจึงแสดงเป็นลำดับของตัวเลข

แม้ว่าสัญญาณเสียงพูดและวิดีโอจะมีสิทธิพิเศษในการแสดงทั้งในรูปแบบเวลาต่อเนื่องและไม่ต่อเนื่อง ภายใต้สถานการณ์บางอย่างมันเหมือนกัน แอมพลิจูดยังแสดงลักษณะที่ไม่ต่อเนื่อง ตัวอย่างที่สมบูรณ์แบบคือสัญญาณดิจิตอล ซึ่งแอมพลิจูดและเวลาทั้งสองไม่ต่อเนื่อง

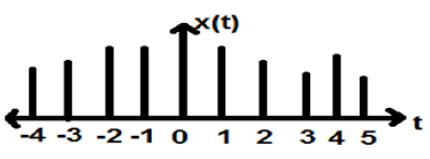
รูปด้านบนแสดงลักษณะแอมพลิจูดแบบไม่ต่อเนื่องของสัญญาณที่ไม่ต่อเนื่องในช่วงเวลาหนึ่ง ในทางคณิตศาสตร์สัญญาณประเภทนี้สามารถจัดรูปแบบเป็น;

$$x = \left \{ x\left [ n \right ] \right \},\quad -\infty < n< \infty$$

โดยที่nคือจำนวนเต็ม

มันเป็นลำดับของตัวเลข x ที่ n ^THตัวเลขในลำดับจะแสดงเป็น x [N]

ในการทดสอบระบบโดยทั่วไปจะใช้สัญญาณมาตรฐานหรือสัญญาณพื้นฐาน สัญญาณเหล่านี้เป็นส่วนประกอบพื้นฐานสำหรับสัญญาณที่ซับซ้อนจำนวนมาก ดังนั้นจึงมีบทบาทสำคัญมากในการศึกษาสัญญาณและระบบ

Unit Impulse หรือ Delta Function

สัญญาณที่ตรงตามเงื่อนไข $\delta(t) = \lim_{\epsilon \to \infty} x(t)$เรียกว่าสัญญาณอิมพัลส์ของหน่วย สัญญาณนี้มีแนวโน้มที่จะไม่มีที่สิ้นสุดเมื่อ t = 0 และมีแนวโน้มที่จะเป็นศูนย์เมื่อ t ≠ 0 เช่นนั้นพื้นที่ใต้เส้นโค้งจะเท่ากับหนึ่งเสมอ ฟังก์ชันเดลต้ามีแอมพลิจูดเป็นศูนย์ทุกที่ excunit_impulse.jpgept ที่ t = 0

คุณสมบัติของสัญญาณอิมพัลส์ยูนิต

δ (t) เป็นสัญญาณคู่
δ (t) เป็นตัวอย่างของสัญญาณพลังงานหรือพลังงาน (NENP)
พื้นที่ของสัญญาณอิมพัลส์ของหน่วยสามารถเขียนเป็น;
น้ำหนักหรือความแรงของสัญญาณสามารถเขียนเป็น;
พื้นที่ของสัญญาณอิมพัลส์ถ่วงน้ำหนักสามารถเขียนเป็น -

สัญญาณขั้นตอนของหน่วย

สัญญาณซึ่งเป็นไปตามเงื่อนไขสองข้อต่อไปนี้ -

$U(t) = 1(when\quad t \geq 0 )and$
$U(t) = 0 (when\quad t < 0 )$

เรียกว่าสัญญาณขั้นตอนของหน่วย

มีคุณสมบัติในการแสดงความไม่ต่อเนื่องที่ t = 0 ณ จุดที่ไม่ต่อเนื่องค่าสัญญาณจะถูกกำหนดโดยค่าเฉลี่ยของค่าสัญญาณ สัญญาณนี้เกิดขึ้นก่อนและหลังจุดที่ไม่ต่อเนื่อง (ตามปรากฏการณ์ของกิบบ์)

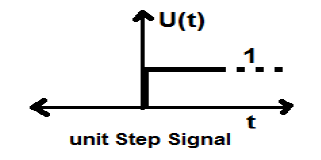
หากเราเพิ่มสัญญาณขั้นตอนลงในสัญญาณขั้นตอนอื่นที่มีการปรับขนาดเวลาผลลัพธ์จะเป็นเอกภาพ เป็นสัญญาณประเภทกำลังและค่าของกำลัง 0.5 ค่า RMS (รูทเฉลี่ยกำลังสอง) คือ 0.707 และค่าเฉลี่ยคือ 0.5

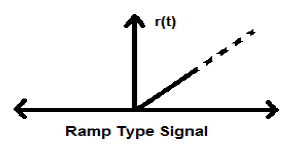
สัญญาณทางลาด

การรวมสัญญาณขั้นตอนส่งผลให้เกิดสัญญาณทางลาด มันแสดงด้วย r (t) สัญญาณทางลาดยังเป็นไปตามเงื่อนไข$r(t) = \int_{-\infty}^{t} U(t)dt = tU(t)$. ไม่ใช่สัญญาณประเภทพลังงานหรือพลังงาน (NENP)

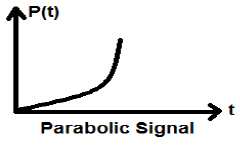
สัญญาณพาราโบลา

การรวมสัญญาณ Ramp นำไปสู่สัญญาณพาราโบลา มันแสดงด้วย p (t) สัญญาณพาราโบลายังเป็นไปตามเงื่อนไขของเขา$p(t) = \int_{-\infty}^{t} r(t)dt = (t^{2}/2)U(t)$. ไม่ใช่สัญญาณประเภทพลังงานหรือพลังงาน (NENP)

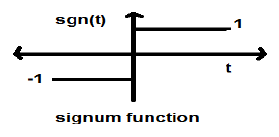
ฟังก์ชัน Signum

ฟังก์ชันนี้แสดงเป็น

$$sgn(t) = \begin{cases}1 & for\quad t >0\\-1 & for\quad t<0\end{cases}$$

มันเป็นสัญญาณประเภทพลังงาน ค่ากำลังและค่า RMS (ค่าเฉลี่ยกำลังสอง) ทั้งสองคือ 1 ค่าเฉลี่ยของฟังก์ชันเครื่องหมายเป็นศูนย์

ฟังก์ชัน Sinc

นอกจากนี้ยังเป็นฟังก์ชันของไซน์และเขียนเป็น -

$$SinC(t) = \frac{Sin\Pi t}{\Pi T} = Sa(\Pi t)$$

คุณสมบัติของฟังก์ชัน Sinc

มันเป็นสัญญาณประเภทพลังงาน
$Sinc(0) = \lim_{t \to 0}\frac{\sin \Pi t}{\Pi t} = 1$
$Sinc(\infty) = \lim_{t \to \infty}\frac{\sin \Pi \infty}{\Pi \infty} = 0$ (ช่วงของsinπ∞แตกต่างกันไประหว่าง -1 ถึง +1 แต่อะไรก็ตามที่หารด้วยอินฟินิตี้จะเท่ากับศูนย์)
ถ้า $ \sin c(t) = 0 => \sin \Pi t = 0$

$\Rightarrow \Pi t = n\Pi$

$\Rightarrow t = n (n \neq 0)$

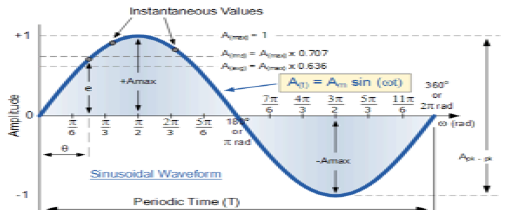
สัญญาณไซน์

สัญญาณซึ่งมีลักษณะต่อเนื่องเรียกว่าสัญญาณต่อเนื่อง รูปแบบทั่วไปของสัญญาณไซน์คือ

$$x(t) = A\sin (\omega t + \phi )$$

ที่นี่

A = แอมพลิจูดของสัญญาณ

ω = ความถี่เชิงมุมของสัญญาณ (วัดเป็นเรเดียน)

φ = มุมเฟสของสัญญาณ (วัดเป็นเรเดียน)

แนวโน้มของสัญญาณนี้คือการเกิดซ้ำหลังจากช่วงเวลาหนึ่งดังนั้นจึงเรียกว่าสัญญาณเป็นระยะ ช่วงเวลาของสัญญาณกำหนดเป็น;

$$T = \frac{2\pi }{\omega }$$

มุมมองแผนภาพของสัญญาณไซน์แสดงไว้ด้านล่าง

ฟังก์ชันสี่เหลี่ยม

สัญญาณจะบอกว่าเป็นประเภทฟังก์ชันสี่เหลี่ยมหากเป็นไปตามเงื่อนไขต่อไปนี้ -

$$\pi(\frac{t}{\tau}) = \begin{cases}1, & for\quad t\leq \frac{\tau}{2}\\0, & Otherwise\end{cases}$$

ด้วยความสมมาตรเกี่ยวกับแกน Y สัญญาณนี้จึงเรียกว่าสัญญาณคู่

สัญญาณพัลส์สามเหลี่ยม

สัญญาณใด ๆ ที่เป็นไปตามเงื่อนไขต่อไปนี้เรียกว่าสัญญาณสามเหลี่ยม

$$\Delta(\frac{t}{\tau}) = \begin{cases}1-(\frac{2|t|}{\tau}) & for|t|<\frac{\tau}{2}\\0 & for|t|>\frac{\tau}{2}\end{cases}$$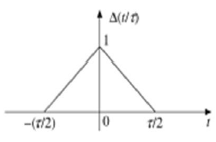

สัญญาณนี้สมมาตรเกี่ยวกับแกน Y ดังนั้นจึงเรียกได้ว่าเป็นสัญญาณคู่

เราได้เห็นว่าสัญญาณพื้นฐานสามารถแสดงในโดเมนเวลาต่อเนื่องได้อย่างไร ให้เราดูว่าสัญญาณพื้นฐานสามารถแสดงใน Discrete Time Domain ได้อย่างไร

ลำดับอิมพัลส์หน่วย

แสดงเป็นδ (n) ในโดเมนเวลาไม่ต่อเนื่องและสามารถกำหนดเป็น;

$$\delta(n)=\begin{cases}1, & for \quad n=0\\0, & Otherwise\end{cases}$$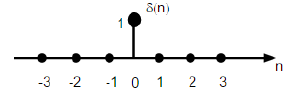

สัญญาณขั้นตอนของหน่วย

สัญญาณขั้นตอนหน่วยเวลาไม่ต่อเนื่องถูกกำหนดให้เป็น;

$$U(n)=\begin{cases}1, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$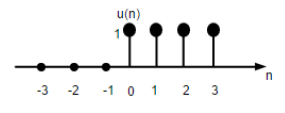

รูปด้านบนแสดงการแสดงกราฟิกของฟังก์ชันขั้นตอนที่ไม่ต่อเนื่อง

ฟังก์ชัน Unit Ramp

ฟังก์ชันทางลาดหน่วยแยกสามารถกำหนดเป็น -

$$r(n)=\begin{cases}n, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$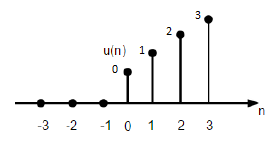

รูปที่ระบุด้านบนแสดงการแสดงกราฟิกของสัญญาณทางลาดที่ไม่ต่อเนื่อง

ฟังก์ชันพาราโบลา

ฟังก์ชันพาราโบลาของหน่วยไม่ต่อเนื่องแสดงเป็น p (n) และสามารถกำหนดเป็น;

$$p(n) = \begin{cases}\frac{n^{2}}{2} ,& for \quad n\geq0\\0, & for \quad n<0\end{cases}$$

ในแง่ของฟังก์ชันขั้นตอนหน่วยสามารถเขียนเป็น;

$$P(n) = \frac{n^{2}}{2}U(n)$$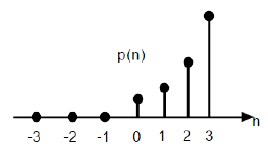

รูปที่ให้ไว้ด้านบนแสดงการแสดงกราฟิกของลำดับพาราโบลา

สัญญาณไซน์

สัญญาณเวลาต่อเนื่องทั้งหมดเป็นระยะ ลำดับไซน์ไทม์ที่ไม่ต่อเนื่องอาจเป็นระยะหรือไม่ก็ได้ ขึ้นอยู่กับค่าของω เพื่อให้สัญญาณเวลาไม่ต่อเนื่องเป็นคาบความถี่เชิงมุมωต้องเป็นผลคูณที่มีเหตุผลของ2π

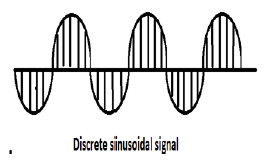
สัญญาณไซน์ที่ไม่ต่อเนื่องแสดงในรูปด้านบน

รูปแบบที่ไม่ต่อเนื่องของสัญญาณไซน์สามารถแสดงในรูปแบบ -

$$x(n) = A\sin(\omega n + \phi)$$

ที่นี่ A, ωและφมีความหมายตามปกติและ n คือจำนวนเต็ม ช่วงเวลาของสัญญาณไซน์ไม่ต่อเนื่องกำหนดโดย -

$$N =\frac{2\pi m}{\omega}$$

โดยที่ N และ m เป็นจำนวนเต็ม

สัญญาณเวลาต่อเนื่องสามารถจำแนกได้ตามเงื่อนไขหรือการดำเนินการที่แตกต่างกันของสัญญาณ

สัญญาณคู่และคี่

แม้แต่สัญญาณ

สัญญาณบอกว่าเป็นไปตามเงื่อนไขต่อไปนี้

$$x(-t) = x(t)$$

การย้อนเวลาของสัญญาณไม่ได้หมายความถึงการเปลี่ยนแปลงใด ๆ ของแอมพลิจูดที่นี่ ตัวอย่างเช่นพิจารณาคลื่นสามเหลี่ยมที่แสดงด้านล่าง

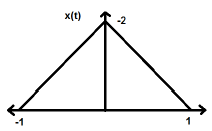
สัญญาณสามเหลี่ยมคือสัญญาณคู่ เนื่องจากมันสมมาตรเกี่ยวกับแกน Y เราสามารถพูดได้ว่าเป็นภาพสะท้อนเกี่ยวกับแกน Y

พิจารณาสัญญาณอื่นดังแสดงในรูปด้านล่าง

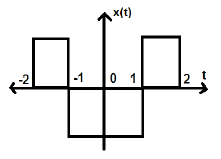
เราจะเห็นว่าสัญญาณข้างบนนั้นมีความสมมาตรเกี่ยวกับแกน Y

สัญญาณแปลก

สัญญาณจะบอกว่าเป็นเลขคี่หากเป็นไปตามเงื่อนไขต่อไปนี้

$$x(-t) = -x(t)$$

ที่นี่ทั้งการย้อนเวลาและการเปลี่ยนแปลงแอมพลิจูดจะเกิดขึ้นพร้อมกัน

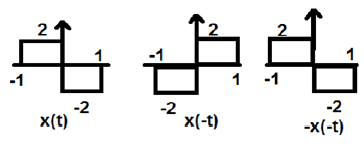
ในรูปด้านบนเราจะเห็นสัญญาณขั้นตอน x (t) ในการทดสอบว่าเป็นสัญญาณคี่หรือไม่อันดับแรกเราทำการย้อนเวลาเช่น x (-t) และผลลัพธ์จะเป็นดังที่แสดงในรูป จากนั้นเรากลับแอมพลิจูดของสัญญาณผลลัพธ์คือ –x (-t) และเราจะได้ผลลัพธ์ดังแสดงในรูป

ถ้าเราเปรียบเทียบรูปคลื่นแรกและรูปที่สามเราจะเห็นว่ามันเหมือนกันนั่นคือ x (t) = -x (-t) ซึ่งตรงตามเกณฑ์ของเรา ดังนั้นสัญญาณข้างต้นจึงเป็นสัญญาณคี่

ผลลัพธ์ที่สำคัญบางประการที่เกี่ยวข้องกับสัญญาณคู่และคี่มีให้ด้านล่าง

Even × Even = คู่
คี่×คี่ = คู่
Even × Odd = คี่
Even ± Even = Even
คี่±คี่ = คี่
Even ± Odd = ทั้งคู่หรือคี่

การแสดงสัญญาณใด ๆ ในรูปแบบคู่หรือคี่

สัญญาณบางอย่างไม่สามารถจำแนกเป็นประเภทคู่หรือคี่ได้โดยตรง สิ่งเหล่านี้แสดงเป็นการรวมกันของทั้งสัญญาณคู่และคี่

$$x(t)\rightarrow x_{e}(t)+x_{0}(t)$$

โดยที่ x _e (t) แทนสัญญาณคู่และ x _o (t) แทนสัญญาณคี่

$$x_{e}(t)=\frac{[x(t)+x(-t)]}{2}$$

และ

$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$

ตัวอย่าง

ค้นหาส่วนคู่และคี่ของสัญญาณ $x(n) = t+t^{2}+t^{3}$

Solution - จากการย้อนกลับ x (n) เราจะได้

$$x(-n) = -t+t^{2}-t^{3}$$

ตอนนี้ตามสูตรส่วนคู่

$$x_{e}(t) = \frac{x(t)+x(-t)}{2}$$

$$= \frac{[(t+t^{2}+t^{3})+(-t+t^{2}-t^{3})]}{2}$$

$$= t^{2}$$

ในทำนองเดียวกันตามสูตรส่วนที่แปลกคือ

$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$

$$= \frac{[(t+t^{2}+t^{3})-(-t+t^{2}-t^{3})]}{2}$$

$$= t+t^{3}$$

สัญญาณเป็นระยะและไม่เป็นระยะ

สัญญาณเป็นระยะ

สัญญาณเป็นระยะจะทำซ้ำตัวเองหลังจากช่วงเวลาหนึ่ง เราสามารถแสดงสิ่งนี้ในรูปสมการเป็น -

$$x(t) = x(t)\pm nT$$

โดยที่ n = จำนวนเต็ม (1,2,3 ……)

T = ช่วงเวลาพื้นฐาน (FTP) ≠ 0 และ≠∞

ช่วงเวลาพื้นฐาน (FTP) เป็นค่าบวกและค่าคงที่ที่เล็กที่สุดของเวลาที่สัญญาณเป็นระยะ

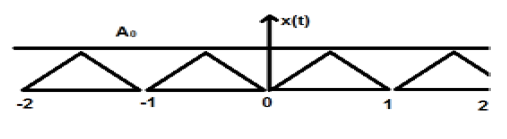
สัญญาณสามเหลี่ยมแสดงในรูปด้านบนของแอมพลิจูด A ที่นี่สัญญาณจะเกิดซ้ำทุก 1 วินาที ดังนั้นเราสามารถพูดได้ว่าสัญญาณเป็นระยะและ FTP คือ 1 วินาที

สัญญาณที่ไม่เป็นระยะ

เราสามารถพูดได้ง่ายๆว่าสัญญาณที่ไม่เป็นระยะนั้นไม่มีลักษณะเป็นช่วง ๆ เห็นได้ชัดว่าสัญญาณเหล่านี้จะไม่เกิดซ้ำหลังจากช่วงเวลาใด ๆ

สัญญาณที่ไม่เป็นระยะไม่เป็นไปตามรูปแบบที่แน่นอน ดังนั้นจึงไม่มีสมการทางคณิตศาสตร์ที่เฉพาะเจาะจงสามารถอธิบายได้

สัญญาณพลังงานและพลังงาน

สัญญาณกล่าวว่าเป็นสัญญาณพลังงานหากและเฉพาะในกรณีที่พลังงานทั้งหมดที่มีอยู่นั้น จำกัด และไม่ใช่ศูนย์ (0 <E <∞) ดังนั้นสำหรับสัญญาณประเภทพลังงานใด ๆ สัญญาณปกติทั้งหมดจะ จำกัด และไม่เป็นศูนย์

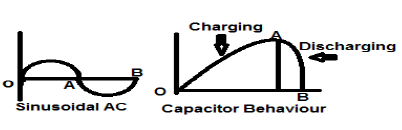
สัญญาณกระแสไฟฟ้ากระแสสลับไซน์เป็นตัวอย่างที่สมบูรณ์แบบของสัญญาณประเภทพลังงานเนื่องจากอยู่ในครึ่งรอบที่เป็นบวกในกรณีหนึ่งจากนั้นเป็นค่าลบในครึ่งรอบถัดไป ดังนั้นกำลังเฉลี่ยจึงกลายเป็นศูนย์

ตัวเก็บประจุแบบไม่สูญเสียเป็นตัวอย่างที่สมบูรณ์แบบของสัญญาณประเภทพลังงานเนื่องจากเมื่อเชื่อมต่อกับแหล่งที่มามันจะชาร์จได้ถึงระดับที่เหมาะสมและเมื่อถอดแหล่งที่มาตัวเก็บประจุจะกระจายพลังงานจำนวนเท่ากันผ่านโหลดและทำให้พลังงานเฉลี่ย ศูนย์.

สำหรับสัญญาณ จำกัด ใด ๆ x (t) พลังงานสามารถเป็นสัญลักษณ์เป็น E และเขียนเป็น;

$$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$

ความหนาแน่นสเปกตรัมของสัญญาณประเภทพลังงานให้ปริมาณพลังงานที่กระจายในระดับความถี่ต่างๆ

สัญญาณประเภทพลังงาน

สัญญาณกล่าวว่าเป็นสัญญาณประเภทพลังงานถ้าและเฉพาะในกรณีที่กำลังเฉลี่ยปกติจะ จำกัด และไม่ใช่ศูนย์เช่น (0 <p <∞) สำหรับสัญญาณประเภทพลังงานกำลังเฉลี่ยปกติจะ จำกัด และไม่เป็นศูนย์ สัญญาณประจำงวดเกือบทั้งหมดเป็นสัญญาณกำลังและกำลังเฉลี่ยของพวกเขานั้น จำกัด และไม่เป็นศูนย์

ในรูปแบบทางคณิตศาสตร์กำลังของสัญญาณ x (t) สามารถเขียนเป็น;

$$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$

ความแตกต่างระหว่างสัญญาณพลังงานและพลังงาน

ตารางต่อไปนี้สรุปความแตกต่างของสัญญาณพลังงานและพลังงาน

สัญญาณไฟ	สัญญาณพลังงาน
สัญญาณระยะปฏิบัติเป็นสัญญาณกำลัง	สัญญาณที่ไม่เป็นระยะคือสัญญาณพลังงาน
ที่นี่กำลังเฉลี่ยปกตินั้น จำกัด และไม่เป็นศูนย์	ที่นี่พลังงานที่ปรับให้เป็นมาตรฐานทั้งหมดมีค่า จำกัด และไม่เป็นศูนย์
ในทางคณิตศาสตร์ $$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$	ในทางคณิตศาสตร์ $$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$
การมีอยู่ของสัญญาณเหล่านี้ไม่มีที่สิ้นสุดเมื่อเวลาผ่านไป	สัญญาณเหล่านี้มีอยู่ในช่วงเวลา จำกัด
พลังงานของสัญญาณกำลังไม่มีที่สิ้นสุดในช่วงเวลาที่ไม่มีที่สิ้นสุด	พลังของสัญญาณพลังงานเป็นศูนย์ในช่วงเวลาที่ไม่มีที่สิ้นสุด

ตัวอย่างที่แก้ไข

Example 1 - ค้นหาพลังของสัญญาณ $z(t) = 2\cos(3\Pi t+30^{o})+4\sin(3\Pi +30^{o})$

Solution- สัญญาณทั้งสองข้างต้นมีมุมฉากซึ่งกันและกันเนื่องจากคำศัพท์ความถี่เหมือนกันและมีความแตกต่างเฟสเดียวกัน ดังนั้นพลังทั้งหมดจะเป็นการรวมพลังของแต่ละบุคคล

ปล่อย $z(t) = x(t)+y(t)$

ที่ไหน $x(t) = 2\cos (3\Pi t+30^{o})$ และ $y(t) = 4\sin(3\Pi +30^{o})$

พลังของ $x(t) = \frac{2^{2}}{2} = 2$

พลังของ $y(t) = \frac{4^{2}}{2} = 8$

ดังนั้น, $P(z) = p(x)+p(y) = 2+8 = 10$…ตอบ

Example 2 - ทดสอบว่าได้รับสัญญาณหรือไม่ $x(t) = t^{2}+j\sin t$ คอนจูเกตหรือไม่?

Solution- ตรงนี้ส่วนที่แท้จริงของ t ²คือส่วนที่เป็นคู่และส่วนที่แปลก (ในจินตนาการ)$\sin t$เป็นเรื่องแปลก ดังนั้นสัญญาณข้างต้นจึงเป็นสัญญาณ Conjugate

Example 3 - ตรวจสอบว่า $X(t)= \sin \omega t$ เป็นสัญญาณคี่หรือสัญญาณคู่

Solution - ให้ $X(t) = \sin \omega t$

โดยการย้อนเวลาเราจะได้ $\sin (-\omega t)$

แต่เรารู้ดีว่า $\sin(-\phi) = -\sin \phi$.

ดังนั้น,

$$\sin (-\omega t) = -\sin \omega t$$

นี่เป็นเงื่อนไขที่ทำให้สัญญาณเป็นคี่ ดังนั้น,$\sin \omega t$ เป็นสัญญาณคี่

เช่นเดียวกับสัญญาณเวลาแบบต่อเนื่องสัญญาณเวลาแบบไม่ต่อเนื่องสามารถจำแนกได้ตามเงื่อนไขหรือการดำเนินการของสัญญาณ

สัญญาณคู่และคี่

แม้แต่สัญญาณ

สัญญาณจะบอกว่าสม่ำเสมอหรือสมมาตรหากเป็นไปตามเงื่อนไขต่อไปนี้

$$x(-n) = x(n)$$

ที่นี่เราจะเห็นว่า x (-1) = x (1), x (-2) = x (2) และ x (-n) = x (n) ดังนั้นจึงเป็นสัญญาณคู่

สัญญาณแปลก

สัญญาณจะบอกว่าเป็นเลขคี่หากเป็นไปตามเงื่อนไขต่อไปนี้

$$x(-n) = -x(n)$$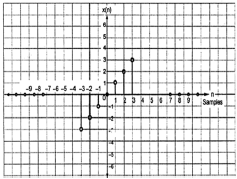

จากรูปจะเห็นว่า x (1) = -x (-1), x (2) = -x (2) และ x (n) = -x (-n) ดังนั้นจึงเป็นสัญญาณที่แปลกและต่อต้านสมมาตร

สัญญาณเป็นระยะและไม่เป็นระยะ

สัญญาณบอกเวลาที่ไม่ต่อเนื่องเป็นช่วง ๆ หากเป็นไปตามเงื่อนไขต่อไปนี้ -

$$x(n+N) = x(n)$$

ที่นี่สัญญาณ x (n) ซ้ำตัวเองหลังจากช่วงเวลา N สิ่งนี้สามารถเข้าใจได้ดีที่สุดโดยพิจารณาจากสัญญาณโคไซน์ -

$$x(n) = A \cos(2\pi f_{0}n+\theta)$$ $$x(n+N) = A\cos(2\pi f_{0}(n+N)+\theta) = A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$ $$= A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$

เพื่อให้สัญญาณเป็นระยะควรปฏิบัติตามเงื่อนไขต่อไปนี้

$$x(n+N) = x(n)$$ $$\Rightarrow A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta) = A \cos(2\pi f_{0}n+\theta)$$

กล่าวคือ $2\pi f_{0}N$ เป็นผลคูณเชิงปริพันธ์ของ $2\pi$

$$2\pi f_{0}N = 2\pi K$$ $$\Rightarrow N = \frac{K}{f_{0}}$$

ความถี่ของสัญญาณไซน์ที่ไม่ต่อเนื่องถูกคั่นด้วยอินทิกรัลพหุคูณของ $2\pi$.

สัญญาณพลังงานและพลังงาน

สัญญาณพลังงาน

พลังงานของสัญญาณเวลาไม่ต่อเนื่องแสดงเป็น E ในทางคณิตศาสตร์สามารถเขียนเป็น;

$$E = \displaystyle \sum\limits_{n=-\infty}^{+\infty}|x(n)|^2$$

หากแต่ละค่าของ $x(n)$กำลังสองและเพิ่มเราได้รับสัญญาณพลังงาน ที่นี่$x(n)$ คือสัญญาณพลังงานและพลังงานของมันมี จำกัด เมื่อเวลาผ่านไปคือ $ 0 <E <\ infty $

สัญญาณไฟ

กำลังเฉลี่ยของสัญญาณที่ไม่ต่อเนื่องแสดงเป็น P. ในทางคณิตศาสตร์ซึ่งสามารถเขียนเป็น;

$$P = \lim_{N \to \infty} \frac{1}{2N+1}\displaystyle\sum\limits_{n=-N}^{+N} |x(n)|^2$$

ที่นี่อำนาจ จำกัด คือ 0 <P <∞ อย่างไรก็ตามมีสัญญาณบางอย่างที่ไม่ใช่สัญญาณประเภทพลังงานหรือพลังงาน

มีสัญญาณอื่น ๆ ซึ่งเป็นผลมาจากการดำเนินการกับพวกเขา สัญญาณทั่วไปบางประเภทจะกล่าวถึงด้านล่าง

สัญญาณผัน

สัญญาณซึ่งเป็นไปตามเงื่อนไข $x(t) = x*(-t)$ เรียกว่าสัญญาณคอนจูเกต

ปล่อย $x(t) = a(t)+jb(t)$... eqn. 1

ดังนั้น, $x(-t) = a(-t)+jb(-t)$

และ $x*(-t) = a(-t)-jb(-t)$... eqn. 2

ตามเงื่อนไข $x(t) = x*(-t)$

หากเราเปรียบเทียบทั้งสมการที่ได้มา 1 และ 2 เราจะเห็นว่าส่วนจริงเป็นเลขคู่ในขณะที่ส่วนจินตภาพเป็นเลขคี่ นี่คือเงื่อนไขสำหรับสัญญาณที่จะเป็นประเภทคอนจูเกต

Conjugate Anti-Symmetric Signals

สัญญาณซึ่งเป็นไปตามเงื่อนไข $x(t) = -x*(-t)$ เรียกว่าสัญญาณต่อต้านสมมาตรคอนจูเกต

ปล่อย $x(t) = a(t)+jb(t)$... eqn. 1

ดังนั้น $x(-t) = a(-t)+jb(-t)$

และ $x*(-t) = a(-t)-jb(-t)$

$-x*(-t) = -a(-t)+jb(-t)$... eqn. 2

ตามเงื่อนไข $x(t) = -x*(-t)$

ทีนี้ลองเปรียบเทียบอีกครั้งทั้งสมการเหมือนกับที่เราทำกับสัญญาณคอนจูเกต ที่นี่เราจะพบว่าส่วนจริงเป็นเลขคี่และส่วนจินตภาพเป็นเลขคู่ นี่เป็นเงื่อนไขสำหรับสัญญาณที่จะกลายเป็นประเภทต่อต้านสมมาตรที่ผันแปร

ตัวอย่าง

ให้สัญญาณที่กำหนด $x(t) = \sin t+jt^{2}$.

นี่คือส่วนที่แท้จริง $\sin t$ เป็นเรื่องแปลกและเป็นส่วนในจินตนาการ $t^2$เป็นคู่ ดังนั้นสัญญาณนี้จึงสามารถจัดเป็นสัญญาณต่อต้านสมมาตรแบบคอนจูเกต

ฟังก์ชันใด ๆ สามารถแบ่งออกเป็นสองส่วน ส่วนหนึ่งเป็นสมมาตรคอนจูเกตและส่วนอื่น ๆ ที่เป็นคอนจูเกตต่อต้านสมมาตร ดังนั้นสัญญาณ x (t) ใด ๆ จึงสามารถเขียนเป็น

$$x(t) = xcs(t)+xcas(t)$$

ที่ไหน $xcs(t)$ คือผันสัญญาณสมมาตรและ $xcas(t)$ คือการผันสัญญาณต่อต้านสมมาตร

$$xcs(t) = \frac{[x(t)+x*(-t)]}{2}$$

และ

$$xcas(t) = \frac{[x(t)-x*(-t)]}{2}$$

สัญญาณสมมาตรครึ่งคลื่น

เมื่อสัญญาณตรงตามเงื่อนไข $cx(t) = -x(t\pm (\frac{T_{0}}{2}))$เรียกว่าสัญญาณสมมาตรครึ่งคลื่น ที่นี่การย้อนกลับแอมพลิจูดและการเปลี่ยนเวลาของสัญญาณจะเกิดขึ้นครึ่งเวลา สำหรับสัญญาณสมมาตรครึ่งคลื่นค่าเฉลี่ยจะเป็นศูนย์ แต่ไม่ใช่กรณีนี้เมื่อสถานการณ์กลับกัน

พิจารณาสัญญาณ x (t) ดังแสดงในรูป A ด้านบน ขั้นตอนแรกคือการเปลี่ยนเวลาของสัญญาณและทำให้มัน$x[t-(\frac{T}{2})]$. ดังนั้นสัญญาณใหม่จึงเปลี่ยนไปดังแสดงในรูป B ถัดไปเรากลับแอมพลิจูดของสัญญาณนั่นคือทำให้มัน$-x[t-(\frac{T}{2})]$ ดังแสดงในรูป C. เนื่องจากสัญญาณนี้จะเกิดขึ้นซ้ำ ๆ หลังจากการขยับครึ่งเวลาและการกลับแอมพลิจูดซึ่งเป็นสัญญาณสมมาตรครึ่งคลื่น

สัญญาณมุมฉาก

สัญญาณสองตัว x (t) และ y (t) ถูกกล่าวว่าตั้งฉากกันหากเป็นไปตามเงื่อนไขสองข้อต่อไปนี้

Condition 1 - $\int_{-\infty}^{\infty}x(t)y(t) = 0$ [สำหรับสัญญาณที่ไม่เป็นระยะ]

Condition 2 - $\int x(t)y(t) = 0$ [สำหรับสัญญาณเป็นระยะ]

สัญญาณซึ่งมีฮาร์มอนิกแปลก ๆ (3 ^rd , 5 ^th , 7 ^th ... ฯลฯ ) และมีความถี่ที่แตกต่างกันมีมุมฉากซึ่งกันและกัน

ในสัญญาณประเภทตรีโกณมิติฟังก์ชันไซน์และฟังก์ชันโคไซน์จะตั้งฉากกันด้วยเช่นกัน หากมีความถี่เท่ากันและอยู่ในเฟสเดียวกัน ในลักษณะเดียวกันสัญญาณ DC (สัญญาณกระแสตรง) และสัญญาณไซน์จะตั้งฉากกัน ถ้า x (t) และ y (t) เป็นสองสัญญาณที่ตั้งฉากกันและ$z(t) = x(t)+y(t)$ จากนั้นกำลังและพลังงานของ z (t) สามารถเขียนเป็น;

$$P(z) = p(x)+p(y)$$ $$E(z) = E(x)+E(y)$$

ตัวอย่าง

วิเคราะห์สัญญาณ: $z(t) = 3+4\sin(2\pi t+30^0)$

ในที่นี้สัญญาณประกอบด้วยสัญญาณ DC (3) และฟังก์ชันไซน์หนึ่งฟังก์ชัน ดังนั้นโดยคุณสมบัติสัญญาณนี้จึงเป็นสัญญาณมุมฉากและสัญญาณย่อยทั้งสองในนั้นมีมุมฉากซึ่งกันและกัน

การขยับหมายถึงการเคลื่อนที่ของสัญญาณทั้งในโดเมนเวลา (รอบแกน Y) หรือในโดเมนแอมพลิจูด (รอบแกน X) ดังนั้นเราสามารถแบ่งประเภทของการขยับออกเป็นสองประเภทที่เรียกว่าการเปลี่ยนเวลาและการขยับแอมพลิจูดซึ่งจะกล่าวถึงต่อไปด้านล่าง

การเปลี่ยนเวลา

การเปลี่ยนเวลาหมายถึงการเปลี่ยนสัญญาณในโดเมนเวลา ในทางคณิตศาสตร์สามารถเขียนเป็น

$$x(t) \rightarrow y(t+k)$$

ค่า K นี้อาจเป็นบวกหรืออาจเป็นลบ ตามสัญลักษณ์ของค่า k เรามีการขยับสองประเภทที่เรียกว่าการขยับขวาและการขยับซ้าย

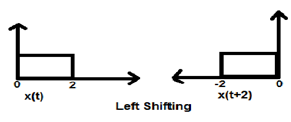
กรณีที่ 1 (K> 0)

เมื่อ K มากกว่าศูนย์การขยับของสัญญาณจะเกิดขึ้นไปทาง "ซ้าย" ในโดเมนเวลา ดังนั้นการเปลี่ยนประเภทนี้จึงเรียกว่าการขยับซ้ายของสัญญาณ

Example

กรณีที่ 2 (K <0)

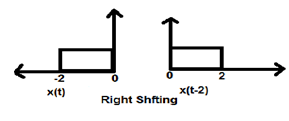
เมื่อ K น้อยกว่าศูนย์การเปลี่ยนสัญญาณจะเกิดขึ้นไปทางขวาในโดเมนเวลา ดังนั้นการเปลี่ยนประเภทนี้จึงเรียกว่าการขยับขวา

Example

รูปด้านล่างแสดงการเปลี่ยนสัญญาณอย่างถูกต้องโดย 2

การขยับแอมพลิจูด

การเปลี่ยนแอมพลิจูดหมายถึงการเปลี่ยนสัญญาณในโดเมนแอมพลิจูด (รอบแกน X) ในทางคณิตศาสตร์สามารถแสดงเป็น -

$$x(t) \rightarrow x(t)+K$$

ค่า K นี้อาจเป็นบวกหรือลบ ดังนั้นเราจึงมีการเปลี่ยนแอมพลิจูดสองประเภทซึ่งจะกล่าวถึงต่อไปด้านล่าง

กรณีที่ 1 (K> 0)

เมื่อ K มีค่ามากกว่าศูนย์การขยับของสัญญาณจะเกิดขึ้นในแกน x ดังนั้นการขยับประเภทนี้จึงเรียกว่าการขยับขึ้น

Example

ให้เราพิจารณาสัญญาณ x (t) ซึ่งได้รับเป็น;

$$x = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$

ให้เรานำ K = + 1 เพื่อให้สัญญาณใหม่สามารถเขียนเป็น -

$y(t) \rightarrow x(t)+1$ ดังนั้นในที่สุด y (t) สามารถเขียนเป็น;

$$x(t) = \begin{cases}1, & t < 0\\2, & 0\leq t\leq 2\\ 1, & t>0\end{cases}$$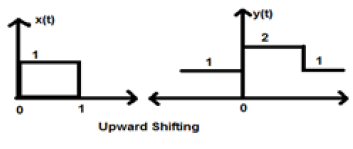

กรณีที่ 2 (K <0)

เมื่อ K น้อยกว่าศูนย์การขยับของสัญญาณจะเกิดขึ้นไปด้านล่างในแกน X- ดังนั้นจึงเรียกว่าการขยับลงของสัญญาณ

Example

ให้เราพิจารณาสัญญาณ x (t) ซึ่งได้รับเป็น;

$$x(t) = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$

ให้เรานำ K = -1 เพื่อให้สัญญาณใหม่สามารถเขียนเป็น;

$y(t)\rightarrow x(t)-1$ ดังนั้นในที่สุด y (t) สามารถเขียนเป็น;

$$y(t) = \begin{cases}-1, & t < 0\\0, & 0\leq t\leq 2\\ -1, & t>0\end{cases}$$

การสเกลของสัญญาณหมายถึงค่าคงที่จะคูณกับเวลาหรือแอมพลิจูดของสัญญาณ

การปรับเวลา

ถ้าค่าคงที่คูณกับแกนเวลาจะเรียกว่าการปรับเวลา สิ่งนี้สามารถแทนค่าทางคณิตศาสตร์เป็น;

$x(t) \rightarrow y(t) = x(\alpha t)$ หรือ $x(\frac{t}{\alpha})$; โดยที่α≠ 0

ดังนั้นแกน y เหมือนกันขนาดแกน x จะลดลงหรือเพิ่มขึ้นตามสัญลักษณ์ของค่าคงที่ (ไม่ว่าจะเป็นบวกหรือลบ) ดังนั้นการปรับขนาดจึงสามารถแบ่งออกเป็นสองประเภทตามที่กล่าวไว้ด้านล่าง

การบีบอัดเวลา

เมื่อใดก็ตามที่อัลฟามีค่ามากกว่าศูนย์แอมพลิจูดของสัญญาณจะถูกหารด้วยอัลฟาในขณะที่ค่าของแกน Y ยังคงเท่าเดิม ซึ่งเรียกว่าการบีบอัดเวลา

Example

ให้เราพิจารณาสัญญาณ x (t) ซึ่งแสดงดังรูปด้านล่าง ให้เราหาค่าของอัลฟ่าเป็น 2 ดังนั้น y (t) จะเป็น x (2t) ซึ่งแสดงในรูปที่กำหนด

เห็นได้ชัดจากตัวเลขด้านบนว่าขนาดเวลาในแกน y ยังคงเท่าเดิม แต่แอมพลิจูดในแกน x ลดลงจาก 4 เป็น 2 ดังนั้นจึงเป็นกรณีของการบีบอัดเวลา

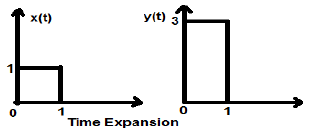
การขยายเวลา

เมื่อเวลาถูกหารด้วยอัลฟ่าคงที่ขนาดแกน Y ของสัญญาณจะได้รับคูณอัลฟาคูณโดยรักษาขนาดแกน X ตามที่เป็นอยู่ ดังนั้นจึงเรียกว่าสัญญาณประเภทการขยายเวลา

Example

ให้เราพิจารณาสัญญาณกำลังสอง x (t) ขนาด 1 เมื่อเราปรับขนาดมันด้วยค่าคงที่ 3 เช่นนั้น $x(t) \rightarrow y(t) \rightarrow x(\frac{t}{3})$จากนั้นแอมพลิจูดของสัญญาณจะถูกแก้ไข 3 ครั้งซึ่งแสดงในรูปด้านล่าง

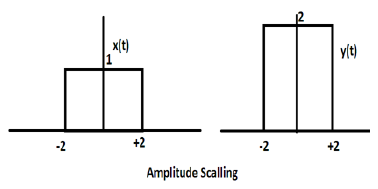
การปรับขนาดความกว้าง

การคูณค่าคงที่ด้วยแอมพลิจูดของสัญญาณทำให้เกิดการปรับขนาดแอมพลิจูด ขึ้นอยู่กับสัญลักษณ์ของค่าคงที่อาจเป็นได้ทั้งการปรับขนาดแอมพลิจูดหรือการลดทอน ให้เราพิจารณาสัญญาณคลื่นสี่เหลี่ยม x (t) = Π (t / 4)

สมมติว่าเรากำหนดฟังก์ชันอื่น y (t) = 2 Π (t / 4) ในกรณีนี้ค่าของแกน y จะเพิ่มเป็นสองเท่าโดยคงค่าแกนเวลาไว้ตามเดิม ดังแสดงในรูปด้านล่าง

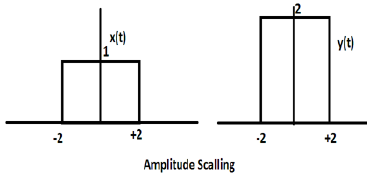
พิจารณาฟังก์ชันคลื่นสี่เหลี่ยมอื่นที่กำหนดเป็น z (t) โดยที่ z (t) = 0.5 Π (t / 4) ในที่นี้แอมพลิจูดของฟังก์ชัน z (t) จะเป็นครึ่งหนึ่งของ x (t) คือแกนเวลายังคงเท่าเดิมแกนแอมพลิจูดจะลดลงครึ่งหนึ่ง นี่คือภาพประกอบที่แสดงด้านล่าง

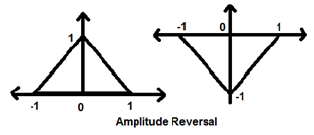
เมื่อใดก็ตามที่เวลาในสัญญาณคูณด้วย -1 สัญญาณจะกลับกัน สร้างภาพสะท้อนเกี่ยวกับแกน Y หรือ X สิ่งนี้เรียกว่าการกลับรายการของสัญญาณ

การกลับรายการสามารถแบ่งออกเป็นสองประเภทตามเงื่อนไขว่าเวลาหรือแอมพลิจูดของสัญญาณจะคูณด้วย -1

การย้อนเวลา

เมื่อใดก็ตามที่เวลาของสัญญาณคูณด้วย -1 จะเรียกว่าการย้อนเวลาของสัญญาณ ในกรณีนี้สัญญาณจะสร้างภาพสะท้อนเกี่ยวกับแกน Y ในทางคณิตศาสตร์สามารถเขียนเป็น;

$$x(t) \rightarrow y(t) \rightarrow x(-t)$$

สิ่งนี้สามารถเข้าใจได้ดีที่สุดจากตัวอย่างต่อไปนี้

จากตัวอย่างข้างต้นเราจะเห็นได้อย่างชัดเจนว่าสัญญาณกลับกันเกี่ยวกับแกน Y ดังนั้นจึงเป็นการปรับเวลาแบบหนึ่งเช่นกัน แต่ที่นี่ปริมาณมาตราส่วนคือ (-1) เสมอ

การกลับแอมพลิจูด

เมื่อใดก็ตามที่ความกว้างของสัญญาณคูณด้วย -1 จะเรียกว่าการกลับกันของแอมพลิจูด ในกรณีนี้สัญญาณจะสร้างภาพสะท้อนเกี่ยวกับแกน X ในทางคณิตศาสตร์สามารถเขียนเป็น;

$$x(t)\rightarrow y(t)\rightarrow -x(t)$$

ลองพิจารณาตัวอย่างต่อไปนี้ การกลับแอมพลิจูดสามารถมองเห็นได้ชัดเจน

การดำเนินการที่สำคัญสองอย่างที่ดำเนินการกับสัญญาณคือการสร้างความแตกต่างและการรวม

ความแตกต่าง

ความแตกต่างของสัญญาณใด ๆ x (t) หมายถึงการแสดงความชันของสัญญาณนั้นตามเวลา ในทางคณิตศาสตร์จะแสดงเป็น;

$$x(t)\rightarrow \frac{dx(t)}{dt}$$

ในกรณีของการสร้างความแตกต่างของ OPAMP วิธีการนี้มีประโยชน์มาก เราสามารถแยกความแตกต่างของสัญญาณในรูปแบบกราฟิกได้อย่างง่ายดายแทนที่จะใช้สูตร อย่างไรก็ตามเงื่อนไขคือสัญญาณต้องเป็นแบบสี่เหลี่ยมหรือสามเหลี่ยมซึ่งส่วนใหญ่จะเกิดขึ้น

สัญญาณดั้งเดิม	สัญญาณที่แตกต่าง
ทางลาด	ขั้นตอน
ขั้นตอน	แรงกระตุ้น
แรงกระตุ้น	1

ตารางด้านบนแสดงให้เห็นถึงสภาพของสัญญาณหลังจากที่มีความแตกต่าง ตัวอย่างเช่นสัญญาณทางลาดจะแปลงเป็นสัญญาณขั้นตอนหลังจากการแยกความแตกต่าง ในทำนองเดียวกันสัญญาณขั้นตอนของหน่วยจะกลายเป็นสัญญาณอิมพัลส์

ตัวอย่าง

ให้สัญญาณที่ให้กับเราเป็น $x(t) = 4[r(t)-r(t-2)]$. เมื่อมีการลงจุดสัญญาณนี้จะมีลักษณะเหมือนสัญญาณทางด้านซ้ายของรูปด้านล่าง ตอนนี้เป้าหมายของเราคือการแยกสัญญาณที่กำหนด

เริ่มต้นด้วยเราจะเริ่มแยกความแตกต่างของสมการที่กำหนด เรารู้ว่าสัญญาณทางลาดหลังจากการแยกความแตกต่างให้สัญญาณขั้นตอนของหน่วย

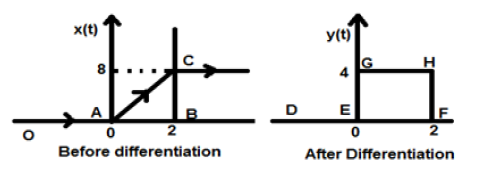
ดังนั้นสัญญาณผลลัพธ์ของเรา y (t) สามารถเขียนเป็น;

$y(t) = \frac{dx(t)}{dt}$

$= \frac{d4[r(t)-r(t-2)]}{dt}$

$= 4[u(t)-u(t-2)]$

ตอนนี้สัญญาณนี้ถูกพล็อตในที่สุดซึ่งแสดงไว้ที่ด้านขวามือของรูปด้านบน

การรวมสัญญาณใด ๆ หมายถึงการรวมของสัญญาณนั้นภายใต้โดเมนเวลาเฉพาะเพื่อให้ได้สัญญาณที่แก้ไข ในทางคณิตศาสตร์สามารถแสดงเป็น -

$$x(t)\rightarrow y(t) = \int_{-\infty}^{t}x(t)dt$$

นอกจากนี้ในกรณีส่วนใหญ่เราสามารถทำการรวมทางคณิตศาสตร์และค้นหาสัญญาณที่ได้ แต่การรวมโดยตรงแบบต่อเนื่องอย่างรวดเร็วเป็นไปได้สำหรับสัญญาณที่แสดงในรูปแบบกราฟิกสี่เหลี่ยม เช่นเดียวกับการสร้างความแตกต่างที่นี่เราจะอ้างอิงตารางเพื่อให้ได้ผลลัพธ์อย่างรวดเร็ว

สัญญาณดั้งเดิม	สัญญาณรวม
1	แรงกระตุ้น
แรงกระตุ้น	ขั้นตอน
ขั้นตอน	ทางลาด

ตัวอย่าง

ให้เราพิจารณาสัญญาณ $x(t) = u(t)-u(t-3)$. ดังแสดงในรูปที่ 1 ด้านล่าง ชัดเจนเราจะเห็นว่ามันเป็นสัญญาณขั้นตอน ตอนนี้เราจะรวมเข้าด้วยกัน จากตารางเราทราบว่าการรวมสัญญาณขั้นตอนทำให้เกิดสัญญาณทางลาด

อย่างไรก็ตามเราจะคำนวณทางคณิตศาสตร์

$y(t) = \int_{-\infty}^{t}x(t)dt$

$= \int_{-\infty}^{t}[u(t)-u(t-3)]dt$

$= \int_{-\infty}^{t}u(t)dt-\int_{-\infty}^{t}u(t-3)dt$

$= r(t)-r(t-3)$

พล็อตเช่นเดียวกันดังแสดงในรูปที่ 2

การแปลงสัญญาณสองสัญญาณในโดเมนเวลาเทียบเท่ากับการคูณของการแทนค่าในโดเมนความถี่ ในทางคณิตศาสตร์เราสามารถเขียนการแปลงสัญญาณสองสัญญาณเป็น

$$y(t) = x_{1}(t)*x_{2}(t)$$ $$= \int_{-\infty}^{\infty}x_{1}(p).x_{2}(t-p)dp$$

ขั้นตอนในการ Convolution

รับสัญญาณ x ₁ (t) และใส่ t = p ที่นั่นเพื่อให้เป็น x ₁ (p)
รับสัญญาณ x ₂ (t) และทำขั้นตอนที่ 1 และทำให้เป็น x ₂ (p)
ทำการพับสัญญาณคือ x ₂ (-p)
ทำการเปลี่ยนเวลาของสัญญาณข้างต้น x ₂ [- (pt)]
จากนั้นทำการคูณของสัญญาณทั้งสอง กล่าวคือ$x_{1}(p).x_{2}[−(p−t)]$

ตัวอย่าง

ให้เราทำการแปลงสัญญาณขั้นตอน u (t) ด้วยชนิดของมันเอง

$y(t) = u(t)*u(t)$

$= \int_{-\infty}^{\infty}[u(p).u[-(p-t)]dp$

ตอนนี้ t นี้สามารถมากกว่าหรือน้อยกว่าศูนย์ซึ่งแสดงในรูปด้านล่าง

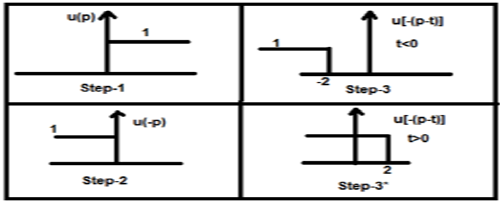
ดังนั้นจากกรณีข้างต้นผลลัพธ์จึงเกิดขึ้นตามความเป็นไปได้ดังต่อไปนี้

$y(t) = \begin{cases}0, & if\quad t<0\\\int_{0}^{t}1dt, & for\quad t>0\end{cases}$

$= \begin{cases}0, & if\quad t<0\\t, & t>0\end{cases} = r(t)$

คุณสมบัติของ Convolution

สับเปลี่ยน

มันระบุว่าลำดับการแปลงไม่สำคัญซึ่งสามารถแสดงทางคณิตศาสตร์เป็น

$$x_{1}(t)*x_{2}(t) = x_{2}(t)*x_{1}(t)$$

Associative

มันระบุว่าลำดับของการสนทนาที่เกี่ยวข้องกับสัญญาณสามอย่างอาจเป็นอะไรก็ได้ ในทางคณิตศาสตร์สามารถแสดงเป็น;

$$x_{1}(t)*[x_{2}(t)*x_{3}(t)] = [x_{1}(t)*x_{2}(t)]*x_{3}(t)$$

แจกจ่าย

สามารถเพิ่มสัญญาณสองสัญญาณก่อนจากนั้นจึงสามารถแปลงสัญญาณเป็นสัญญาณที่สามได้ สิ่งนี้เทียบเท่ากับการแปลงสัญญาณสองสัญญาณทีละสัญญาณกับสัญญาณที่สามและเพิ่มในที่สุด ในทางคณิตศาสตร์สามารถเขียนเป็น;

$$x_{1}(t)*[x_{2}(t)+x_{3}(t)] = [x_{1}(t)*x_{2}(t)+x_{1}(t)*x_{3}(t)]$$

พื้นที่

หากสัญญาณเป็นผลมาจากการแปลงสัญญาณสองสัญญาณพื้นที่ของสัญญาณจะเป็นการคูณของสัญญาณแต่ละตัว ในทางคณิตศาสตร์สามารถเขียนได้

ถ้า $y(t) = x_{1}*x_{2}(t)$

จากนั้นพื้นที่ของ y (t) = พื้นที่ของ x ₁ (t) X พื้นที่ของ x ₂ (t)

การปรับขนาด

หากสัญญาณสองสัญญาณถูกปรับขนาดเป็นค่าคงที่ที่ไม่รู้จัก“ a” และการ Convolution เสร็จสิ้นสัญญาณผลลัพธ์จะถูกแปลงเป็นค่าคงที่“ a” เดียวกันและจะถูกหารด้วยปริมาณดังที่แสดงด้านล่าง

ถ้า, $x_{1}(t)*x_{2}(t) = y(t)$

จากนั้น $x_{1}(at)*x_{2}(at) = \frac{y(at)}{a}, a \ne 0$

ล่าช้า

สมมติว่าสัญญาณ y (t) เป็นผลมาจากการแปลงสัญญาณสองสัญญาณ x1 (t) และ x2 (t) หากสัญญาณทั้งสองล่าช้าตามเวลา t1 และ t2 ตามลำดับสัญญาณผลลัพธ์ y (t) จะล่าช้าโดย (t1 + t2) ในทางคณิตศาสตร์สามารถเขียนเป็น -

ถ้า, $x_{1}(t)*x_{2}(t) = y(t)$

จากนั้น $x_{1}(t-t_{1})*x_{2}(t-t_{2}) = y[t-(t_{1}+t_{2})]$

ตัวอย่างที่แก้ไข

Example 1 - ค้นหาการแปลงสัญญาณ u (t-1) และ u (t-2)

Solution- สัญญาณที่ให้คือ u (t-1) และ u (t-2) การสนทนาของพวกเขาสามารถทำได้ดังที่แสดงด้านล่าง -

$y(t) = u(t-1)*u(t-2)$

$y(t) = \int_{-\infty}^{+\infty}[u(t-1).u(t-2)]dt$

$= r(t-1)+r(t-2)$

$= r(t-3)$

Example 2 - ค้นหาการแปลงสัญญาณสองสัญญาณที่กำหนดโดย

$x_{1}(n) = \lbrace 3,-2, 2\rbrace $

$x_{2}(n) = \begin{cases}2, & 0\leq n\leq 4\\0, & x > elsewhere\end{cases}$

Solution -

x ₂ (n) สามารถถอดรหัสเป็น$x_{2}(n) = \lbrace 2,2,2,2,2\rbrace Originalfirst$

ให้ x ₁ (n) ก่อนหน้านี้$= \lbrace 3,-2,3\rbrace = 3-2Z^{-1}+2Z^{-2}$

ในทำนองเดียวกัน $x_{2}(z) = 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$

สัญญาณผลลัพธ์

$X(Z) = X_{1}(Z)X_{2}(z)$

$= \lbrace 3-2Z^{-1}+2Z^{-2}\rbrace \times \lbrace 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}\rbrace$

$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+6Z^{-4}+6Z^{-5}$

การแปลง Z แบบผกผันข้างต้นเราจะได้รับสัญญาณผลลัพธ์เป็น

$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$ ต้นกำเนิดที่หนึ่ง

Example 3 - กำหนด Convolution ของ 2 สัญญาณต่อไปนี้ -

$x(n) = \lbrace 2,1,0,1\rbrace$

$h(n) = \lbrace 1,2,3,1\rbrace$

Solution -

เราได้รับการแปลงสัญญาณ Z

$x(z) = 2+2Z^{-1}+2Z^{-3}$

และ $h(n) = 1+2Z^{-1}+3Z^{-2}+Z^{-3}$

ตอนนี้การแปลงสัญญาณสองสัญญาณหมายถึงการคูณการแปลง Z ของพวกเขา

นั่นคือ $Y(Z) = X(Z) \times h(Z)$

$= \lbrace 2+2Z^{-1}+2Z^{-3}\rbrace \times \lbrace 1+2Z^{-1}+3Z^{-2}+Z^{-3}\rbrace$

$= \lbrace 2+5Z^{-1}+8Z^{-2}+6Z^{-3}+3Z^{-4}+3Z^{-5}+Z^{-6}\rbrace$

การแปลง Z แบบผกผันสัญญาณผลลัพธ์สามารถเขียนเป็น;

$y(n) = \lbrace 2,5,8,6,6,1 \rbrace Originalfirst$

บางระบบมีข้อเสนอแนะและบางระบบไม่มี สิ่งเหล่านี้ซึ่งไม่มีระบบป้อนกลับผลลัพธ์จะขึ้นอยู่กับค่าปัจจุบันของอินพุตเท่านั้น ไม่มีมูลค่าในอดีตของข้อมูลในขณะนั้น ระบบประเภทนี้เรียกว่าระบบคงที่ มันไม่ได้ขึ้นอยู่กับมูลค่าในอนาคตด้วย

เนื่องจากระบบเหล่านี้ไม่มีการบันทึกในอดีตดังนั้นจึงไม่มีหน่วยความจำใด ๆ ดังนั้นเราจึงกล่าวว่าระบบคงที่ทั้งหมดเป็นระบบที่ไม่มีหน่วยความจำ ให้เราเป็นตัวอย่างเพื่อทำความเข้าใจแนวคิดนี้ให้ดียิ่งขึ้น

ตัวอย่าง

ให้เราตรวจสอบว่าระบบต่อไปนี้เป็นระบบคงที่หรือไม่

$y(t) = x(t)+x(t-1)$
$y(t) = x(2t)$
$y(t) = x = \sin [x(t)]$

ก) $y(t) = x(t)+x(t-1)$

ในที่นี้ x (t) คือมูลค่าปัจจุบัน ไม่มีความสัมพันธ์กับค่าที่ผ่านมาของเวลา ดังนั้นจึงเป็นระบบคงที่ อย่างไรก็ตามในกรณีของ x (t-1) ถ้าเราใส่ t = 0 มันจะลดเป็น x (-1) ซึ่งขึ้นอยู่กับค่าที่ผ่านมา ดังนั้นจึงไม่คงที่ ดังนั้นที่นี่ y (t) ไม่ใช่ระบบคงที่

ข) $y(t) = x(2t)$

ถ้าเราแทนที่ t = 2 ผลลัพธ์จะเป็น y (t) = x (4) อีกครั้งขึ้นอยู่กับมูลค่าในอนาคต ดังนั้นจึงไม่ใช่ระบบคงที่

ค) $y(t) = x = \sin [x(t)]$

ในนิพจน์นี้เรากำลังจัดการกับฟังก์ชันไซน์ ช่วงของฟังก์ชันไซน์อยู่ระหว่าง -1 ถึง +1 ดังนั้นค่าใดก็ตามที่เราแทนที่ด้วย x (t) เราจะได้ระหว่าง -1 ถึง +1 ดังนั้นเราสามารถพูดได้ว่ามันไม่ได้ขึ้นอยู่กับคุณค่าในอดีตหรืออนาคตใด ๆ ดังนั้นจึงเป็นระบบคงที่

จากตัวอย่างข้างต้นเราสามารถสรุปได้ดังนี้ -

ระบบใด ๆ ที่มีการเปลี่ยนเวลาไม่คงที่
ระบบใด ๆ ที่มีการเปลี่ยนแอมพลิจูดก็ไม่คงที่เช่นกัน
กรณีการรวมและการสร้างความแตกต่างก็ไม่คงที่เช่นกัน

หากระบบขึ้นอยู่กับค่าในอดีตและอนาคตของสัญญาณในช่วงเวลาใดเวลาหนึ่งระบบจะเรียกว่าระบบไดนามิก ซึ่งแตกต่างจากระบบคงที่สิ่งเหล่านี้ไม่ใช่ระบบที่มีหน่วยความจำน้อยกว่า พวกเขาเก็บค่าในอดีตและอนาคต ดังนั้นพวกเขาต้องการหน่วยความจำบางอย่าง ให้เราเข้าใจทฤษฎีนี้ดีขึ้นผ่านตัวอย่างบางส่วน

ตัวอย่าง

ค้นหาว่าระบบต่อไปนี้เป็นแบบไดนามิกหรือไม่

a) $y(t) = x(t+1)$

ในกรณีนี้ถ้าเราใส่ t = 1 ในสมการมันจะถูกแปลงเป็น x (2) ซึ่งเป็นค่าตามอนาคต เนื่องจากที่นี่เราให้อินพุตเป็น 1 แต่กำลังแสดงค่าสำหรับ x (2) เนื่องจากเป็นสัญญาณที่ต้องพึ่งพาในอนาคตจึงเห็นได้ชัดว่าเป็นระบบไดนามิก

b) $y(t) = Real[x(t)]$

$$= \frac{[x(t)+x(t)^*]}{2}$$

ในกรณีนี้ค่าใดก็ตามที่เราใส่ไว้จะแสดงสัญญาณมูลค่าจริงตามเวลานั้น ไม่มีการพึ่งพาคุณค่าในอนาคตหรือในอดีต ดังนั้นจึงไม่ใช่ระบบไดนามิก แต่เป็นระบบคงที่

c) $y(t) = Even[x(t)]$

$$= \frac{[x(t)+x(-t)]}{2}$$

ที่นี่ถ้าเราจะแทนที่ t = 1 สัญญาณหนึ่งจะแสดง x (1) และอีกสัญญาณหนึ่งจะแสดง x (-1) ซึ่งเป็นค่าที่ผ่านมา ในทำนองเดียวกันถ้าเราใส่ t = -1 สัญญาณหนึ่งจะแสดง x (-1) และอีกสัญญาณหนึ่งจะแสดง x (1) ซึ่งเป็นค่าในอนาคต ดังนั้นชัดเจนว่าเป็นกรณีของระบบไดนามิก

d) $y(t) = \cos [x(t)]$

ในกรณีนี้เนื่องจากระบบเป็นฟังก์ชันโคไซน์จึงมีโดเมนค่าหนึ่งซึ่งอยู่ระหว่าง -1 ถึง +1 ดังนั้นค่าใดก็ตามที่เราใส่เราจะได้ผลลัพธ์ภายในขีด จำกัด ที่กำหนด ดังนั้นจึงเป็นระบบคงที่

จากตัวอย่างข้างต้นเราสามารถสรุปได้ดังนี้ -

สัญญาณกรณีการเปลี่ยนเวลาทั้งหมดเป็นสัญญาณแบบไดนามิก
ในกรณีของการปรับขนาดเวลาสัญญาณทั้งหมดเป็นสัญญาณไดนามิก
สัญญาณกรณีการรวมเป็นสัญญาณแบบไดนามิก

ก่อนหน้านี้เราเห็นว่าระบบจำเป็นต้องเป็นอิสระจากอนาคตและค่าในอดีตเพื่อให้เป็นแบบคงที่ ในกรณีนี้สภาพเกือบจะเหมือนเดิมโดยมีการปรับเปลี่ยนเพียงเล็กน้อย ที่นี่เพื่อให้ระบบเป็นเหตุเป็นผลควรเป็นอิสระจากค่าในอนาคตเท่านั้น นั่นหมายความว่าการพึ่งพาในอดีตจะทำให้ระบบไม่กลายเป็นสาเหตุ

ระบบสาเหตุเป็นระบบที่สามารถทำได้จริงหรือในทางกายภาพ ให้เราพิจารณาตัวอย่างบางส่วนเพื่อทำความเข้าใจสิ่งนี้ให้ดีขึ้น

ตัวอย่าง

ให้เราพิจารณาสัญญาณต่อไปนี้

a) $y(t) = x(t)$

ที่นี่สัญญาณขึ้นอยู่กับค่าปัจจุบันของ x เท่านั้น ตัวอย่างเช่นถ้าเราแทนที่ t = 3 ผลลัพธ์จะแสดงเฉพาะช่วงเวลานั้นเท่านั้น ดังนั้นเนื่องจากไม่มีการพึ่งพามูลค่าในอนาคตเราจึงเรียกมันว่าระบบสาเหตุ

b) $y(t) = x(t-1)$

ที่นี่ระบบขึ้นอยู่กับค่าในอดีต ตัวอย่างเช่นถ้าเราแทนที่ t = 3 นิพจน์จะลดเป็น x (2) ซึ่งเป็นค่าที่ผ่านมาเทียบกับอินพุตของเรา ไม่ว่าจะขึ้นอยู่กับมูลค่าในอนาคต ดังนั้นระบบนี้จึงเป็นระบบเชิงสาเหตุด้วย

c) $y(t) = x(t)+x(t+1)$

ในกรณีนี้ระบบมีสองส่วน ส่วน x (t) ตามที่เราได้กล่าวไปก่อนหน้านี้ขึ้นอยู่กับค่าปัจจุบันเท่านั้น ดังนั้นไม่มีปัญหากับมัน อย่างไรก็ตามถ้าเราใช้กรณีของ x (t + 1) มันขึ้นอยู่กับค่าในอนาคตอย่างชัดเจนเพราะถ้าเราใส่ t = 1 นิพจน์จะลดเป็น x (2) ซึ่งเป็นค่าในอนาคต ดังนั้นจึงไม่ใช่สาเหตุ

ระบบที่ไม่ใช่สาเหตุนั้นตรงข้ามกับระบบสาเหตุ หากระบบขึ้นอยู่กับค่าในอนาคตของอินพุตในช่วงเวลาใดเวลาหนึ่งระบบจะกล่าวว่าเป็นระบบที่ไม่ใช่สาเหตุ

ตัวอย่าง

ให้เราใช้ตัวอย่างและพยายามทำความเข้าใจในทางที่ดีขึ้น

a) $y(t) = x(t+1)$

เราได้พูดถึงระบบนี้แล้วในระบบเชิงสาเหตุด้วย สำหรับอินพุตใด ๆ ระบบจะลดมูลค่าของระบบในอนาคต ตัวอย่างเช่นถ้าเราใส่ t = 2 มันจะลดเป็น x (3) ซึ่งเป็นค่าในอนาคต ดังนั้นระบบจึงไม่ใช่สาเหตุ

b) $y(t) = x(t)+x(t+2)$

ในกรณีนี้ x (t) เป็นฟังก์ชันที่ขึ้นกับมูลค่าปัจจุบันเท่านั้น เราได้พูดคุยกันแล้วว่าฟังก์ชัน x (t + 2) ขึ้นอยู่กับอนาคตเพราะสำหรับ t = 3 จะให้ค่าสำหรับ x (5) ดังนั้นจึงไม่ใช่สาเหตุ

c) $y(t) = x(t-1)+x(t)$

ในระบบนี้ขึ้นอยู่กับค่าปัจจุบันและในอดีตของอินพุตที่กำหนด ไม่ว่าเราจะทดแทนค่าอะไรก็ตามมันจะไม่แสดงการพึ่งพาในอนาคต เห็นได้ชัดว่ามันไม่ใช่ระบบที่ไม่ใช่สาเหตุ ค่อนข้างเป็นระบบสาเหตุ

ระบบต่อต้านสาเหตุเป็นเพียงเวอร์ชันที่แก้ไขเล็กน้อยของระบบที่ไม่ใช่สาเหตุ ระบบขึ้นอยู่กับค่าในอนาคตของอินพุตเท่านั้น ไม่มีการพึ่งพาทั้งในปัจจุบันหรือค่าในอดีต

ตัวอย่าง

ค้นหาว่าระบบต่อไปนี้ต่อต้านสาเหตุหรือไม่

a) $y(t) = x(t)+x(t-1)$

ระบบมีฟังก์ชันย่อยสองฟังก์ชัน ฟังก์ชันย่อยหนึ่งฟังก์ชัน x (t + 1) ขึ้นอยู่กับค่าในอนาคตของอินพุต แต่ฟังก์ชันย่อยอื่น x (t) ขึ้นอยู่กับปัจจุบันเท่านั้น เนื่องจากระบบขึ้นอยู่กับมูลค่าปัจจุบันนอกเหนือจากมูลค่าในอนาคตระบบนี้จึงไม่ได้ต่อต้านสาเหตุ

b) $y(t) = x(t+3)$

ถ้าเราวิเคราะห์ระบบข้างต้นเราจะเห็นว่าระบบขึ้นอยู่กับค่าในอนาคตของระบบเท่านั้นคือถ้าเราใส่ t = 0 มันจะลดเป็น x (3) ซึ่งเป็นค่าในอนาคต ระบบนี้เป็นตัวอย่างที่สมบูรณ์แบบของระบบต่อต้านสาเหตุ

ระบบเชิงเส้นเป็นไปตามกฎของการซ้อนทับ กฎหมายนี้เป็นเงื่อนไขที่จำเป็นและเพียงพอในการพิสูจน์ความเป็นเชิงเส้นของระบบ นอกเหนือจากนี้ระบบยังรวมกฎหมายสองประเภทเข้าด้วยกัน -

กฎแห่งการเสพติด
กฎแห่งความเป็นเนื้อเดียวกัน

ทั้งสองกฎแห่งความเป็นเนื้อเดียวกันและกฎแห่งการเติมแต่งแสดงไว้ในรูปด้านบน อย่างไรก็ตามมีเงื่อนไขอื่น ๆ เพื่อตรวจสอบว่าระบบเป็นแบบเส้นตรงหรือไม่

The conditions are -

เอาต์พุตควรเป็นศูนย์สำหรับอินพุตเป็นศูนย์
ไม่ควรมีตัวดำเนินการที่ไม่ใช่เชิงเส้นอยู่ในระบบ

ตัวอย่างของตัวดำเนินการที่ไม่ใช่เชิงเส้น -

(a) ตัวดำเนินการตรีโกณมิติ - Sin, Cos, Tan, Cot, Sec, Cosec เป็นต้น

(b) เอกซ์โพเนนเชียลลอการิทึมโมดูลัสสี่เหลี่ยมลูกบาศก์เป็นต้น

อินพุต x หรือเอาต์พุต y ไม่ควรมีตัวดำเนินการที่ไม่ใช่เชิงเส้นเหล่านี้

ตัวอย่าง

ให้เราตรวจสอบว่าระบบต่อไปนี้เป็นเชิงเส้นหรือไม่

a) $y(t) = x(t)+3$

ระบบนี้ไม่ใช่ระบบเชิงเส้นเนื่องจากละเมิดเงื่อนไขแรก ถ้าเราใส่อินพุตเป็นศูนย์ทำให้ x (t) = 0 แสดงว่าเอาต์พุตไม่เป็นศูนย์

b) $y(t) = \sin tx(t)$

ในระบบนี้ถ้าเราให้อินพุตเป็นศูนย์เอาต์พุตจะกลายเป็นศูนย์ ดังนั้นเงื่อนไขแรกคือความพึงพอใจอย่างชัดเจน อีกครั้งไม่มีตัวดำเนินการที่ไม่ใช่เชิงเส้นที่ใช้กับ x (t) ดังนั้นเงื่อนไขที่สองก็พอใจเช่นกัน ดังนั้นระบบจึงเป็นระบบเชิงเส้น

c) $y(t) = \sin (x(t))$

ในระบบข้างต้นเงื่อนไขแรกเป็นที่พอใจเพราะถ้าเราใส่ x (t) = 0 ผลลัพธ์ก็จะเป็น sin (0) = 0 เช่นกันอย่างไรก็ตามเงื่อนไขที่สองไม่เป็นที่พอใจเนื่องจากมีตัวดำเนินการที่ไม่ใช่เชิงเส้นซึ่ง ดำเนินการ x (t) ดังนั้นระบบจึงไม่เป็นเส้นตรง

ถ้าเราต้องการกำหนดระบบนี้เราสามารถพูดได้ว่าระบบที่ไม่ใช่เชิงเส้นเป็นระบบที่ไม่ใช่เชิงเส้น เห็นได้ชัดว่าเงื่อนไขทั้งหมดที่ถูกละเมิดในระบบเชิงเส้นควรเป็นที่พอใจในกรณีนี้

เงื่อนไข

เอาต์พุตไม่ควรเป็นศูนย์เมื่ออินพุตที่ใช้เป็นศูนย์
สามารถใช้ตัวดำเนินการที่ไม่ใช่เชิงเส้นกับอินพุตหรือเอาต์พุตเพื่อทำให้ระบบไม่เป็นเชิงเส้น

ตัวอย่าง

เพื่อดูว่าระบบที่กำหนดเป็นแบบเส้นตรงหรือไม่เป็นเส้นตรง

a) $y(t) = e^{x(t)}$

ในระบบข้างต้นเงื่อนไขแรกเป็นที่พอใจเพราะถ้าเราทำให้อินพุตเป็นศูนย์ผลลัพธ์คือ 1 นอกจากนี้ตัวดำเนินการที่ไม่ใช่เชิงเส้นแบบเอ็กซ์โพเนนเชียลจะถูกนำไปใช้กับอินพุต เห็นได้ชัดว่าเป็นกรณีของระบบ Non-Linear

b) $y(t) = x(t+1)+x(t-1)$

ระบบประเภทข้างต้นเกี่ยวข้องกับคุณค่าทั้งในอดีตและในอนาคต อย่างไรก็ตามหากเราจะทำให้อินพุตเป็นศูนย์แสดงว่าไม่มีค่าใดเลย ดังนั้นเราสามารถพูดได้ว่าหากอินพุตเป็นศูนย์ดังนั้นเวลาที่ปรับขนาดและเวอร์ชันที่เลื่อนเวลาของอินพุตจะเป็นศูนย์ด้วยซึ่งละเมิดเงื่อนไขแรกของเรา อีกครั้งไม่มีตัวดำเนินการที่ไม่ใช่เชิงเส้น ดังนั้นจึงมีการละเมิดเงื่อนไขที่สองด้วย เห็นได้ชัดว่าระบบนี้ไม่ใช่ระบบที่ไม่ใช่เชิงเส้น ค่อนข้างเป็นระบบเชิงเส้น

สำหรับระบบที่ไม่แปรผันตามเวลาเอาต์พุตและอินพุตควรล่าช้าออกไปโดยหน่วยเวลาบางส่วน ความล่าช้าใด ๆ ที่ระบุในอินพุตจะต้องสะท้อนให้เห็นในเอาต์พุตสำหรับระบบที่ไม่แปรผันตามเวลา

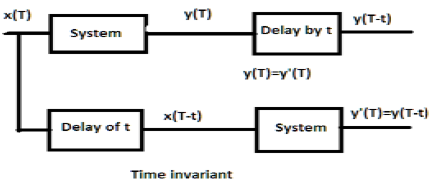
ตัวอย่าง

a) $y(T) = x(2T)$

หากนิพจน์ข้างต้นจะถูกส่งผ่านระบบก่อนแล้วจึงผ่านการหน่วงเวลา (ดังแสดงในส่วนบนของรูป) จากนั้นผลลัพธ์จะกลายเป็น$x(2T-2t)$. ตอนนี้นิพจน์เดียวกันจะถูกส่งผ่านการหน่วงเวลาก่อนแล้วจึงผ่านระบบ (ดังแสดงในส่วนล่างของรูป) ผลลัพธ์จะกลายเป็น$x(2T-t)$.

ดังนั้นระบบไม่ใช่ระบบที่ไม่แปรผันตามเวลา

b) $y(T) = \sin [x(T)]$

หากสัญญาณถูกส่งผ่านระบบก่อนจากนั้นผ่านกระบวนการหน่วงเวลาเอาต์พุตจะเป็น $\sin x(T-t)$. ในทำนองเดียวกันถ้าระบบถูกส่งผ่านการหน่วงเวลาก่อนจากนั้นผ่านระบบเอาต์พุตจะเป็น$\sin x(T-t)$. เราจะเห็นได้อย่างชัดเจนว่าเอาต์พุตทั้งสองเหมือนกัน ดังนั้นระบบจึงไม่แปรผันตามเวลา

สำหรับระบบตัวแปรเวลาเอาต์พุตและอินพุตควรล่าช้าออกไปโดยค่าคงที่ของเวลาบางส่วน แต่ความล่าช้าที่อินพุตไม่ควรสะท้อนที่เอาต์พุต กรณีมาตราส่วนเวลาทั้งหมดเป็นตัวอย่างของระบบตัวแปรเวลา ในทำนองเดียวกันเมื่อค่าสัมประสิทธิ์ในความสัมพันธ์ของระบบเป็นฟังก์ชันของเวลาระบบก็จะแปรผันตามเวลา

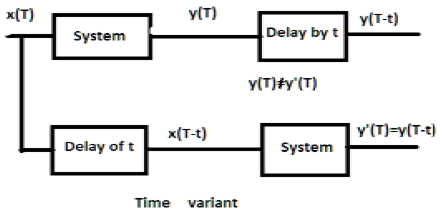
ตัวอย่าง

a) $y(t) = x[\cos T]$

หากสัญญาณข้างต้นถูกส่งผ่านระบบก่อนจากนั้นผ่านการหน่วงเวลาเอาต์พุตจะเป็น $x\cos (T-t)$. หากผ่านการหน่วงเวลาก่อนแล้วจึงผ่านระบบจะเป็น$x(\cos T-t)$. เนื่องจากเอาต์พุตไม่เหมือนกันระบบจึงเป็นตัวแปรตามเวลา

b) $y(T) = \cos T.x(T)$

หากนิพจน์ข้างต้นถูกส่งผ่านระบบก่อนและจากนั้นผ่านการหน่วงเวลาผลลัพธ์จะเป็น $\cos(T-t)x(T-t)$. อย่างไรก็ตามหากนิพจน์ถูกส่งผ่านการหน่วงเวลาก่อนแล้วจึงผ่านระบบเอาต์พุตจะเป็น$\cos T.x(T-t)$. เนื่องจากเอาต์พุตไม่เหมือนกันระบบจึงเป็นตัวแปรตามเวลา

ระบบที่เสถียรเป็นไปตามเงื่อนไข BIBO (อินพุทที่กำหนดขอบเขตสำหรับเอาต์พุตที่มีขอบเขต) ในที่นี้หมายถึงขอบเขต จำกัด ในแอมพลิจูด สำหรับระบบที่มีเสถียรภาพเอาต์พุตควรมีขอบเขตหรือ จำกัด สำหรับอินพุต จำกัด หรือขอบเขตในทุกช่วงเวลา

ตัวอย่างบางส่วนของอินพุทแบบมีขอบเขตคือฟังก์ชันของไซน์โคไซน์ DC เครื่องหมายและขั้นตอนของหน่วย

ตัวอย่าง

a) $y(t) = x(t)+10$

ที่นี่สำหรับอินพุตขอบเขตที่แน่นอนเราสามารถรับเอาต์พุตแบบกำหนดขอบเขตที่แน่นอนได้เช่นถ้าเราใส่ $x(t) = 2, y(t) = 12$ซึ่งมีขอบเขตอยู่ในธรรมชาติ ดังนั้นระบบจึงมีความเสถียร

b) $y(t) = \sin [x(t)]$

ในนิพจน์ที่กำหนดเรารู้ว่าฟังก์ชันไซน์มีขอบเขตของค่าที่แน่นอนซึ่งอยู่ระหว่าง -1 ถึง +1 ดังนั้นค่าใดก็ตามที่เราจะแทนที่ด้วย x (t) เราจะได้ค่าภายในขอบเขตของเรา ดังนั้นระบบจึงมีความเสถียร

ระบบที่ไม่เสถียรไม่เป็นไปตามเงื่อนไข BIBO ดังนั้นสำหรับอินพุตที่มีขอบเขตเราไม่สามารถคาดหวังเอาต์พุตที่มีขอบเขตได้ในกรณีของระบบที่ไม่เสถียร

ตัวอย่าง

a) $y(t) = tx(t)$

ที่นี่สำหรับอินพุต จำกัด เราไม่สามารถคาดหวังผลลัพธ์ที่ จำกัด ได้ ตัวอย่างเช่นถ้าเราจะใส่$x(t) = 2 \Rightarrow y(t) = 2t$. นี่ไม่ใช่ค่า จำกัด เพราะเราไม่รู้ค่า t ดังนั้นจึงสามารถอยู่ได้จากทุกที่ ดังนั้นระบบนี้จึงไม่เสถียร มันเป็นระบบที่ไม่เสถียร

b) $y(t) = \frac{x(t)}{\sin t}$

เราได้พูดคุยกันก่อนหน้านี้ว่าฟังก์ชันไซน์มีช่วงที่แน่นอนตั้งแต่ -1 ถึง +1; แต่ที่นี่มีอยู่ในตัวส่วน ดังนั้นในกรณีที่เลวร้ายที่สุดถ้าเราใส่ t = 0 และฟังก์ชันไซน์กลายเป็นศูนย์ระบบทั้งหมดจะไม่มีที่สิ้นสุด ดังนั้นระบบประเภทนี้จึงไม่เสถียรเลย เห็นได้ชัดว่านี่เป็นระบบที่ไม่เสถียร

Example 1 - ตรวจสอบว่า $y(t) = x*(t)$ เป็นเส้นตรงหรือไม่เป็นเส้นตรง

Solution- ฟังก์ชันแสดงถึงคอนจูเกตของอินพุต สามารถตรวจสอบได้โดยกฎข้อแรกของความเป็นเนื้อเดียวกันและกฎแห่งการเติมแต่งหรือโดยกฎสองข้อ อย่างไรก็ตามการยืนยันผ่านกฎนั้นง่ายกว่ามากดังนั้นเราจะดำเนินการตามนั้น

หากอินพุตไปยังระบบเป็นศูนย์เอาต์พุตก็มีแนวโน้มที่จะเป็นศูนย์เช่นกัน ดังนั้นเงื่อนไขแรกของเราคือความพึงพอใจ ไม่มีตัวดำเนินการที่ไม่ใช่เชิงเส้นที่ใช้ที่อินพุตหรือเอาต์พุต ดังนั้นระบบจึงเป็น Linear

Example 2 - ตรวจสอบว่า $y(t)=\begin{cases}x(t+1), & t > 0\\x(t-1), & t\leq 0\end{cases}$ เป็นเส้นตรงหรือไม่เป็นเส้นตรง

Solution- เห็นได้ชัดว่าเมื่อเวลาน้อยกว่าหรือเท่ากับศูนย์อินพุตจะกลายเป็นศูนย์ ดังนั้นเราสามารถพูดได้ว่าที่อินพุตเป็นศูนย์ผลลัพธ์ก็เป็นศูนย์เช่นกันและเงื่อนไขแรกของเราก็พอใจแล้ว

อีกครั้งไม่มีตัวดำเนินการที่ไม่ใช่เชิงเส้นที่ใช้ที่อินพุตหรือที่เอาต์พุต ดังนั้นระบบจึงเป็น Linear

Example 3 - ตรวจสอบว่า $y(t) = \sin t.x(t)$ มีความเสถียรหรือไม่

Solution - สมมติว่าเรานำค่า x (t) เป็น 3 ที่นี่ฟังก์ชันไซน์ถูกคูณด้วยและค่าสูงสุดและต่ำสุดของฟังก์ชันไซน์จะแตกต่างกันระหว่าง -1 ถึง +1

ดังนั้นค่าสูงสุดและต่ำสุดของฟังก์ชันทั้งหมดจะแตกต่างกันไประหว่าง -3 ถึง +3 ดังนั้นระบบจึงมีเสถียรภาพเนื่องจากที่นี่เราได้รับอินพุตแบบขอบเขตสำหรับเอาต์พุตที่มีขอบเขต

Discrete Time Fourier Transform (DTFT) มีไว้สำหรับสัญญาณพลังงานและพลังงาน Z-transform ยังมีอยู่สำหรับสัญญาณประเภทพลังงานหรือพลังงาน (NENP) ในระดับหนึ่งเท่านั้น การเปลี่ยน$z=e^{jw}$ ใช้สำหรับการแปลง Z เป็น DTFT สำหรับสัญญาณที่สรุปได้เท่านั้น

ดังนั้นการแปลง Z ของสัญญาณเวลาที่ไม่ต่อเนื่อง x (n) ในอนุกรมกำลังจึงสามารถเขียนเป็น -

$$X(z) = \sum_{n-\infty}^\infty x(n)Z^{-n}$$

สมการข้างต้นแสดงสมการแปลง Z สองด้าน

โดยทั่วไปเมื่อสัญญาณถูกแปลงเป็น Z มันสามารถแสดงเป็น -

$$X(Z) = Z[x(n)]$$

หรือ $x(n) \longleftrightarrow X(Z)$

หากเป็นสัญญาณเวลาต่อเนื่องก็ไม่จำเป็นต้องใช้การแปลง Z เนื่องจากใช้การแปลงลาปลาซ อย่างไรก็ตามสัญญาณเวลาไม่ต่อเนื่องสามารถวิเคราะห์ได้ผ่านการแปลง Z เท่านั้น

ภูมิภาคของการบรรจบกัน

Region of Convergence คือช่วงของตัวแปร Z ที่ซับซ้อนในระนาบ Z การแปลง Z ของสัญญาณนั้น จำกัด หรือบรรจบกัน ดังนั้น ROC จึงแสดงถึงชุดค่าของ Z ซึ่ง X (Z) มีค่า จำกัด

คุณสมบัติของ ROC

ROC ไม่รวมเสาใด ๆ
สำหรับสัญญาณด้านขวา ROC จะอยู่นอกวงกลมในระนาบ Z
สำหรับสัญญาณด้านซ้าย ROC จะอยู่ในวงกลมในระนาบ Z
เพื่อความเสถียร ROC รวมวงกลมหน่วยในระนาบ Z
สำหรับสัญญาณทั้งสองด้าน ROC เป็นวงแหวนในระนาบ Z
สำหรับสัญญาณระยะเวลา จำกัด ROC คือระนาบ Z ทั้งหมด

Z-transform มีลักษณะเฉพาะคือ -

การแสดงออกของ X (Z)
ROC ของ X (Z)

สัญญาณและ ROC

x (n)	X (Z)	ร็อค
$\delta(n)$	$1$	เครื่องบิน Z ทั้งหมด
$U(n)$	$1/(1-Z^{-1})$	Mod (Z)> 1
$a^nu(n)$	$1/(1-aZ^{-1})$	มอด (Z)> มอด (ก)
$-a^nu(-n-1)$	$1/(1-aZ^{-1})$	Mod (Z) <Mod (a)
$na^nu(n)$	$aZ^{-1}/(1-aZ^{-1})^2$	มอด (Z)> มอด (ก)
$-a^nu(-n-1)$	$aZ^{-1}/(1-aZ^{-1})^2$	Mod (Z) <Mod (a)
$U(n)\cos \omega n$	$(Z^2-Z\cos \omega)/(Z^2-2Z \cos \omega +1)$	Mod (Z)> 1
$U(n)\sin \omega n$	$(Z\sin \omega)/(Z^2-2Z \cos \omega +1)$	Mod (Z)> 1

ตัวอย่าง

ให้เราหา Z-transform และ ROC ของสัญญาณที่กำหนดให้เป็น $x(n) = \lbrace 7,3,4,9,5\rbrace$โดยจุดกำเนิดของซีรีส์อยู่ที่ 3

Solution - ใช้สูตรที่เรามี -

$X(z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$

$= \sum_{n=-1}^3 x(n)Z^{-n}$

$= x(-1)Z+x(0)+x(1)Z^{-1}+x(2)Z^{-2}+x(3)Z^{-3}$

$= 7Z+3+4Z^{-1}+9Z^{-2}+5Z^{-3}$

ROC คือระนาบ Z ทั้งหมดยกเว้น Z = 0, ∞, -∞

ในบทนี้เราจะเข้าใจคุณสมบัติพื้นฐานของการแปลง Z

ความเป็นเส้นตรง

ระบุว่าเมื่อสัญญาณที่ไม่ต่อเนื่องสองสัญญาณหรือมากกว่านั้นคูณด้วยค่าคงที่การแปลง Z ตามลำดับจะถูกคูณด้วยค่าคงที่เดียวกัน

ในทางคณิตศาสตร์

$$a_1x_1(n)+a_2x_2(n) = a_1X_1(z)+a_2X_2(z)$$

Proof - เรารู้ว่า

$$X(Z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$$

$= \sum_{n=-\infty}^\infty (a_1x_1(n)+a_2x_2(n))Z^{-n}$

$= a_1\sum_{n = -\infty}^\infty x_1(n)Z^{-n}+a_2\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$

$= a_1X_1(z)+a_2X_2(z)$ (จึงพิสูจน์แล้ว)

ที่นี่ ROC คือ $ROC_1\bigcap ROC_2$.

การเปลี่ยนเวลา

คุณสมบัติการเปลี่ยนเวลาแสดงให้เห็นว่าการเปลี่ยนแปลงของโดเมนเวลาในสัญญาณไม่ต่อเนื่องจะส่งผลต่อโดเมน Z ซึ่งสามารถเขียนเป็น;

$$x(n-n_0)\longleftrightarrow X(Z)Z^{-n}$$

หรือ $x(n-1)\longleftrightarrow Z^{-1}X(Z)$

Proof -

ปล่อย $y(P) = X(P-K)$

$Y(z) = \sum_{p = -\infty}^\infty y(p)Z^{-p}$

$= \sum_{p = -\infty}^\infty (x(p-k))Z^{-p}$

ให้ s = pk

$= \sum_{s = -\infty}^\infty x(s)Z^{-(s+k)}$

$= \sum_{s = -\infty}^\infty x(s)Z^{-s}Z^{-k}$

$= Z^{-k}[\sum_{s=-\infty}^\infty x(m)Z^{-s}]$

$= Z^{-k}X(Z)$ (จึงพิสูจน์แล้ว)

ที่นี่ ROC สามารถเขียนเป็น Z = 0 (p> 0) หรือ Z = ∞ (p <0)

ตัวอย่าง

U (n) และ U (n-1) สามารถลงจุดได้ดังนี้

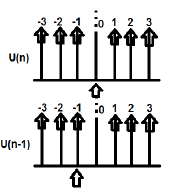
Z-transformation ของ U (n) cab เขียนเป็น;

$\sum_{n = -\infty}^\infty [U(n)]Z^{-n} = 1$

การแปลง Z ของ U (n-1) สามารถเขียนเป็น;

$\sum_{n = -\infty}^\infty [U(n-1)]Z^{-n} = Z^{-1}$

ที่นี่ $x(n-n_0) = Z^{-n_0}X(Z)$ (จึงพิสูจน์แล้ว)

การปรับเวลา

คุณสมบัติ Time Scaling บอกเราว่าโดเมน Z ของสัญญาณจะเป็นอย่างไรเมื่อเวลาถูกปรับขนาดในรูปแบบไม่ต่อเนื่องซึ่งสามารถเขียนเป็น;

$$a^nx(n) \longleftrightarrow X(a^{-1}Z)$$

Proof -

ปล่อย $y(p) = a^{p}x(p)$

$Y(P) = \sum_{p=-\infty}^\infty y(p)Z^{-p}$

$= \sum_{p=-\infty}^\infty a^px(p)Z^{-p}$

$= \sum_{p=-\infty}^\infty x(p)[a^{-1}Z]^{-p}$

$= X(a^{-1}Z)$(จึงพิสูจน์แล้ว)

ROC: = Mod (ar1) <Mod (Z) <Mod (ar2) โดยที่ Mod = Modulus

ตัวอย่าง

ให้เราตรวจสอบการแปลง Z ของ $x(n) = a^n \cos \omega n$ โดยใช้คุณสมบัติการปรับเวลา

Solution -

เรารู้แล้วว่าการแปลง Z ของสัญญาณ $\cos (\omega n)$ ให้โดย -

$$\sum_{n=-\infty}^\infty(\cos \omega n)Z^{-n} = (Z^2-Z \cos \omega)/(Z^2-2Z\cos \omega +1)$$

ตอนนี้ใช้คุณสมบัติ Time scaling การแปลง Z ของ $a^n \cos \omega n$ สามารถเขียนเป็น;

$\sum_{n=-\infty}^\infty(a^n\cos \omega n)Z^{-n} = X(a^{-1}Z)$

$= [(a^{-1}Z)^2-(a^{-1}Z \cos \omega n)]/((a^{-1}Z)^2-2(a^{-1}Z \cos \omega n)+1)$

$= Z(Z-a \cos \omega)/(Z^2-2az \cos \omega+a^2)$

ความแตกต่างอย่างต่อเนื่อง

คุณสมบัติความแตกต่างแบบต่อเนื่องแสดงให้เห็นว่าการแปลง Z จะเกิดขึ้นเมื่อเราแยกความแตกต่างของสัญญาณที่ไม่ต่อเนื่องในโดเมนเวลาตามเวลา ดังแสดงด้านล่าง

$$\frac{dx(n)}{dn} = (1-Z^{-1})X(Z)$$

Proof -

พิจารณา LHS ของสมการ - $\frac{dx(n)}{dn}$

$$= \frac{[x(n)-x(n-1)]}{[n-(n-1)]}$$

$= x(n)-X(n-1)$

$= x(Z)-Z^{-1}x(Z)$

$= (1-Z^{-1})x(Z)$ (จึงพิสูจน์แล้ว)

ROC: R1 <Mod (Z) <R2

ตัวอย่าง

ให้เราค้นหาการแปลง Z ของสัญญาณที่กำหนดโดย $x(n) = n^2u(n)$

ตามคุณสมบัติเราสามารถเขียน

$Zz[nU(n)] = -Z\frac{dZ[U(n)]}{dz}$

$= -Z\frac{d[\frac{Z}{Z-1}]}{dZ}$

$= Z/((Z-1)^2$

$= y(let)$

ตอนนี้ Z [ny] สามารถพบได้โดยการใช้คุณสมบัติอีกครั้ง

$Z(n,y) = -Z\frac{dy}{dz}$

$= -Z\frac{d[Z/(Z-1)^3]}{dz}$

$= Z(Z+1)/(Z-1)^2$

การแปลง

สิ่งนี้แสดงให้เห็นถึงการเปลี่ยนแปลงในโดเมน Z ของระบบเมื่อเกิด Convolution ในรูปแบบสัญญาณที่ไม่ต่อเนื่องซึ่งสามารถเขียนเป็น -

$x_1(n)*x_2(n) \longleftrightarrow X_1(Z).X_2(Z)$

Proof -

$X(Z) = \sum_{n = -\infty}^\infty x(n)Z^{-n}$

$= \sum_{n=-\infty}^\infty[\sum_{k = -\infty}^\infty x_1(k)x_2(n-k)]Z^{-n}$

$= \sum_{k = -\infty}^\infty x_1(k)[\sum_n^\infty x_2(n-k)Z^{-n}]$

$= \sum_{k = -\infty}^\infty x_1(k)[\sum_{n = -\infty}^\infty x_2(n-k)Z^{-(n-k)}Z^{-k}]$

ให้ nk = l จากนั้นสมการด้านบนจะเขียนเป็น -

$X(Z) = \sum_{k = -\infty}^\infty x_1(k)[Z^{-k}\sum_{l=-\infty}^\infty x_2(l)Z^{-l}]$

$= \sum_{k = -\infty}^\infty x_1(k)X_2(Z)Z^{-k}$

$= X_2(Z)\sum_{k = -\infty}^\infty x_1(Z)Z^{-k}$

$= X_1(Z).X_2(Z)$ (จึงพิสูจน์แล้ว)

ร็อค:$ROC\bigcap ROC2$

ตัวอย่าง

ให้เราค้นหาการประชุมที่ได้รับจากสัญญาณสองสัญญาณ

$x_1(n) = \lbrace 3,-2,2\rbrace$ ... (อค. 1)

$x_2(n) = \lbrace 2,0\leq 4\quad and\quad 0\quad elsewhere\rbrace$ ... (อค. 2)

การแปลง Z ของสมการแรกสามารถเขียนเป็น;

$\sum_{n = -\infty}^\infty x_1(n)Z^{-n}$

$= 3-2Z^{-1}+2Z^{-2}$

การแปลง Z ของสัญญาณที่สองสามารถเขียนเป็น;

$\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$

$= 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$

ดังนั้นการแปลงสัญญาณทั้งสองข้างต้นจะได้รับโดย -

$X(Z) = [x_1(Z)^*x_2(Z)]$

$= [3-2Z^{-1}+2Z^{-2}]\times [2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}]$

$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+...\quad...\quad...$

การแปลง Z แบบผกผันที่เราได้รับ

$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$

ทฤษฎีบทค่าเริ่มต้น

ถ้า x (n) เป็นลำดับเชิงสาเหตุซึ่งมีการแปลง Z เป็น X (z) ดังนั้นทฤษฎีบทค่าเริ่มต้นสามารถเขียนเป็น;

$X(n)(at\quad n = 0) = \lim_{z \to \infty} X(z)$

Proof - เรารู้ว่า

$X(Z) = \sum_{n = 0} ^\infty x(n)Z^{-n}$

ขยายชุดด้านบนเราได้รับ;

$= X(0)Z^0+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$

$= X(0)\times 1+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$

ในกรณีข้างต้นถ้า Z →∞แล้ว $Z^{-n}\rightarrow 0$ (เพราะ n> 0)

ดังนั้นเราสามารถพูด;

$\lim_{z \to \infty}X(z) = X(0)$ (จึงพิสูจน์แล้ว)

ทฤษฎีบทมูลค่าสุดท้าย

ทฤษฎีบทค่าสุดท้ายระบุว่าหากการแปลง Z ของสัญญาณแสดงเป็น X (Z) และเสาทั้งหมดอยู่ในวงกลมค่าสุดท้ายจะแสดงเป็น x (n) หรือ X (∞) และสามารถเขียนเป็น -

$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$

Conditions -

ใช้ได้กับระบบเชิงสาเหตุเท่านั้น
$X(Z)(1-Z^{-1})$ ควรมีเสาภายในวงกลมหน่วยในระนาบ Z

Proof - เรารู้ว่า

$Z^+[x(n+1)-x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$

$\Rightarrow Z^+[x(n+1)]-Z^+[x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$

$\Rightarrow Z[X(Z)^+-x(0)]-X(Z)^+ = \lim_{k \to \infty}\sum_{n = 0}^kZ^{-n}[x(n+1)-x(n)]$

ที่นี่เราสามารถใช้คุณสมบัติขั้นสูงของการแปลง Z ด้านเดียวได้ ดังนั้นสมการข้างต้นสามารถเขียนใหม่ได้เป็น;

$Z^+[x(n+1)] = Z[X(2)^+-x(0)Z^0] = Z[X(Z)^+-x(0)]$

ตอนนี้ใส่ z = 1 ในสมการข้างบนเราสามารถขยายสมการข้างบนได้ -

$\lim_{k \to \infty}{[x(1)-x(0)+x(6)-x(1)+x(3)-x(2)+...\quad...\quad...+x(x+1)-x(k)]}$

สามารถกำหนดเป็น;

$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$(จึงพิสูจน์แล้ว)

ตัวอย่าง

ให้เราหาค่าเริ่มต้นและค่าสุดท้ายของ x (n) ซึ่งสัญญาณถูกกำหนดโดย

$X(Z) = 2+3Z^{-1}+4Z^{-2}$

Solution - อันดับแรกให้เราหาค่าเริ่มต้นของสัญญาณโดยใช้ทฤษฎีบท

$x(0) = \lim_{z \to \infty}X(Z)$

$= \lim_{z \to \infty}[2+3Z^{-1}+4Z^{-2}]$

$= 2+(\frac{3}{\infty})+(\frac{4}{\infty}) = 2$

ตอนนี้ให้เราหาค่าสุดท้ายของสัญญาณที่ใช้ทฤษฎีบท

$x(\infty) = \lim_{z \to \infty}[(1-Z^{-1})X(Z)]$

$= \lim_{z \to \infty}[(1-Z^{-1})(2+3Z^{-1}+4Z^{-2})]$

$= \lim_{z \to \infty}[2+Z^{-1}+Z^{-2}-4Z^{-3}]$

$= 2+1+1-4 = 0$

Some other properties of Z-transform are listed below -

ความแตกต่างของความถี่

มันทำให้เกิดการเปลี่ยนแปลงในโดเมน Z ของสัญญาณเมื่อสัญญาณที่ไม่ต่อเนื่องแตกต่างกันไปตามเวลา

$nx(n)\longleftrightarrow -Z\frac{dX(z)}{dz}$

ROC สามารถเขียนเป็น;

$r_2< Mod(Z)< r_1$

ตัวอย่าง

ให้เราหาค่าของ x (n) ผ่านความแตกต่างของความถี่ซึ่งสัญญาณที่ไม่ต่อเนื่องในโดเมน Z ได้รับ $x(n)\longleftrightarrow X(Z) = log(1+aZ^{-1})$

ตามคุณสมบัติเราสามารถเขียนได้

$nx(n)\longleftrightarrow -Z\frac{dx(Z)}{dz}$

$= -Z[\frac{-aZ^{-2}}{1+aZ^{-1}}]$

$= (aZ^{-1})/(1+aZ^{-1})$

$= 1-1/(1+aZ^{-1})$

$nx(n) = \delta(n)-(-a)^nu(n)$

$\Rightarrow x(n) = 1/n[\delta(n)-(-a)^nu(n)]$

การคูณในเวลา

จะให้การเปลี่ยนแปลงในโดเมน Z ของสัญญาณเมื่อการคูณเกิดขึ้นที่ระดับสัญญาณไม่ต่อเนื่อง

$x_1(n).x_2(n)\longleftrightarrow(\frac{1}{2\Pi j})[X1(Z)*X2(Z)]$

การผันเวลา

สิ่งนี้แสดงถึงการเป็นตัวแทนของสัญญาณที่ไม่ต่อเนื่องผันในโดเมน Z

$X^*(n)\longleftrightarrow X^*(Z^*)$

ระบบที่มีฟังก์ชันของระบบจะมีเสถียรภาพได้ก็ต่อเมื่อเสาทั้งหมดอยู่ในวงกลมยูนิตเท่านั้น ขั้นแรกให้ตรวจสอบว่าระบบมีสาเหตุหรือไม่ หากระบบเป็นสาเหตุเราจะทำการกำหนดความเสถียรของ BIBO โดยที่ความเสถียรของ BIBO หมายถึงอินพุตที่มีขอบเขตสำหรับเงื่อนไขเอาต์พุตที่มีขอบเขต

สามารถเขียนเป็น;

$Mod(X(Z))< \infty$

$= Mod(\sum x(n)Z^{-n})< \infty$

$= \sum Mod(x(n)Z^{-n})< \infty$

$= \sum Mod[x(n)(re^{jw})^{-n}]< 0$

$= \sum Mod[x(n)r^{-n}]Mod[e^{-jwn}]< \infty$

$= \sum_{n = -\infty}^\infty Mod[x(n)r^{-n}]< \infty$

สมการข้างต้นแสดงเงื่อนไขการดำรงอยู่ของการแปลง Z

อย่างไรก็ตามเงื่อนไขสำหรับการมีอยู่ของสัญญาณ DTFT คือ

$$\sum_{n = -\infty}^\infty Mod(x(n)< \infty$$

ตัวอย่าง 1

ให้เราลองหา Z-transform ของสัญญาณซึ่งได้รับเป็น

$x(n) = -(-0.5)^{-n}u(-n)+3^nu(n)$

$= -(-2)^nu(n)+3^nu(n)$

Solution - ที่นี่สำหรับ $-(-2)^nu(n)$ ROC อยู่ด้านซ้ายและ Z <2

สำหรับ $3^nu(n)$ ROC อยู่ด้านขวาและ Z> 3

ดังนั้นที่นี่ Z-transform ของสัญญาณจะไม่มีอยู่เนื่องจากไม่มีภูมิภาคทั่วไป

ตัวอย่าง 2

ให้เราลองหา Z-transform ของสัญญาณที่กำหนด

$x(n) = -2^nu(-n-1)+(0.5)^nu(n)$

Solution - ที่นี่สำหรับ $-2^nu(-n-1)$ ROC ของสัญญาณอยู่ด้านซ้ายและ Z <2

สำหรับสัญญาณ $(0.5)^nu(n)$ ROC อยู่ด้านขวาและ Z> 0.5

ดังนั้น ROC ทั่วไปจึงถูกสร้างขึ้นเป็น 0.5 <Z <2

ดังนั้น Z-transform สามารถเขียนเป็น;

$X(Z) = \lbrace\frac{1}{1-2Z^{-1}}\rbrace+\lbrace\frac{1}{(1-0.5Z)^{-1}}\rbrace$

ตัวอย่างที่ 3

ให้เราลองหา Z-transform ของสัญญาณซึ่งได้รับเป็น $x(n) = 2^{r(n)}$

Solution- r (n) คือสัญญาณทางลาด ดังนั้นสัญญาณสามารถเขียนเป็น;

$x(n) = 2^{nu(n)}\lbrace 1, n<0 (u(n)=0)\quad and\quad2^n, n\geq 0(u(n) = 1)\rbrace$

$= u(-n-1)+2^nu(n)$

ที่นี่สำหรับสัญญาณ $u(-n-1)$ และ ROC Z <1 และสำหรับ $2^nu(n)$ กับ ROC คือ Z> 2

ดังนั้นจะไม่มีการแปลงสัญญาณ Z ของสัญญาณ

Z -Transform สำหรับระบบสาเหตุ

ระบบสาเหตุสามารถกำหนดเป็น $h(n) = 0,n<0$. สำหรับระบบเชิงสาเหตุ ROC จะอยู่นอกวงกลมในระนาบ Z

$H(Z) = \displaystyle\sum\limits_{n = 0}^{\infty}h(n)Z^{-n}$

ขยายสมการข้างต้น

$H(Z) = h(0)+h(1)Z^{-1}+h(2)Z^{-2}+...\quad...\quad...$

$= N(Z)/D(Z)$

สำหรับระบบเชิงสาเหตุการขยายฟังก์ชัน Transfer ไม่รวมพลังบวกของ Z สำหรับระบบเชิงสาเหตุลำดับของตัวเศษต้องไม่เกินลำดับของตัวส่วน สามารถเขียนเป็น -

$\lim_{z \rightarrow \infty}H(Z) = h(0) = 0\quad or\quad Finite$

เพื่อความเสถียรของระบบสาเหตุเสาของฟังก์ชัน Transfer ควรอยู่ในวงกลมหน่วยในระนาบ Z

Z-transform สำหรับระบบต่อต้านสาเหตุ

ระบบต่อต้านสาเหตุสามารถกำหนดเป็น $h(n) = 0, n\geq 0$. สำหรับระบบต่อต้านสาเหตุเสาของฟังก์ชันการถ่ายโอนควรอยู่นอกวงกลมหน่วยในระนาบ Z สำหรับระบบต่อต้านสาเหตุ ROC จะอยู่ในวงกลมในระนาบ Z

หากเราต้องการวิเคราะห์ระบบซึ่งแสดงอยู่แล้วในโดเมนความถี่เป็นสัญญาณเวลาที่ไม่ต่อเนื่องเราก็ไปหา Inverse Z-transformation

ในทางคณิตศาสตร์สามารถแสดงเป็น;

$$x(n) = Z^{-1}X(Z)$$

โดยที่ x (n) เป็นสัญญาณในโดเมนเวลาและ X (Z) คือสัญญาณในโดเมนความถี่

หากเราต้องการแสดงสมการข้างต้นในรูปแบบอินทิกรัลเราสามารถเขียนเป็น

$$x(n) = (\frac{1}{2\Pi j})\oint X(Z)Z^{-1}dz$$

ที่นี่อินทิกรัลอยู่บนเส้นทางปิด C เส้นทางนี้อยู่ภายใน ROC ของ x (z) และมีจุดกำเนิด

วิธีค้นหา Inverse Z-Transform

เมื่อต้องการการวิเคราะห์ในรูปแบบไม่ต่อเนื่องเราจะแปลงสัญญาณโดเมนความถี่กลับเป็นรูปแบบไม่ต่อเนื่องผ่านการแปลง Z แบบผกผัน เราทำตามสี่วิธีต่อไปนี้เพื่อพิจารณาการแปลง Z แบบผกผัน

วิธีการหารยาว
วิธีการขยายเศษส่วนบางส่วน
วิธีการอินทิกรัลที่เหลือหรือคอนทัวร์

วิธีการหารยาว

ในวิธีนี้การแปลง Z ของสัญญาณ x (z) สามารถแสดงเป็นอัตราส่วนของพหุนามดังที่แสดงด้านล่าง

$$x(z)=N(Z)/D(Z)$$

ทีนี้ถ้าเราหารเศษด้วยตัวส่วนเราจะได้อนุกรมดังที่แสดงด้านล่าง

$$X(z) = x(0)+x(1)Z^{-1}+x(2)Z^{-2}+...\quad...\quad...$$

ลำดับข้างต้นแสดงถึงชุดของการแปลง Z แบบผกผันของสัญญาณที่กำหนด (สำหรับn≥0) และระบบข้างต้นเป็นสาเหตุ

อย่างไรก็ตามสำหรับ n <0 อนุกรมสามารถเขียนเป็น;

$$x(z) = x(-1)Z^1+x(-2)Z^2+x(-3)Z^3+...\quad...\quad...$$

วิธีการขยายเศษส่วนบางส่วน

ที่นี่สัญญาณจะแสดงก่อนในรูปแบบ N (z) / D (z)

ถ้าเป็นเศษส่วนอย่างมีเหตุผลจะแสดงดังนี้

$x(z) = b_0+b_1Z^{-1}+b_2Z^{-2}+...\quad...\quad...+b_mZ^{-m})/(a_0+a_1Z^{-1}+a_2Z^{-2}+...\quad...\quad...+a_nZ^{-N})$

ข้อใดข้อหนึ่งไม่เหมาะสมเมื่อ m <n และ≠ 0

หากอัตราส่วนไม่เหมาะสม (เช่นไม่เหมาะสม) เราต้องแปลงเป็นรูปแบบที่เหมาะสมเพื่อแก้ปัญหา

วิธีการที่เหลือหรือ Contour Integral

ในวิธีนี้เราจะได้ค่าผกผัน Z-transform x (n) โดยการรวมส่วนที่เหลือของ $[x(z)Z^{n-1}]$ที่เสาทั้งหมด ในทางคณิตศาสตร์สิ่งนี้อาจแสดงเป็น

$$x(n) = \displaystyle\sum\limits_{all\quad poles\quad X(z)}residues\quad of[x(z)Z^{n-1}]$$

ที่นี่กากสำหรับขั้วใด ๆ ของคำสั่ง m ที่ $z = \beta$ คือ

$$Residues = \frac{1}{(m-1)!}\lim_{Z \rightarrow \beta}\lbrace \frac{d^{m-1}}{dZ^{m-1}}\lbrace (z-\beta)^mX(z)Z^{n-1}\rbrace$$

ตัวอย่าง 1

ค้นหาการตอบสนองของระบบ $s(n+2)-3s(n+1)+2s(n) = \delta (n)$เมื่อเงื่อนไขเริ่มต้นทั้งหมดเป็นศูนย์

Solution - เราได้การแปลง Z ทั้งสองข้างของสมการข้างต้น

$$S(z)Z^2-3S(z)Z^1+2S(z) = 1$$

$\Rightarrow S(z)\lbrace Z^2-3Z+2\rbrace = 1$

$\Rightarrow S(z) = \frac{1}{\lbrace z^2-3z+2\rbrace}=\frac{1}{(z-2)(z-1)} = \frac{\alpha _1}{z-2}+\frac{\alpha _2}{z-1}$

$\Rightarrow S(z) = \frac{1}{z-2}-\frac{1}{z-1}$

เราได้การแปลง Z แบบผกผันของสมการข้างต้น

$S(n) = Z^{-1}[\frac{1}{Z-2}]-Z^{-1}[\frac{1}{Z-1}]$

$= 2^{n-1}-1^{n-1} = -1+2^{n-1}$

ตัวอย่าง 2

ค้นหาฟังก์ชันระบบ H (z) และการตอบสนองตัวอย่างหน่วย h (n) ของระบบที่มีการอธิบายสมการความแตกต่างไว้ภายใต้

$y(n) = \frac{1}{2}y(n-1)+2x(n)$

โดยที่ y (n) และ x (n) คือเอาต์พุตและอินพุตของระบบตามลำดับ

Solution - เราได้การแปลง Z ของสมการความแตกต่างข้างต้น

$y(z) = \frac{1}{2}Z^{-1}Y(Z)+2X(z)$

$= Y(Z)[1-\frac{1}{2}Z^{-1}] = 2X(Z)$

$= H(Z) = \frac{Y(Z)}{X(Z)} = \frac{2}{[1-\frac{1}{2}Z^{-1}]}$

ระบบนี้มีเสาอยู่ที่ $Z = \frac{1}{2}$ และ $Z = 0$ และ $H(Z) = \frac{2}{[1-\frac{1}{2}Z^{-1}]}$

ดังนั้นเราจึงได้การแปลง Z แบบผกผันของข้างต้น

$h(n) = 2(\frac{1}{2})^nU(n)$

ตัวอย่างที่ 3

กำหนด Y (z), n≥0ในกรณีต่อไปนี้ -

$y(n)+\frac{1}{2}y(n-1)-\frac{1}{4}y(n-2) = 0\quad given\quad y(-1) = y(-2) = 1$

Solution - ใช้ Z-transform กับสมการข้างต้นเราจะได้รับ

$Y(Z)+\frac{1}{2}[Z^{-1}Y(Z)+Y(-1)]-\frac{1}{4}[Z^{-2}Y(Z)+Z^{-1}Y(-1)+4(-2)] = 0$

$\Rightarrow Y(Z)+\frac{1}{2Z}Y(Z)+\frac{1}{2}-\frac{1}{4Z^2}Y(Z)-\frac{1}{4Z}-\frac{1}{4} = 0$

$\Rightarrow Y(Z)[1+\frac{1}{2Z}-\frac{1}{4Z^2}] =\frac{1}{4Z}-\frac{1}{2}$

$\Rightarrow Y(Z)[\frac{4Z^2+2Z-1}{4Z^2}] = \frac{1-2Z}{4Z}$

$\Rightarrow Y(Z) = \frac{Z(1-2Z)}{4Z^2+2Z-1}$

เช่นเดียวกับการแปลงฟูเรียร์ของสัญญาณเวลาต่อเนื่องการแปลงฟูริเยร์แบบไม่ต่อเนื่องสามารถใช้เพื่อแสดงลำดับที่ไม่ต่อเนื่องในการแสดงโดเมนความถี่เทียบเท่าและระบบเวลาแยก LTI และพัฒนาอัลกอริทึมการคำนวณต่างๆ

X (jω) ใน FT ต่อเนื่องเป็นฟังก์ชันต่อเนื่องของ x (n) อย่างไรก็ตาม DFT เกี่ยวข้องกับการแทนค่า x (n) ด้วยตัวอย่างของสเปกตรัม X (ω) ดังนั้นเครื่องมือทางคณิตศาสตร์นี้จึงมีความสำคัญอย่างมากในการคำนวณในการนำเสนอที่สะดวก ทั้งสองลำดับเป็นระยะและไม่เป็นระยะสามารถประมวลผลผ่านเครื่องมือนี้ ลำดับคาบจำเป็นต้องสุ่มตัวอย่างโดยการขยายระยะเวลาเป็นอนันต์

การสุ่มตัวอย่างโดเมนความถี่

จากบทนำเป็นที่ชัดเจนว่าเราจำเป็นต้องรู้วิธีดำเนินการผ่านการสุ่มตัวอย่างโดเมนความถี่เช่นการสุ่มตัวอย่าง X (ω) ดังนั้นความสัมพันธ์ระหว่างการแปลงฟูเรียร์ตัวอย่างและ DFT จึงถูกสร้างขึ้นในลักษณะต่อไปนี้

ในทำนองเดียวกันลำดับคาบก็สามารถปรับให้พอดีกับเครื่องมือนี้ได้โดยการขยายช่วงเวลา N เป็นอนันต์

ให้ลำดับที่ไม่ใช่คาบเป็น $X(n) = \lim_{N \to \infty}x_N(n)$

การกำหนดการแปลงฟูเรียร์

$X(\omega ) = \sum_{n=-\infty}^\infty x(n)e^{-jwn}X(K\delta \omega)$

ที่นี่ X (ω) จะถูกสุ่มตัวอย่างเป็นระยะ ๆ ทุกช่วงเรเดียน

เนื่องจาก X (ω) เป็นระยะใน2πเรเดียนเราจึงต้องการตัวอย่างในช่วงพื้นฐานเท่านั้น ตัวอย่างจะถูกนำมาหลังจากช่วงเวลาที่เท่ากันในช่วงความถี่0≤ω≤2π ระยะห่างระหว่างช่วงเวลาที่เท่ากันคือ$\delta \omega = \frac{2\pi }{N}k$ เรเดียน.

ตอนนี้กำลังประเมิน $\omega = \frac{2\pi}{N}k$

$X(\frac{2\pi}{N}k) = \sum_{n = -\infty}^\infty x(n)e^{-j2\pi nk/N},$ ... eq (2)

โดยที่ k = 0,1, …… N-1

หลังจากแบ่งย่อยข้างต้นและเปลี่ยนลำดับของการสรุป

$X(\frac{2\pi}{N}k) = \displaystyle\sum\limits_{n = 0}^{N-1}[\displaystyle\sum\limits_{l = -\infty}^\infty x(n-Nl)]e^{-j2\pi nk/N}$ ... eq (3)

$\sum_{l=-\infty}^\infty x(n-Nl) = x_p(n) = a\quad periodic\quad function\quad of\quad period\quad N\quad and\quad its\quad fourier\quad series\quad = \sum_{k = 0}^{N-1}C_ke^{j2\pi nk/N}$

โดยที่ n = 0,1, … .. , N-1; 'p'- ย่อมาจาก periodic entity หรือ function

สัมประสิทธิ์ฟูเรียร์คือ

$C_k = \frac{1}{N}\sum_{n = 0}^{N-1}x_p(n)e^{-j2\pi nk/N}$k = 0,1, …, N-1 ... eq (4)

การเปรียบเทียบสมการ 3 และ 4 เราได้

$NC_k = X(\frac{2\pi}{N}k)$k = 0,1, …, N-1 ... eq (5)

$NC_k = X(\frac{2\pi}{N}k) = X(e^{jw}) = \displaystyle\sum\limits_{n = -\infty}^\infty x_p(n)e^{-j2\pi nk/N}$... eq (6)

จากการขยายชุดฟูเรียร์

$x_p(n) = \frac{1}{N}\displaystyle\sum\limits_{k = 0}^{N-1}NC_ke^{j2\pi nk/N} = \frac{1}{N}\sum_{k = 0}^{N-1}X(\frac{2\pi}{N}k)e^{j2\pi nk/N}$... eq (7)

โดยที่ n = 0,1, …, N-1

ที่นี่เราได้รับสัญญาณเป็นระยะจาก X (ω) $x(n)$ สามารถสกัดได้จาก $x_p(n)$ เฉพาะในกรณีที่ไม่มีนามแฝงในโดเมนเวลา $N\geq L$

N = ระยะเวลาของ $x_p(n)$ L = ระยะเวลาของ $x(n)$

$x(n) = \begin{cases}x_p(n), & 0\leq n\leq N-1\\0, & Otherwise\end{cases}$

การทำแผนที่ทำได้ในลักษณะนี้

คุณสมบัติของ DFT

ความเป็นเส้นตรง

ระบุว่า DFT ของสัญญาณรวมกันเท่ากับผลรวมของ DFT ของแต่ละสัญญาณ ให้เรารับสัญญาณสองตัว x ₁ (n) และ x ₂ (n) ซึ่ง DFT s คือ X ₁ (ω) และ X ₂ (ω) ตามลำดับ ดังนั้นถ้า

$x_1(n)\rightarrow X_1(\omega)$และ$x_2(n)\rightarrow X_2(\omega)$

แล้ว $ax_1(n)+bx_2(n)\rightarrow aX_1(\omega)+bX_2(\omega)$

ที่ไหน a และ b คือค่าคงที่

สมมาตร

คุณสมบัติสมมาตรของ DFT สามารถหาได้ในลักษณะเดียวกับที่เราได้รับคุณสมบัติสมมาตร DTFT เรารู้ว่า DFT ของลำดับ x (n) แสดงด้วย X (K) ตอนนี้ถ้า x (n) และ X (K) เป็นลำดับที่มีค่าเชิงซ้อนก็จะแสดงเป็นด้านล่างได้

$x(n) = x_R(n)+jx_1(n),0\leq n\leq N-1$

และ $X(K) = X_R(K)+jX_1(K),0\leq K\leq N-1$

คุณสมบัติคู่

ให้เราพิจารณาสัญญาณ x (n) ซึ่ง DFT ได้รับเป็น X (K) ให้ลำดับระยะเวลา จำกัด เป็น X (N) จากนั้นตามทฤษฎีบทความเป็นคู่

ถ้า, $x(n)\longleftrightarrow X(K)$

จากนั้น $X(N)\longleftrightarrow Nx[((-k))_N]$

ดังนั้นโดยการใช้ทฤษฎีบทนี้ถ้าเรารู้ DFT เราสามารถค้นหาลำดับระยะเวลา จำกัด ได้อย่างง่ายดาย

คุณสมบัติคอนจูเกตที่ซับซ้อน

สมมติว่ามีสัญญาณ x (n) ซึ่ง DFT รู้จักกันในชื่อ X (K) ตอนนี้ถ้าคอนจูเกตที่ซับซ้อนของสัญญาณถูกกำหนดให้เป็น x * (n) เราสามารถค้นหา DFT ได้อย่างง่ายดายโดยไม่ต้องคำนวณมากโดยใช้ทฤษฎีบทที่แสดงด้านล่าง

ถ้า, $x(n)\longleftrightarrow X(K)$

จากนั้น $x*(n)\longleftrightarrow X*((K))_N = X*(N-K)$

การเปลี่ยนความถี่แบบวงกลม

การคูณของลำดับ x (n) ด้วยลำดับเลขชี้กำลังที่ซับซ้อน $e^{j2\Pi kn/N}$เทียบเท่ากับการเลื่อนแบบวงกลมของ DFT โดยหน่วย L ในความถี่ นี่คือคุณสมบัติการเปลี่ยนเวลาแบบคู่เป็นวงกลม

ถ้า, $x(n)\longleftrightarrow X(K)$

จากนั้น $x(n)e^{j2\Pi Kn/N}\longleftrightarrow X((K-L))_N$

การคูณสองลำดับ

หากมีสัญญาณสองสัญญาณ x ₁ (n) และ x ₂ (n) และ DFT ตามลำดับคือ X ₁ (k) และ X ₂ (K) การคูณสัญญาณตามลำดับเวลาจะสอดคล้องกับการแปลงแบบวงกลมของ DFT

ถ้า, $x_1(n)\longleftrightarrow X_1(K)\quad\&\quad x_2(n)\longleftrightarrow X_2(K)$

ทฤษฎีบทของ Parseval

สำหรับลำดับค่าที่ซับซ้อน x (n) และ y (n) โดยทั่วไป

ถ้า, $x(n)\longleftrightarrow X(K)\quad \&\quad y(n)\longleftrightarrow Y(K)$

จากนั้น $\sum_{n = 0}^{N-1}x(n)y^*(n) = \frac{1}{N}\sum_{k = 0}^{N-1}X(K)Y^*(K)$

เรารู้ว่าเมื่อ $\omega = 2\pi K/N$ และ $N\rightarrow \infty,\omega$ กลายเป็นตัวแปรต่อเนื่องและผลรวมขีด จำกัด จะกลายเป็น $-\infty$ ถึง $+\infty$.

ดังนั้น,

$$NC_k = X(\frac{2\pi}{N}k) = X(e^{j\omega}) = \displaystyle\sum\limits_{n = -\infty}^\infty x(n)e^{\frac{-j2\pi nk}{N}} = \displaystyle\sum\limits_{n = -\infty}^\infty x(n)e^{-j\omega n}$$

การแปลงฟูริเยร์แบบไม่ต่อเนื่อง (DTFT)

เรารู้ว่า, $X(e^{j\omega}) = \sum_{n = -\infty}^\infty x(n)e^{-j\omega n}$

ที่ไหน $X(e^{j\omega})$มีความต่อเนื่องและเป็นระยะในωและมีคาบ2π … eq (1)

ตอนนี้

$x_p(n) = \sum_{k = 0}^{N-1}NC_ke^{j2 \pi nk/N}$ …จากอนุกรมฟูริเยร์

$x_p(n) = \frac{1}{2\pi}\sum_{k=0}^{N-1}NC_ke^{j2\pi nk/N}\times \frac{2\pi}{N}$

ωกลายเป็นแบบต่อเนื่องและ $\frac{2\pi}{N}\rightarrow d\omega$เนื่องจากเหตุผลที่อ้างถึงข้างต้น

$x(n) = \frac{1}{2\pi}\int_{n = 0}^{2\pi}X(e^{j\omega})e^{j\omega n}d\omega$… eq (2)

การแปลงฟูเรียร์เวลาไม่ต่อเนื่องผกผัน

ในเชิงสัญลักษณ์

$x(n)\Longleftrightarrow x(e^{j\omega})$(คู่ Fourier Transform)

เงื่อนไขที่จำเป็นและเพียงพอสำหรับการคงอยู่ของการแปลงฟูริเยร์แบบไม่ต่อเนื่องสำหรับลำดับที่ไม่ใช่คาบ x (n) นั้นสามารถสรุปได้แน่นอน

กล่าวคือ$\sum_{n = -\infty}^\infty|x(n)|<\infty$

คุณสมบัติของ DTFT

Linearity : $a_1x_1(n)+a_2x_2(n)\Leftrightarrow a_1X_1(e^{j\omega})+a_2X_2(e^{j\omega})$
Time shifting - $x(n-k)\Leftrightarrow e^{-j\omega k}.X(e^{j\omega})$
Time Reversal - $x(-n)\Leftrightarrow X(e^{-j\omega})$
Frequency shifting - $e^{j\omega _0n}x(n)\Leftrightarrow X(e^{j(\omega -\omega _0)})$
Differentiation frequency domain - $nx(n) = j\frac{d}{d\omega}X(e^{j\omega})$
Convolution - $x_1(n)*x_2(n)\Leftrightarrow X_1(e^{j\omega})\times X_2(e^{j\omega})$
Multiplication - $x_1(n)\times x_2(n)\Leftrightarrow X_1(e^{j\omega})*X_2(e^{j\omega})$
Co-relation - $y_{x_1\times x_2}(l)\Leftrightarrow X_1(e^{j\omega})\times X_2(e^{j\omega})$
Modulation theorem - $x(n)\cos \omega _0n = \frac{1}{2}[X_1(e^{j(\omega +\omega _0})*X_2(e^{jw})$
Symmetry -$x^*(n)\Leftrightarrow X^*(e^{-j\omega})$ ;

$x^*(-n)\Leftrightarrow X^*(e^{j\omega})$ ;

$Real[x(n)]\Leftrightarrow X_{even}(e^{j\omega})$ ;

$Imag[x(n)]\Leftrightarrow X_{odd}(e^{j\omega})$ ;

$x_{even}(n)\Leftrightarrow Real[x(e^{j\omega})]$ ;

$x_{odd}(n)\Leftrightarrow Imag[x(e^{j\omega})]$ ;
Parseval’s theorem - $\sum_{-\infty}^\infty|x_1(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X_1(e^{j\omega})|^2d\omega$

ก่อนหน้านี้เราศึกษาการสุ่มตัวอย่างในโดเมนความถี่ ด้วยความรู้พื้นฐานนั้นเราจึงเป็นตัวอย่าง$X(e^{j\omega})$ในโดเมนความถี่เพื่อให้สามารถทำการวิเคราะห์แบบดิจิทัลได้อย่างสะดวกจากข้อมูลตัวอย่างนั้น ดังนั้น DFT จึงถูกสุ่มตัวอย่างทั้งในโดเมนเวลาและความถี่ ด้วยสมมติฐาน$x(n) = x_p(n)$

ดังนั้น DFT จึงถูกกำหนดโดย -

$X(k) = DFT[x(n)] = X(\frac{2\pi}{N}k) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{-\frac{j2\pi nk}{N}}$, k = 0,1, …., N − 1 … eq (3)

และ IDFT มอบให้โดย -

$X(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k = 0}^{N-1}X(k)e^{\frac{j2\pi nk}{N}}$, n = 0,1, …., N − 1 … eq (4)

$\therefore x(n)\Leftrightarrow X(k)$

ปัจจัย Twiddle

มันแสดงเป็น $W_N$ และกำหนดเป็น $W_N = e^{-j2\pi /N}$. ขนาดของมันยังคงอยู่ที่ความสามัคคีเสมอ เฟสของ$W_N = -2\pi /N$. เป็นเวกเตอร์บนวงกลมหน่วยและใช้เพื่อความสะดวกในการคำนวณ ในทางคณิตศาสตร์สามารถแสดงเป็น -

$W_N^r = W_N^{r\pm N} = W_N^{r\pm 2N} = ...$

มันเป็นฟังก์ชันของ r และจุด N

พิจารณา N = 8, r = 0,1,2,3, … .14,15,16, ….

$\Longleftrightarrow W_8^0 = W_8^8 = W_8^{16} = ... = ... = W_8^{32} = ... =1= 1\angle 0$
$W_8^1 = W_8^9 = W_8^{17} = ... = ... = W_8^{33} = ... =\frac{1}{\sqrt 2}= j\frac{1}{\sqrt 2} = 1\angle-\frac{\pi}{4}$

การแปลงเชิงเส้น

ให้เราเข้าใจการแปลงเชิงเส้น -

เรารู้ว่า,

$DFT(k) = DFT[x(n)] = X(\frac{2\pi}{N}k) = \sum_{n = 0}^{N-1}x(n).W_n^{-nk};\quad k = 0,1,….,N−1$

$x(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k = 0}^{N-1}X(k).W_N^{-nk};\quad n = 0,1,….,N−1$

Note- การคำนวณ DFT สามารถทำได้ด้วยการคูณเชิงซ้อนN ²และการบวกแบบซับซ้อน N (N-1)

$x_N = \begin{bmatrix}x(0)\\x(1)\\.\\.\\x(N-1) \end{bmatrix}\quad N\quad point\quad vector\quad of\quad signal\quad x_N$

$X_N = \begin{bmatrix}X(0)\\X(1)\\.\\.\\X(N-1) \end{bmatrix}\quad N\quad point\quad vector\quad of\quad signal\quad X_N$

$\begin{bmatrix}1 & 1 & 1 & ... & ... & 1\\1 & W_N & W_N^2 & ... & ... & W_N^{N-1}\\. & W_N^2 & W_N^4 & ... & ... & W_N^{2(N-1)}\\.\\1 & W_N^{N-1} & W_N^{2(N-1)} & ... & ... & W_N^{(N-1)(N-1)} \end{bmatrix}$

N - point DFT ในเมทริกซ์กำหนดโดย - $X_N = W_Nx_N$

$W_N\longmapsto$ เมทริกซ์ของการแปลงเชิงเส้น

$Now,\quad x_N = W_N^{-1}X_N$

IDFT ในรูปแบบ Matrix กำหนดโดย

$$x_N = \frac{1}{N}W_N^*X_N$$

เปรียบเทียบทั้งสองนิพจน์ของ $x_N,\quad W_N^{-1} = \frac{1}{N}W_N^*$ และ $W_N\times W_N^* = N[I]_{N\times N}$

ดังนั้น, $W_N$ คือเมทริกซ์การแปลงเชิงเส้นเมทริกซ์มุมฉาก (รวมกัน)

จากทรัพย์สินเป็นงวดของ $W_N$ และจากคุณสมบัติสมมาตรสรุปได้ว่า $W_N^{k+N/2} = -W_N^k$

สมมาตรแบบวงกลม

N-point DFT ของระยะเวลา จำกัด x (n) ของความยาวN≤Lเทียบเท่ากับ N-point DFT ของส่วนขยายเป็นระยะของ x (n) นั่นคือ $x_p(n)$ ของช่วงเวลา N. และ $x_p(n) = \sum_{l = -\infty}^\infty x(n-Nl)$. ตอนนี้ถ้าเราเลื่อนลำดับซึ่งเป็นลำดับคาบโดยหน่วย k ไปทางขวาจะได้ลำดับระยะอื่น สิ่งนี้เรียกว่า Circular shift และสิ่งนี้กำหนดโดย

$$x_p^\prime (n) = x_p(n-k) = \sum_{l = -\infty}^\infty x(n-k-Nl)$$

ลำดับ จำกัด ใหม่สามารถแสดงเป็น

$$x_p^\prime (n) = \begin{cases}x_p^\prime(n), & 0\leq n\leq N-1\\0 & Otherwise\end{cases}$$

Example - ให้ x (n) = {1,2,4,3}, N = 4,

$x_p^\prime (n) = x(n-k,modulo\quad N)\equiv x((n-k))_N\quad;ex-if\quad k=2i.e\quad 2\quad unit\quad right\quad shift\quad and\quad N = 4,$

ถือว่าทิศทางตามเข็มนาฬิกาเป็นทิศทางบวก

เราได้ $x\prime(n) = x((n-2))_4$

$x\prime(0) = x((-2))_4 = x(2) = 4$

$x\prime(1) = x((-1))_4 = x(3) = 3$

$x\prime(2) = x((-2))_4 = x(0) = 1$

$x\prime(3) = x((1))_4 = x(1) = 2$

Conclusion - การเลื่อนแบบวงกลมของลำดับจุด N เทียบเท่ากับการเลื่อนเชิงเส้นของส่วนขยายระยะเวลาและในทางกลับกัน

ลำดับแบบวงกลมสม่ำเสมอ - $x(N-n) = x(n),\quad 1\leq n\leq N-1$

$i.e.x_p(n) = x_p(-n) = x_p(N-n)$

ผันแม้ -$x_p(n) = x_p^*(N-n)$

ลำดับคี่แบบวงกลม - $x(N-n) = -x(n),\quad 1\leq n\leq N-1$

$i.e.x_p(n) = -x_p(-n) = -x_p(N-n)$

ผันคี่ - $x_p(n) = -x_p^*(N-n)$

ตอนนี้ $x_p(n) = x_{pe}+x_{po}(n)$, ที่ไหน,

$x_{pe}(n) = \frac{1}{2}[x_p(n)+x_p^*(N-n)]$

$x_{po}(n) = \frac{1}{2}[x_p(n)-x_p^*(N-n)]$

สำหรับสัญญาณจริง x (n)$X(k) = X^*(N-k)$

$X_R(k) = X_R(N-k)$

$X_l(k) = -X_l(N-k)$

$\angle X(k) = -\angle X(N-K)$

Time reversal- การย้อนกลับของกลุ่มตัวอย่างเกี่ยวกับ 0 ^THตัวอย่าง ให้เป็น;

$x((-n))_N = x(N-n),\quad 0\leq n\leq N-1$

การย้อนเวลาคือการวางแผนตัวอย่างของลำดับในทิศทางตามเข็มนาฬิกาเช่นสมมติว่าเป็นทิศทางเชิงลบ

คุณสมบัติที่สำคัญอื่น ๆ

คุณสมบัติ IDFT ที่สำคัญอื่น ๆ $x(n)\longleftrightarrow X(k)$

Time reversal - $x((-n))_N = x(N-n)\longleftrightarrow X((-k))_N = X(N-k)$
Circular time shift - $x((n-l))_N \longleftrightarrow X(k)e^{j2\pi lk/N}$
Circular frequency shift - $x(n)e^{j2\pi ln/N} \longleftrightarrow X((k-l))_N$
Complex conjugate properties -

$x^*(n)\longleftrightarrow X^*((-k))_N = X^*(N-k)\quad and$

$x^*((-n))_N = x^*(N-n)\longleftrightarrow X^*(-k)$
Multiplication of two sequence -

$x_1(n)\longleftrightarrow X_1(k)\quad and\quad x_2(n)\longleftrightarrow X_2(k)$

$\therefore x_1(n)x_2(n)\longleftrightarrow X_1(k)\quadⓃ X_2(k)$
Circular convolution - และการคูณสอง DFT

$x_1(k)\quad Ⓝ x_2(k) =\sum_{k = 0}^{N-1}x_1(n).x_2((m-n))_n,\quad m = 0,1,2,... .,N-1 $

$x_1(k)\quad Ⓝ x_2(k)\longleftrightarrow X_1(k).X_2(k)$
Circular correlation - ถ้า $x(n)\longleftrightarrow X(k)$ และ $y(n)\longleftrightarrow Y(k)$ จากนั้นมีลำดับสหสัมพันธ์ข้ามที่แสดงเป็น $\bar Y_{xy}$ ดังนั้น $\bar Y_{xy}(l) = \sum_{n = 0}^{N-1}x(n)y^*((n-l))_N = X(k).Y^*(k)$
Parseval’s Theorem - ถ้า $x(n)\longleftrightarrow X(k)$ และ $y(n)\longleftrightarrow Y(k)$;

$\displaystyle\sum\limits_{n = 0}^{N-1}x(n)y^*(n) = \frac{1}{N}\displaystyle\sum\limits_{n =0}^{N-1}X(k).Y^*(k)$

ให้เราใช้ลำดับระยะเวลา จำกัด สองลำดับ x ₁ (n) และ x ₂ (n) โดยมีความยาวจำนวนเต็มเป็น N DFT ของพวกเขาคือ X ₁ (K) และ X ₂ (K) ตามลำดับซึ่งแสดงไว้ด้านล่าง -

$$X_1(K) = \sum_{n = 0}^{N-1}x_1(n)e^{\frac{j2\Pi kn}{N}}\quad k = 0,1,2...N-1$$ $$X_2(K) = \sum_{n = 0}^{N-1}x_2(n)e^{\frac{j2\Pi kn}{N}}\quad k = 0,1,2...N-1$$

ตอนนี้เราจะพยายามหา DFT ของลำดับอื่น x ₃ (n) ซึ่งกำหนดให้เป็น X ₃ (K)

$X_3(K) = X_1(K)\times X_2(K)$

โดยการรับ IDFT ข้างต้นเราจะได้รับ

$x_3(n) = \frac{1}{N}\displaystyle\sum\limits_{n = 0}^{N-1}X_3(K)e^{\frac{j2\Pi kn}{N}}$

หลังจากแก้สมการข้างต้นในที่สุดเราก็ได้

$x_3(n) = \displaystyle\sum\limits_{m = 0}^{N-1}x_1(m)x_2[((n-m))_N]\quad m = 0,1,2...N-1$

จุดเปรียบเทียบ	การแปลงเชิงเส้น	การแปลงแบบวงกลม
ขยับ	การขยับเชิงเส้น	การขยับแบบวงกลม
ตัวอย่างในผลลัพธ์ Convolution	$N_1+N_2−1$	$Max(N_1,N_2)$
การค้นหาการตอบสนองของตัวกรอง	เป็นไปได้	เป็นไปได้โดยไม่มีช่องว่างภายใน

วิธีการแปลงแบบวงกลม

โดยทั่วไปมีสองวิธีซึ่งถูกนำมาใช้เพื่อดำเนินการ Convolution แบบวงกลมและคือ -

วิธีวงกลมศูนย์กลาง
วิธีการคูณเมทริกซ์

วิธีวงกลมศูนย์กลาง

ปล่อย $x_1(n)$ และ $x_2(n)$เป็นสองลำดับที่กำหนด ขั้นตอนตามมาสำหรับการวนรอบของ$x_1(n)$ และ $x_2(n)$ คือ

ใช้วงกลมสองวง พล็อต N ตัวอย่างของ$x_1(n)$ บนเส้นรอบวงของวงกลมด้านนอก (รักษาจุดต่อเนื่องระยะทางเท่ากัน) ในทิศทางทวนเข็มนาฬิกา
สำหรับการวางพล็อต $x_2(n)$พล็อต N ตัวอย่างของ $x_2(n)$ในทิศทางตามเข็มนาฬิกาบนวงกลมด้านในตัวอย่างเริ่มต้นวางไว้ที่จุดเดียวกับ 0 ^THตัวอย่าง$x_1(n)$
คูณตัวอย่างที่เกี่ยวข้องในสองวงกลมแล้วเพิ่มเพื่อให้ได้ผลลัพธ์
หมุนวงกลมด้านในทวนเข็มนาฬิกาทีละตัวอย่าง

วิธีการคูณเมทริกซ์

วิธีเมทริกซ์แสดงถึงสองลำดับที่กำหนด $x_1(n)$ และ $x_2(n)$ ในรูปแบบเมทริกซ์

หนึ่งในลำดับที่กำหนดจะถูกทำซ้ำโดยการเลื่อนแบบวงกลมของตัวอย่างทีละหนึ่งครั้งเพื่อสร้างเมทริกซ์ NXN
ลำดับอื่นจะแสดงเป็นเมทริกซ์คอลัมน์
การคูณของเมทริกซ์สองตัวให้ผลลัพธ์ของการแปลงแบบวงกลม

DFT ให้แนวทางอื่นในการแปลงโดเมนเวลา สามารถใช้เพื่อทำการกรองเชิงเส้นในโดเมนความถี่

ด้วยประการฉะนี้$Y(\omega) = X(\omega).H(\omega)\longleftrightarrow y(n)$.

ปัญหาในแนวทางโดเมนความถี่นี้คือ $Y(\omega)$, $X(\omega)$ และ $H(\omega)$เป็นฟังก์ชันต่อเนื่องของωซึ่งไม่เกิดผลสำหรับการคำนวณดิจิทัลบนคอมพิวเตอร์ อย่างไรก็ตาม DFT ให้รูปแบบตัวอย่างของรูปคลื่นเหล่านี้เพื่อแก้ปัญหาวัตถุประสงค์

ข้อดีคือการมีความรู้เกี่ยวกับเทคนิค DFT ที่เร็วกว่าเช่น FFT ทำให้สามารถพัฒนาอัลกอริทึมที่มีประสิทธิภาพในการคำนวณสูงขึ้นสำหรับการคำนวณคอมพิวเตอร์ดิจิทัลเมื่อเทียบกับวิธีโดเมนเวลา

พิจารณาลำดับระยะเวลาที่ จำกัด $[x(n) = 0,\quad for,n<0\quad and\quad n\geq L]$ (สมการทั่วไป) กระตุ้นตัวกรองเชิงเส้นด้วยการตอบสนองของแรงกระตุ้น $[h(n) = 0,\quad forn<0\quad and\quad n\geq M]$.

$$x(n)y(n)$$ $$output = y(n) = \sum_{k = 0}^{M-1}h(k).x(n-k)$$

จากการวิเคราะห์ Convolution เป็นที่ชัดเจนว่าระยะเวลาของ y (n) คือ L + M − 1

ในโดเมนความถี่

$$Y(\omega) = X(\omega).H(\omega)$$

ตอนนี้ $Y(\omega)$ เป็นฟังก์ชันต่อเนื่องของωและสุ่มตัวอย่างที่ชุดของความถี่ที่ไม่ต่อเนื่องพร้อมด้วยจำนวนตัวอย่างที่แตกต่างกันซึ่งจะต้องเท่ากับหรือเกิน $L+M-1$.

$$DFT\quad size = N\geq L+M-1$$

ด้วย $\omega = \frac{2\pi}{N}k$,

$Y(\omega) = X(k).H(k)$โดยที่ k = 0,1, …., N-1

โดยที่ X (k) และ H (k) คือ N-point DFTs ของ x (n) และ h (n) ตามลำดับ $x(n)\& h(n)$ ถูกบุด้วยศูนย์จนถึงความยาว N มันจะไม่บิดเบือนสเปกตรัมต่อเนื่อง $X(\omega)$ และ $H(\omega)$. ตั้งแต่$N\geq L+M-1$, N-point DFT ของลำดับเอาต์พุต y (n) เพียงพอที่จะแสดง y (n) ในโดเมนความถี่และข้อเท็จจริงเหล่านี้อนุมานได้ว่าการคูณของ N-point DFTs ของ X (k) และ H (k) ตามด้วยการคำนวณ ของ N-point IDFT ต้องให้ y (n)

นี่หมายความว่าการ Convolution วงกลม N จุดของ x (n) และ H (n) ที่มีช่องว่างภายในเป็นศูนย์เท่ากับการแปลงเชิงเส้นของ x (n) และ h (n)

ดังนั้น DFT สามารถใช้สำหรับการกรองเชิงเส้น

Caution - N ควรมากกว่าหรือเท่ากับเสมอ $L+M-1$. มิฉะนั้นเอฟเฟกต์นามแฝงจะทำให้ลำดับเอาต์พุตเสียหาย

สมมติว่าลำดับอินพุต x (n) ของระยะเวลาที่ยาวนานจะถูกประมวลผลด้วยระบบที่มีการตอบสนองอิมพัลส์ระยะเวลา จำกัด โดยการเชื่อมโยงสองลำดับ เนื่องจากการกรองเชิงเส้นที่ดำเนินการผ่าน DFT เกี่ยวข้องกับการดำเนินการกับบล็อกข้อมูลขนาดคงที่ลำดับการป้อนข้อมูลจะถูกแบ่งออกเป็นบล็อกข้อมูลขนาดคงที่ต่างกันก่อนการประมวลผล

จากนั้นบล็อกต่อเนื่องจะถูกประมวลผลทีละบล็อกและผลลัพธ์จะถูกรวมเข้าด้วยกันเพื่อสร้างผลลัพธ์สุทธิ

เนื่องจากการ Convolution ดำเนินการโดยการแบ่งลำดับการป้อนข้อมูลแบบยาวออกเป็นส่วนขนาดคงที่ต่างกันจึงเรียกว่าการแปลงแบบแบ่งส่วน ลำดับการป้อนข้อมูลแบบยาวจะแบ่งเป็นบล็อกขนาดคงที่ก่อนการประมวลผลตัวกรอง FIR

ใช้สองวิธีในการประเมิน Convolution แบบไม่ต่อเนื่อง -

Overlap-save method
Overlap-add method

วิธีการบันทึกทับซ้อนกัน

Overlap – save เป็นชื่อดั้งเดิมสำหรับวิธีที่มีประสิทธิภาพในการประเมิน Convolution แบบไม่ต่อเนื่องระหว่างสัญญาณที่ยาวมาก x (n) และฟิลเตอร์การตอบสนองอิมพัลส์ จำกัด (FIR) h (n) ด้านล่างนี้เป็นขั้นตอนของวิธีการบันทึกทับซ้อนกัน -

ให้ความยาวของบล็อกข้อมูลอินพุต = N = L + M-1 ดังนั้น DFT และ IDFT length = N แต่ละบล็อกข้อมูลมีจุดข้อมูล M-1 ของบล็อกก่อนหน้าตามด้วยจุดข้อมูลใหม่ L เพื่อสร้างลำดับข้อมูลของความยาว N = L + M-1

ขั้นแรกให้คำนวณ N-point DFT สำหรับแต่ละบล็อกข้อมูล
ด้วยการต่อท้ายศูนย์ (L-1) การตอบสนองแรงกระตุ้นของฟิลเตอร์ FIR จะเพิ่มความยาวและ N จุด DFT จะถูกคำนวณและจัดเก็บ
การคูณของสองจุด N-point DFTs H (k) และ X _m (k): Y ′ _m (k) = H (k) .X _m (k) โดยที่ K = 0,1,2, … N-1
จากนั้น IDFT [Y ′ _m ((k)] = y′ ((n) = [y ′ _m (0), y′ _m (1), y ′ _m (2), ....... y ′ _ม. (M-1), y′ _ม. (M), ....... y ′ _ม. (N-1)]

(ที่นี่ N-1 = L + M-2)
จุด M-1 แรกเสียหายเนื่องจากการใช้นามแฝงดังนั้นจึงถูกทิ้งเนื่องจากบันทึกข้อมูลมีความยาว N
จุด L สุดท้ายจะเหมือนกับผลของการแปลงดังนั้น

y ′ _m (n) = y _m (n) โดยที่ n = M, M + 1, … .N-1
เพื่อหลีกเลี่ยงการ aliasing, M-1 ที่ผ่านมาองค์ประกอบของแต่ละระเบียนข้อมูลจะถูกบันทึกและจุดเหล่านี้ดำเนินการส่งต่อไปยังระเบียนตามมาและกลายเป็น 1 ^{เซนต์} M-1 องค์ประกอบ

ผลลัพธ์ของ IDFT โดยที่จุด M-1 แรกถูกหลีกเลี่ยงเพื่อทำให้นามแฝงเป็นโมฆะและจุด L ที่เหลือจะทำให้ได้ผลลัพธ์ที่ต้องการเหมือนกับการแปลงเชิงเส้น

ซ้อนทับวิธีการเพิ่ม

ด้านล่างนี้เป็นขั้นตอนในการค้นหา Convolution แบบไม่ต่อเนื่องโดยใช้วิธี Overlap -

ให้ขนาดบล็อกข้อมูลอินพุตเป็น L ดังนั้นขนาดของ DFT และ IDFT: N = L + M-1

แต่ละบล็อกข้อมูลจะต่อท้ายด้วยเลขศูนย์ M-1 ต่อท้าย
คำนวณ N-point DFT

คูณ N-point DFT สองจุด: Y _m (k) = H (k) .X _m (k) โดยที่ k = 0,, 1,2, …., N-1
IDFT [Y _m (k)] สร้างบล็อกที่มีความยาว N ซึ่งไม่ได้รับผลกระทบจากการใช้นามแฝงเนื่องจากขนาดของ DFT คือ N = L + M-1 และเพิ่มความยาวของลำดับไปยังจุด N โดยการผนวกเลขศูนย์ M-1 เข้ากับแต่ละจุด บล็อก.
คะแนน M-1 สุดท้ายของแต่ละบล็อกจะต้องทับซ้อนกันและเพิ่มไปยังจุด M-1 แรกของบล็อกที่สำเร็จ

(เหตุผล: แต่ละบล็อกข้อมูลจะสิ้นสุดด้วยศูนย์ M-1)

ดังนั้นวิธีนี้จึงเรียกว่าวิธีการเพิ่มการซ้อนทับ ดังนั้นเราจึงได้รับ -

y (n) = {y ₁ (0), y ₁ (1), y ₁ (2), … .. , y ₁ (L-1), y ₁ (L) + y ₂ (0), y ₁ (L + 1) + y ₂ (1), ... … .. , y ₁ (N-1) + y ₂ (M-1), y ₂ (M), … .. . ... ... ... }

DCT (การแปลงโคไซน์แบบไม่ต่อเนื่อง) คือลำดับอินพุต N x (n), 0≤n≤N-1 เป็นการแปลงเชิงเส้นหรือการรวมกันของเลขชี้กำลังที่ซับซ้อน เป็นผลให้ค่าสัมประสิทธิ์ DFT โดยทั่วไปมีความซับซ้อนแม้ว่า x (n) จะเป็นจริง

สมมติว่าเราพยายามค้นหาการแปลงมุมฉากซึ่งมีโครงสร้าง N × N ที่แสดงลำดับจริง x (n) เป็นการรวมเชิงเส้นของลำดับโคไซน์ เรารู้แล้วว่า -

$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)cos\frac{2\Pi kn}{N}0\leq k \leq N-1$

และ $x(n) = \frac{1}{N}\sum_{k = 0}^{N-1}x(k)cos\frac{2\Pi kn}{N}0\leq k \leq N-1$

เป็นไปได้ถ้าลำดับจุด N x (n) เป็นจริงและสม่ำเสมอ ด้วยประการฉะนี้$x(n) = x(N-n),0\leq n \leq (N-1)$. DFT ที่ได้นั้นเป็นของจริงและสม่ำเสมอ สิ่งเหล่านี้ทำให้ชัดเจนว่าเราสามารถหาอุปกรณ์การแปลงโคไซน์แบบไม่ต่อเนื่องสำหรับลำดับจริง N จุดใดก็ได้โดยการใช้ DFT จุด 2N ของ "ส่วนขยายคู่" ของลำดับ

โดยพื้นฐานแล้ว DCT ใช้ในการประมวลผลภาพและคำพูด นอกจากนี้ยังใช้ในการบีบอัดภาพและสัญญาณเสียงพูด

$DFT[s(n)] = S(k) = \sum_{n = 0}^{2N-1}s(n)W_{2N}^{nk},\quad where\quad 0\leq k \leq 2N-1$

$S(k) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)W_{2N}^{nk}+\displaystyle\sum\limits_{n = N}^{2N-1}x(2N-n-1)W_{2N}^{nk};\quad where\quad 0\leq k\leq 2N-1$

$\Rightarrow S(k) = W_{2N}^{-k/2}+\sum_{n = 0}^{N-1}x(n) [W_{2N}^{nk}W_{2N}^{k/2}+W_{2N}^{-nk}W_{2N}^{-k/2}];\quad where\quad 0\leq k\leq 2N-1$

$\Rightarrow S(k) = W_{2N}^{\frac{k}{2}}\sum_{n = 0}^{N-1}x(n)\cos [\frac{\pi}{N}(n+\frac{1}{2})k];\quad where\quad 0\leq k\leq 2N-1$

DCT ถูกกำหนดโดย

$V(k) = 2\sum_{n = 0}^{N-1}x(n)\cos [\frac{\pi}{2}(n+\frac{1}{2})k]\quad where\quad 0\leq k\leq N-1$

$\Rightarrow V(k) = W_{2N}^{\frac{k}{2}}S(k)\quad or\quad S(k) = W_{2N}^{\frac{k}{2}}V(k),\quad where\quad 0\leq k\leq N-1$

$\Rightarrow V(k) = 2R[W_{2N}^{\frac{k}{2}}\sum_{n = 0}^{N-1}x(n)W_{2N}^{nk}],\quad where\quad 0\leq k\leq N-1$

ตัวอย่าง 1

ตรวจสอบทฤษฎีบทของลำดับของ Parseval $x(n) = \frac{1^n}{4}u(n)$

Solution - $\displaystyle\sum\limits_{-\infty}^\infty|x_1(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X_1(e^{j\omega})|^2d\omega$

LHS $\displaystyle\sum\limits_{-\infty}^\infty|x_1(n)|^2$

$= \displaystyle\sum\limits_{-\infty}^{\infty}x(n)x^*(n)$

$= \displaystyle\sum\limits_{-\infty}^\infty(\frac{1}{4})^{2n}u(n) = \frac{1}{1-\frac{1}{16}} = \frac{16}{15}$

RHS $X(e^{j\omega}) = \frac{1}{1-\frac{1}{4}e-j\omega} = \frac{1}{1-0.25\cos \omega+j0.25\sin \omega}$

$\Longleftrightarrow X^*(e^{j\omega}) = \frac{1}{1-0.25\cos \omega-j0.25\sin \omega}$

การคำนวณ $X(e^{j\omega}).X^*(e^{j\omega})$

$= \frac{1}{(1-0.25\cos \omega)^2+(0.25\sin \omega)^2} = \frac{1}{1.0625-0.5\cos \omega}$

$\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{1}{1.0625-0.5\cos \omega}d\omega$

$\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{1}{1.0625-0.5\cos \omega}d\omega = 16/15$

เราจะเห็นว่า LHS = RHS (จึงพิสูจน์แล้ว)

ตัวอย่าง 2

คำนวณ N-point DFT ของ $x(n) = 3\delta (n)$

Solution - เรารู้ว่า

$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{\frac{j2\Pi kn}{N}}$

$= \displaystyle\sum\limits_{n = 0}^{N-1}3\delta(n)e^{\frac{j2\Pi kn}{N}}$

$ = 3\delta (0)\times e^0 = 1$

ดังนั้น,$x(k) = 3,0\leq k\leq N-1$…ตอบ

ตัวอย่างที่ 3

คำนวณ N-point DFT ของ $x(n) = 7(n-n_0)$

Solution - เรารู้ว่า

$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{\frac{j2\Pi kn}{N}}$

แทนที่ค่าของ x (n)

$\displaystyle\sum\limits_{n = 0}^{N-1}7\delta (n-n_0)e^{-\frac{j2\Pi kn}{N}}$

$= e^{-kj14\Pi kn_0/N}$…ตอบ

ในวิธีการ DFT ก่อนหน้านี้เราพบว่าส่วนการคำนวณยาวเกินไป เราต้องการลดสิ่งนั้น ซึ่งสามารถทำได้ผ่าน FFT หรือการแปลงฟูเรียร์อย่างรวดเร็ว ดังนั้นเราสามารถพูดได้ว่า FFT ไม่ใช่อะไรนอกจากการคำนวณการแปลงฟูริเยร์แบบไม่ต่อเนื่องในรูปแบบอัลกอริทึมซึ่งส่วนการคำนวณจะลดลง

ข้อได้เปรียบหลักของการมี FFT คือเราสามารถออกแบบฟิลเตอร์ FIR ได้ด้วยวิธีนี้ ในทางคณิตศาสตร์ FFT สามารถเขียนได้ดังนี้

$$x[K] = \displaystyle\sum\limits_{n = 0}^{N-1}x[n]W_N^{nk}$$

ให้เรานำตัวอย่างเพื่อทำความเข้าใจให้ดีขึ้น เราได้พิจารณาแปดจุดที่ตั้งชื่อจาก$x_0\quad to\quad x_7$. เราจะเลือกคำที่เป็นคู่ในกลุ่มหนึ่งและคำที่แปลกในอีกกลุ่มหนึ่ง มุมมองแผนภาพดังกล่าวข้างต้นได้แสดงไว้ด้านล่าง -

ที่นี่คะแนน x ₀ , x ₂ , x ₄และ x ₆ถูกจัดกลุ่มเป็นหมวดหมู่เดียวและในทำนองเดียวกันคะแนน x ₁ , x ₃ , x ₅และ x ₇ถูกจัดอยู่ในหมวดหมู่อื่น ตอนนี้เราสามารถทำให้มันเป็นกลุ่มสองกลุ่มและสามารถดำเนินการคำนวณต่อไปได้ ตอนนี้ให้เราดูว่าการแบ่งออกเป็นสองส่วนเพิ่มเติมช่วยในการคำนวณอย่างไร

$x[k] = \displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r]W_N^{2rk}+\displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_N^{(2r+1)k}$

$= \sum_{r = 0}^{\frac{N}{2}-1}x[2r]W_{N/2}^{rk}+\sum_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_{N/2}^{rk}\times W_N^k$

$= G[k]+H[k]\times W_N^k$

เริ่มแรกเราใช้ลำดับแปดจุด แต่ต่อมาเราแบ่งส่วนนั้นออกเป็นสองส่วน G [k] และ H [k] G [k] ย่อมาจากส่วนคู่ในขณะที่ H [k] ย่อมาจากส่วนคี่ หากเราต้องการทราบผ่านแผนภาพก็สามารถแสดงได้ดังต่อไปนี้ -

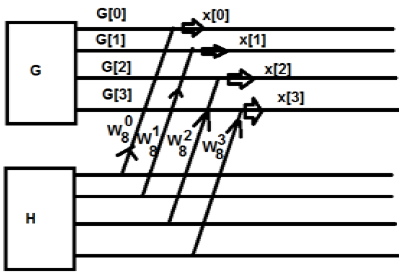
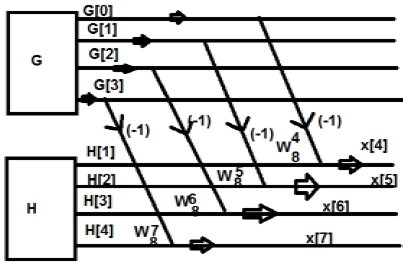
จากรูปด้านบนเราจะเห็นว่า

$W_8^4 = -1$

$W_8^5 = -W_8^1$

$W_8^6 = -W_8^2$

$W_8^7 = -W_8^3$

ในทำนองเดียวกันค่าสุดท้ายสามารถเขียนได้ดังนี้ -

$G[0]-H[0] = x[4]$

$G[1]-W_8^1H[1] = x[5]$

$G[2]-W_8^2H[2] = x[6]$

$G[1]-W_8^3H[3] = x[7]$

หนึ่งข้างต้นเป็นอนุกรมเป็นระยะ ข้อเสียของระบบนี้คือ K ไม่สามารถหักเกิน 4 จุดได้ ตอนนี้ให้เราแบ่งข้างต้นเป็นเพิ่มเติม เราจะได้โครงสร้างประมาณนี้

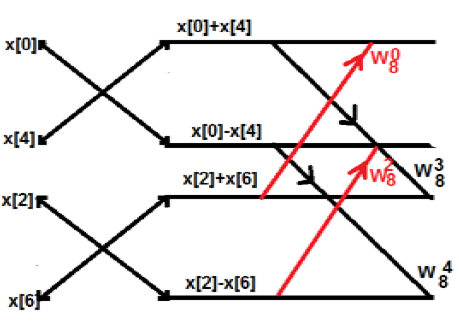
ตัวอย่าง

พิจารณาลำดับ x [n] = {2,1, -1, -3,0,1,2,1} คำนวณ FFT

Solution - ลำดับที่กำหนดคือ x [n] = {2,1, -1, -3,0,1,2,1}

จัดเรียงเงื่อนไขตามที่แสดงด้านล่าง

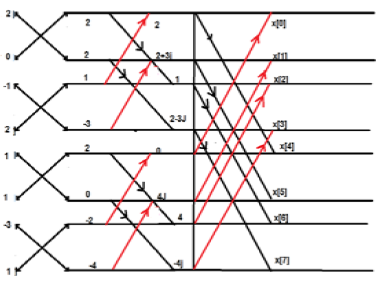
การใช้หน่วยความจำอย่างมีประสิทธิภาพนี้เป็นสิ่งสำคัญสำหรับการออกแบบฮาร์ดแวร์ที่รวดเร็วเพื่อคำนวณ FFT คำว่าการคำนวณแบบแทนที่ใช้เพื่ออธิบายการใช้หน่วยความจำนี้

การลดลงตามลำดับเวลา

ในโครงสร้างนี้เราแสดงจุดทั้งหมดในรูปแบบไบนารีเช่นใน 0 และ 1 จากนั้นเราจะย้อนกลับโครงสร้างเหล่านั้น ลำดับที่เราได้รับหลังจากนั้นเรียกว่าลำดับการกลับรายการบิต สิ่งนี้เรียกอีกอย่างว่าการสลายตัวตามลำดับเวลา การคำนวณแบบแทนที่ของ DFT แปดจุดจะแสดงในรูปแบบตารางดังที่แสดงด้านล่าง -

คะแนน	รูปแบบไบนารี	REVERSAL	คะแนนเทียบเท่า
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7

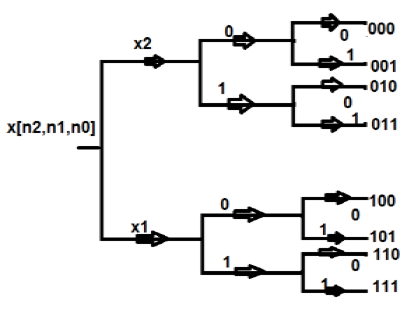
การลดลงในลำดับความถี่

นอกเหนือจากลำดับเวลาแล้วยังสามารถแสดงลำดับจุด N เป็นความถี่ได้อีกด้วย ให้เราใช้ลำดับสี่จุดเพื่อทำความเข้าใจให้ดีขึ้น

ให้ลำดับเป็น $x[0], x[1], x[2], x[3], x[4], x[5], x[6], x[7]$. เราจะจับกลุ่มสองจุดเป็นกลุ่มเดียวในตอนแรก ในทางคณิตศาสตร์ลำดับนี้สามารถเขียนเป็น;

$$x[k] = \sum_{n = 0}^{N-1}x[n]W_N^{n-k}$$

ตอนนี้ให้เราสร้างกลุ่มของลำดับหมายเลข 0 ถึง 3 กลุ่มหนึ่งและอีกกลุ่มของลำดับที่ 4 ถึง 7 ตอนนี้ในทางคณิตศาสตร์สามารถแสดงเป็น;

$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[n]W_N^{nk}+\displaystyle\sum\limits_{n = N/2}^{N-1}x[n]W_N^{nk}$$

ให้เราแทนที่ n ด้วย r โดยที่ r = 0, 1, 2 …. (N / 2-1) ในทางคณิตศาสตร์

$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[r]W_{N/2}^{nr}$$

เราใช้สี่จุดแรก (x [0], x [1], x [2], x [3]) ในตอนแรกและพยายามแทนค่าทางคณิตศาสตร์ดังนี้ -

$\sum_{n = 0}^3x[n]W_8^{nk}+\sum_{n = 0}^3x[n+4]W_8^{(n+4)k}$

$= \lbrace \sum_{n = 0}^3x[n]+\sum_{n = 0}^3x[n+4]W_8^{(4)k}\rbrace \times W_8^{nk}$

ตอนนี้ $X[0] = \sum_{n = 0}^3(X[n]+X[n+4])$

$X[1] = \sum_{n = 0}^3(X[n]+X[n+4])W_8^{nk}$

$= [X[0]-X[4]+(X[1]-X[5])W_8^1+(X[2]-X[6])W_8^2+(X[3]-X[7])W_8^3$

เราสามารถแบ่งมันออกเป็นสองส่วนได้อีกซึ่งหมายความว่าแทนที่จะแบ่งเป็นลำดับ 4 จุดเราสามารถแบ่งมันออกเป็นลำดับ 2 จุดได้

ฟิลเตอร์ FIR มีประโยชน์ในการออกแบบฟิลเตอร์โดยใช้คอมพิวเตอร์ช่วย ให้เราดูตัวอย่างและดูว่ามันทำงานอย่างไร ให้ด้านล่างเป็นรูปของตัวกรองที่ต้องการ

ในขณะที่ทำการออกแบบคอมพิวเตอร์เราแบ่งตัวเลขกราฟต่อเนื่องทั้งหมดออกเป็นค่าที่ไม่ต่อเนื่อง ภายในขอบเขตที่กำหนดเราแบ่งออกเป็น 64, 256 หรือ 512 (และอื่น ๆ ) จำนวนชิ้นส่วนที่มีขนาดไม่ต่อเนื่อง

ในตัวอย่างข้างต้นเราได้กำหนดขีด จำกัด ระหว่าง-πถึง + π เราได้แบ่งออกเป็น 256 ส่วน จุดสามารถแสดงเป็น H (0), H (1), …. สูงถึง H (256) ที่นี่เราใช้อัลกอริทึม IDFT และสิ่งนี้จะทำให้เรามีลักษณะเฟสเชิงเส้น

บางครั้งเราอาจสนใจลำดับตัวกรองบางอย่าง ขอให้เราบอกว่าเราต้องการที่จะตระหนักถึงข้างต้นการออกแบบได้รับถึง 9 ^THกรองการสั่งซื้อ ดังนั้นเราจึงใช้ค่าตัวกรองเป็น h0, h1, h2 … .h9 ในทางคณิตศาสตร์แสดงได้ดังต่อไปนี้

$$H(e^{j\omega}) = h_0+h_1e^{-j\omega}+h_2e^{-2j\omega}+.....+h_9e^{-9j\omega}$$

ในกรณีที่มีความคลาดเคลื่อนจำนวนมากเราจะได้คะแนนสูงสุด

ตัวอย่างเช่นในรูปด้านบนมีการลดลงอย่างกะทันหันระหว่างจุด B และ C ดังนั้นเราจึงพยายามหาค่าที่ไม่ต่อเนื่องมากขึ้น ณ จุดนี้ แต่มีความชันคงที่ระหว่างจุด C และ D ที่นั่นเราใช้เวลา จำนวนค่าที่ไม่ต่อเนื่องน้อยลง

สำหรับการออกแบบตัวกรองด้านบนเราต้องผ่านขั้นตอนการย่อขนาดดังนี้

$H(e^{j\omega1}) = h_0+h_1e^{-j\omega1}+h_2e^{-2j\omega1}+.....+h_9e^{-9j\omega1}$

$H(e^{j\omega2}) = h_0+h_1e^{-j\omega2}+h_2e^{-2j\omega2}+.....+h_9e^{-9j\omega2}$

ในทำนองเดียวกัน

$(e^{j\omega1000}) = h_0+h_1eH^{-j\omega1000}h_2e^{-2j\omega1000}+.....+h_9+e^{-9j\omega1000}$

แทนสมการข้างต้นในรูปแบบเมทริกซ์เรามี -

$$\begin{bmatrix}H(e^{j\omega_1})\\.\\.\\H(e^{j\omega_{1000}}) \end{bmatrix} = \begin{bmatrix}e^{-j\omega_1} & ... & e^{-j9\omega_1} \\. & & . \\. & & . \\e^{-j\omega_{1000}} &... & e^{j9\omega_{1000}} \end{bmatrix}\begin{bmatrix}h_0\\.\\.\\h_9\end{bmatrix}$$

ให้เราใช้เมทริกซ์ 1000 × 1 เป็นเมทริกซ์ B, 1000 × 9 เป็นเมทริกซ์ A และ 9 × 1 เป็น $\hat{h}$.

ดังนั้นสำหรับการแก้เมทริกซ์ข้างต้นเราจะเขียน

$\hat{h} = [A^TA]^{-1}A^{T}B$

$= [A^{*T}A]^{-1}A^{*T}B$

โดยที่ A ^*แสดงถึงคอนจูเกตที่ซับซ้อนของเมทริกซ์ A

คะแนน	รูปแบบไบนารี	REVERSAL	คะแนนเทียบเท่า
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7

คะแนน	รูปแบบไบนารี	REVERSAL	คะแนนเทียบเท่า
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7

คะแนน	รูปแบบไบนารี	REVERSAL	คะแนนเทียบเท่า
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7