DSP - การดำเนินการเกี่ยวกับความแตกต่างของสัญญาณ

การดำเนินการที่สำคัญสองอย่างที่ดำเนินการกับสัญญาณคือการสร้างความแตกต่างและการรวม

ความแตกต่าง

ความแตกต่างของสัญญาณใด ๆ x (t) หมายถึงการแสดงความชันของสัญญาณนั้นตามเวลา ในทางคณิตศาสตร์จะแสดงเป็น;

$$ x (t) \ rightarrow \ frac {dx (t)} {dt} $$

ในกรณีของการสร้างความแตกต่างของ OPAMP วิธีการนี้มีประโยชน์มาก เราสามารถแยกความแตกต่างของสัญญาณในรูปแบบกราฟิกได้อย่างง่ายดายแทนที่จะใช้สูตร อย่างไรก็ตามเงื่อนไขคือสัญญาณต้องเป็นแบบสี่เหลี่ยมหรือสามเหลี่ยมซึ่งส่วนใหญ่จะเกิดขึ้น

สัญญาณดั้งเดิม	สัญญาณที่แตกต่าง
ทางลาด	ขั้นตอน
ขั้นตอน	แรงกระตุ้น
แรงกระตุ้น	1

ตารางด้านบนแสดงให้เห็นถึงสภาพของสัญญาณหลังจากที่มีความแตกต่าง ตัวอย่างเช่นสัญญาณทางลาดจะแปลงเป็นสัญญาณขั้นตอนหลังจากการแยกความแตกต่าง ในทำนองเดียวกันสัญญาณขั้นตอนของหน่วยจะกลายเป็นสัญญาณอิมพัลส์

ตัวอย่าง

ให้สัญญาณที่กำหนดให้เราเป็น $ x (t) = 4 [r (t) -r (t-2)] $ เมื่อมีการลงจุดสัญญาณนี้จะมีลักษณะเหมือนสัญญาณทางด้านซ้ายของรูปด้านล่าง ตอนนี้เป้าหมายของเราคือการแยกแยะสัญญาณที่กำหนด

เริ่มต้นด้วยเราจะเริ่มแยกความแตกต่างของสมการที่กำหนด เรารู้ว่าสัญญาณทางลาดหลังจากการแยกความแตกต่างให้สัญญาณขั้นตอนของหน่วย

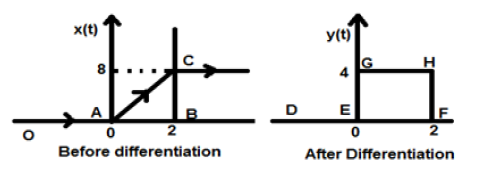
ดังนั้นสัญญาณผลลัพธ์ของเรา y (t) สามารถเขียนเป็น;

$ y (t) = \ frac {dx (t)} {dt} $

$ = \ frac {d4 [r (t) -r (t-2)]} {dt} $

$ = 4 [u (t) -u (t-2)] $

ตอนนี้สัญญาณนี้ถูกพล็อตในที่สุดซึ่งแสดงไว้ที่ด้านขวามือของรูปด้านบน