DSP - การจำแนกสัญญาณ CT
สัญญาณเวลาต่อเนื่องสามารถจำแนกได้ตามเงื่อนไขหรือการดำเนินการที่แตกต่างกันของสัญญาณ
สัญญาณคู่และคี่
แม้แต่สัญญาณ
สัญญาณบอกว่าเป็นไปตามเงื่อนไขต่อไปนี้
$$ x (-t) = x (t) $$การย้อนเวลาของสัญญาณไม่ได้หมายความถึงการเปลี่ยนแปลงใด ๆ ของแอมพลิจูดที่นี่ ตัวอย่างเช่นพิจารณาคลื่นสามเหลี่ยมที่แสดงด้านล่าง
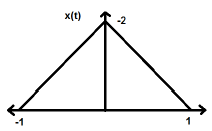
สัญญาณสามเหลี่ยมคือสัญญาณคู่ เนื่องจากแกน Y มีความสมมาตร เราสามารถพูดได้ว่าเป็นภาพสะท้อนเกี่ยวกับแกน Y
พิจารณาสัญญาณอื่นดังแสดงในรูปด้านล่าง
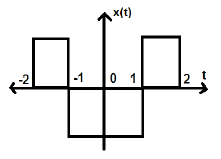
เราจะเห็นว่าสัญญาณข้างบนนั้นมีความสมมาตรเกี่ยวกับแกน Y
สัญญาณแปลก
สัญญาณจะบอกว่าเป็นเลขคี่หากเป็นไปตามเงื่อนไขต่อไปนี้
$$ x (-t) = -x (t) $$ที่นี่ทั้งการย้อนเวลาและการเปลี่ยนแปลงแอมพลิจูดจะเกิดขึ้นพร้อมกัน
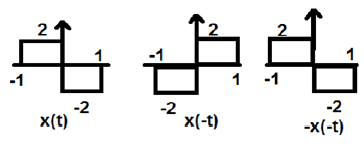
ในรูปด้านบนเราจะเห็นสัญญาณขั้นตอน x (t) ในการทดสอบว่าเป็นสัญญาณคี่หรือไม่อันดับแรกเราทำการย้อนเวลาเช่น x (-t) และผลลัพธ์จะเป็นดังที่แสดงในรูป จากนั้นเรากลับแอมพลิจูดของสัญญาณผลลัพธ์คือ –x (-t) และเราจะได้ผลลัพธ์ดังแสดงในรูป
ถ้าเราเปรียบเทียบรูปคลื่นแรกและรูปที่สามเราจะเห็นว่ามันเหมือนกันนั่นคือ x (t) = -x (-t) ซึ่งตรงตามเกณฑ์ของเรา ดังนั้นสัญญาณข้างต้นจึงเป็นสัญญาณคี่
ผลลัพธ์ที่สำคัญบางประการที่เกี่ยวข้องกับสัญญาณคู่และคี่มีให้ด้านล่าง
- Even × Even = คู่
- คี่×คี่ = คู่
- Even × Odd = คี่
- Even ± Even = Even
- คี่±คี่ = คี่
- Even ± Odd = ทั้งคู่หรือคี่
การแสดงสัญญาณใด ๆ ในรูปแบบคู่หรือคี่
สัญญาณบางอย่างไม่สามารถจำแนกเป็นประเภทคู่หรือคี่ได้โดยตรง สิ่งเหล่านี้แสดงเป็นการรวมกันของทั้งสัญญาณคู่และคี่
$$ x (t) \ rightarrow x_ {e} (t) + x_ {0} (t) $$โดยที่ x e (t) แทนสัญญาณคู่และ x o (t) แทนสัญญาณคี่
$$ x_ {e} (t) = \ frac {[x (t) + x (-t)]} {2} $$และ
$$ x_ {0} (t) = \ frac {[x (t) -x (-t)]} {2} $$ตัวอย่าง
ค้นหาส่วนคู่และคี่ของสัญญาณ $ x (n) = t + t ^ {2} + t ^ {3} $
Solution - จากการย้อนกลับ x (n) เราจะได้
$$ x (-n) = -t + t ^ {2} -t ^ {3} $$
ตอนนี้ตามสูตรส่วนคู่
$$ x_ {e} (t) = \ frac {x (t) + x (-t)} {2} $$
$$ = \ frac {[(t + t ^ {2} + t ^ {3}) + (- t + t ^ {2} -t ^ {3})]} {2} $$
$$ = t ^ {2} $$
ในทำนองเดียวกันตามสูตรส่วนที่แปลกคือ
$$ x_ {0} (t) = \ frac {[x (t) -x (-t)]} {2} $$
$$ = \ frac {[(t + t ^ {2} + t ^ {3}) - (- t + t ^ {2} -t ^ {3})]} {2} $$
$$ = t + t ^ {3} $$
สัญญาณเป็นระยะและไม่เป็นระยะ
สัญญาณเป็นระยะ
สัญญาณเป็นระยะจะทำซ้ำตัวเองหลังจากช่วงเวลาหนึ่ง เราสามารถแสดงสิ่งนี้ในรูปสมการเป็น -
$$ x (t) = x (t) \ pm nT $$โดยที่ n = จำนวนเต็ม (1,2,3 ……)
T = ช่วงเวลาพื้นฐาน (FTP) ≠ 0 และ≠∞
ช่วงเวลาพื้นฐาน (FTP) เป็นค่าบวกและค่าคงที่ที่เล็กที่สุดของเวลาที่สัญญาณเป็นระยะ
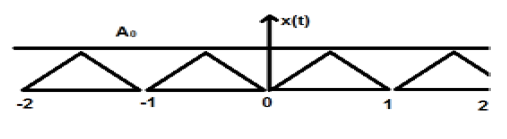
สัญญาณสามเหลี่ยมแสดงในรูปด้านบนของแอมพลิจูด A ที่นี่สัญญาณจะเกิดซ้ำทุกๆ 1 วินาที ดังนั้นเราสามารถพูดได้ว่าสัญญาณเป็นระยะและ FTP คือ 1 วินาที
สัญญาณที่ไม่เป็นระยะ
เราสามารถพูดได้ง่ายๆว่าสัญญาณที่ไม่เป็นระยะนั้นไม่ได้เกิดขึ้นเป็นระยะ เห็นได้ชัดว่าสัญญาณเหล่านี้จะไม่เกิดซ้ำหลังจากช่วงเวลาใด ๆ
สัญญาณที่ไม่เป็นระยะไม่เป็นไปตามรูปแบบที่แน่นอน ดังนั้นจึงไม่มีสมการทางคณิตศาสตร์ใดที่สามารถอธิบายสมการทางคณิตศาสตร์ได้
สัญญาณพลังงานและพลังงาน
สัญญาณกล่าวว่าเป็นสัญญาณพลังงานหากและเฉพาะในกรณีที่พลังงานทั้งหมดที่มีอยู่นั้น จำกัด และไม่ใช่ศูนย์ (0 <E <∞) ดังนั้นสำหรับสัญญาณประเภทพลังงานใด ๆ สัญญาณปกติทั้งหมดจะ จำกัด และไม่เป็นศูนย์
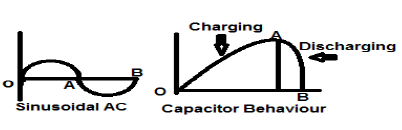
สัญญาณกระแสไฟฟ้ากระแสสลับไซน์เป็นตัวอย่างที่สมบูรณ์แบบของสัญญาณประเภทพลังงานเนื่องจากอยู่ในครึ่งรอบที่เป็นบวกในกรณีหนึ่งจากนั้นเป็นค่าลบในครึ่งรอบถัดไป ดังนั้นกำลังเฉลี่ยจึงกลายเป็นศูนย์
ตัวเก็บประจุแบบไม่สูญเสียเป็นตัวอย่างที่สมบูรณ์แบบของสัญญาณประเภทพลังงานเนื่องจากเมื่อเชื่อมต่อกับแหล่งที่มามันจะชาร์จได้ถึงระดับที่เหมาะสมและเมื่อถอดแหล่งที่มาตัวเก็บประจุจะกระจายพลังงานในปริมาณที่เท่ากันผ่านโหลดและทำให้พลังงานเฉลี่ยเป็น ศูนย์.
สำหรับสัญญาณ จำกัด ใด ๆ x (t) พลังงานสามารถเป็นสัญลักษณ์เป็น E และเขียนเป็น;
$$ E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt $$ความหนาแน่นของสเปกตรัมของสัญญาณประเภทพลังงานให้ปริมาณพลังงานที่กระจายในระดับความถี่ต่างๆ
สัญญาณประเภทพลังงาน
สัญญาณกล่าวว่าเป็นสัญญาณประเภทพลังงานถ้าและเฉพาะในกรณีที่กำลังเฉลี่ยปกติจะ จำกัด และไม่ใช่ศูนย์เช่น (0 <p <∞) สำหรับสัญญาณประเภทพลังงานกำลังเฉลี่ยปกติจะ จำกัด และไม่เป็นศูนย์ สัญญาณประจำงวดเกือบทั้งหมดเป็นสัญญาณกำลังและกำลังเฉลี่ยของพวกมันนั้น จำกัด และไม่เป็นศูนย์
ในรูปแบบทางคณิตศาสตร์พลังของสัญญาณ x (t) สามารถเขียนเป็น;
$$ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt $$ความแตกต่างระหว่างสัญญาณพลังงานและพลังงาน
ตารางต่อไปนี้สรุปความแตกต่างของสัญญาณพลังงานและพลังงาน
| สัญญาณไฟ | สัญญาณพลังงาน |
|---|---|
| สัญญาณระยะปฏิบัติเป็นสัญญาณกำลัง | สัญญาณที่ไม่เป็นระยะคือสัญญาณพลังงาน |
| ที่นี่กำลังเฉลี่ยปกตินั้น จำกัด และไม่ใช่ศูนย์ | ที่นี่พลังงานที่ปรับมาตรฐานทั้งหมดมีค่า จำกัด และไม่เป็นศูนย์ |
| ในทางคณิตศาสตร์ $$ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt $$ |
ในทางคณิตศาสตร์ $$ E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt $$ |
| การมีอยู่ของสัญญาณเหล่านี้ไม่มีที่สิ้นสุดเมื่อเวลาผ่านไป | สัญญาณเหล่านี้มีอยู่ในช่วงเวลา จำกัด |
| พลังงานของสัญญาณกำลังไม่มีที่สิ้นสุดในช่วงเวลาที่ไม่มีที่สิ้นสุด | พลังของสัญญาณพลังงานเป็นศูนย์ในช่วงเวลาที่ไม่มีที่สิ้นสุด |
ตัวอย่างที่แก้ไข
Example 1 - ค้นหาพลังของสัญญาณ $ z (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) + 4 \ sin (3 \ Pi + 30 ^ {o}) $
Solution- สัญญาณสองสัญญาณข้างต้นมีมุมฉากซึ่งกันและกันเนื่องจากเงื่อนไขความถี่เหมือนกันและมีความแตกต่างของเฟสเดียวกัน ดังนั้นพลังทั้งหมดจะเป็นการรวมพลังของแต่ละบุคคล
ให้ $ z (t) = x (t) + y (t) $
โดยที่ $ x (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) $ และ $ y (t) = 4 \ sin (3 \ Pi + 30 ^ {o}) $
พลังของ $ x (t) = \ frac {2 ^ {2}} {2} = 2 $
พลังของ $ y (t) = \ frac {4 ^ {2}} {2} = 8 $
ดังนั้น$ P (z) = p (x) + p (y) = 2 + 8 = 10 $ ... Ans.
Example 2 - ทดสอบว่าสัญญาณที่ให้ $ x (t) = t ^ {2} + j \ sin t $ เป็นคอนจูเกตหรือไม่?
Solution- ตรงนี้ส่วนที่แท้จริงของ t 2คือส่วนที่เป็นคู่และส่วนที่แปลก (จินตภาพ) เป็น $ \ sin t $ เป็นเลขคี่ สัญญาณข้างต้นจึงเป็นสัญญาณ Conjugate
Example 3 - ตรวจสอบว่า $ X (t) = \ sin \ omega t $ เป็นสัญญาณคี่หรือสัญญาณคู่
Solution - ให้ $ X (t) = \ sin \ omega t $
เมื่อย้อนเวลาเราจะได้ $ \ sin (- \ omega t) $
แต่เรารู้ว่า $ \ sin (- \ phi) = - \ sin \ phi $.
ดังนั้น,
$$ \ sin (- \ omega t) = - \ sin \ omega t $$นี่เป็นเงื่อนไขที่ทำให้สัญญาณเป็นคี่ ดังนั้น $ \ sin \ omega t $ จึงเป็นสัญญาณแปลก ๆ