DSP - การแปลงฟูริเยร์อย่างรวดเร็ว
ในวิธีการ DFT ก่อนหน้านี้เราพบว่าส่วนการคำนวณยาวเกินไป เราต้องการลดสิ่งนั้น ซึ่งสามารถทำได้ผ่าน FFT หรือการแปลงฟูเรียร์อย่างรวดเร็ว ดังนั้นเราสามารถพูดได้ว่า FFT ไม่ใช่อะไรนอกจากการคำนวณการแปลงฟูริเยร์แบบไม่ต่อเนื่องในรูปแบบอัลกอริทึมซึ่งส่วนการคำนวณจะลดลง
ข้อได้เปรียบหลักของการมี FFT คือเราสามารถออกแบบฟิลเตอร์ FIR ได้ด้วยวิธีนี้ ในทางคณิตศาสตร์ FFT สามารถเขียนได้ดังนี้
$$ x [K] = \ displaystyle \ sum \ LIMIT_ {n = 0} ^ {N-1} x [n] W_N ^ {nk} $$ให้เรานำตัวอย่างเพื่อทำความเข้าใจให้ดีขึ้น เราได้พิจารณาแปดจุดที่ตั้งชื่อจาก $ x_0 \ quad ถึง \ quad x_7 $ เราจะเลือกคำที่เป็นคู่ในกลุ่มหนึ่งและคำที่แปลกในอีกกลุ่มหนึ่ง มุมมองแผนภาพดังกล่าวข้างต้นได้แสดงไว้ด้านล่าง -
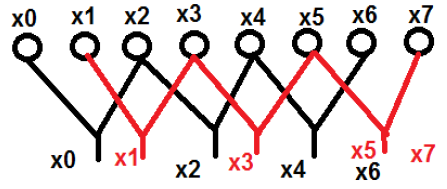
ที่นี่คะแนน x 0 , x 2 , x 4และ x 6ถูกจัดกลุ่มเป็นหมวดหมู่เดียวและในทำนองเดียวกันคะแนน x 1 , x 3 , x 5และ x 7ถูกจัดอยู่ในหมวดหมู่อื่น ตอนนี้เราสามารถทำให้มันอยู่ในกลุ่มสองกลุ่มและดำเนินการคำนวณต่อไปได้ ตอนนี้ให้เราดูว่าการแบ่งออกเป็นสองส่วนเพิ่มเติมช่วยในการคำนวณอย่างไร
$ x [k] = \ displaystyle \ sum \ LIMIT_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_N ^ {2rk} + \ displaystyle \ sum \ LIMIT_ {r = 0 } ^ {\ frac {N} {2} -1} x [2r + 1] W_N ^ {(2r + 1) k} $
$ = \ sum_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_ {N / 2} ^ {rk} + \ sum_ {r = 0} ^ {\ frac {N } {2} -1} x [2r + 1] W_ {N / 2} ^ {rk} \ times W_N ^ k $
$ = G [k] + H [k] \ times W_N ^ k $
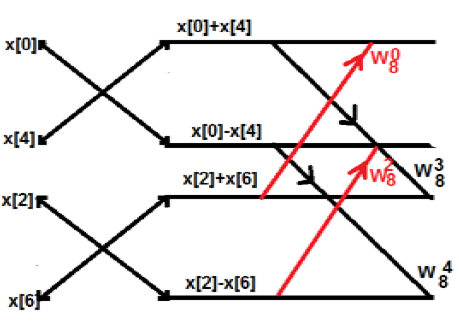
เริ่มแรกเราใช้ลำดับแปดจุด แต่ต่อมาเราแบ่งส่วนนั้นออกเป็นสองส่วน G [k] และ H [k] G [k] ย่อมาจากส่วนคู่ในขณะที่ H [k] ย่อมาจากส่วนคี่ หากเราต้องการทราบผ่านแผนภาพก็สามารถแสดงได้ดังต่อไปนี้ -
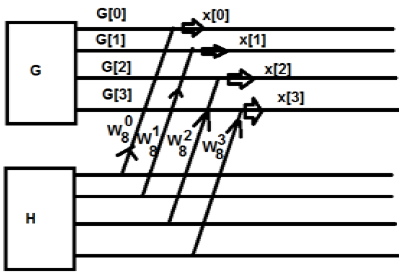
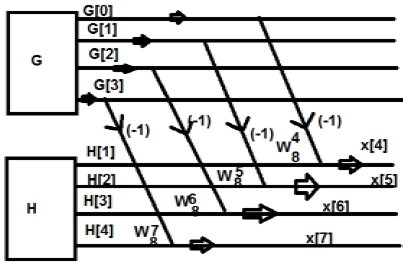
จากรูปด้านบนเราจะเห็นว่า
$ W_8 ^ 4 = -1 $
$ W_8 ^ 5 = -W_8 ^ 1 $
$ W_8 ^ 6 = -W_8 ^ 2 $
$ W_8 ^ 7 = -W_8 ^ 3 $
ในทำนองเดียวกันค่าสุดท้ายสามารถเขียนได้ดังนี้ -
$ G [0] -H [0] = x [4] $
$ G [1] -W_8 ^ 1H [1] = x [5] $
$ G [2] -W_8 ^ 2H [2] = x [6] $
$ G [1] -W_8 ^ 3H [3] = x [7] $
ด้านบนเป็นซีรีส์เป็นระยะ ข้อเสียของระบบนี้คือ K ไม่สามารถหักเกิน 4 จุดได้ ตอนนี้ให้เราแบ่งข้างต้นเป็นเพิ่มเติม เราจะได้โครงสร้างประมาณนี้
ตัวอย่าง
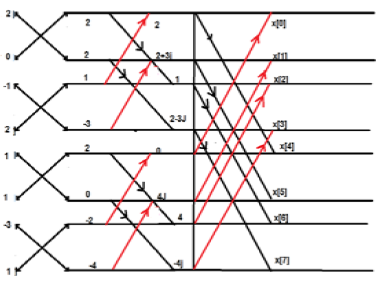
พิจารณาลำดับ x [n] = {2,1, -1, -3,0,1,2,1} คำนวณ FFT
Solution - ลำดับที่กำหนดคือ x [n] = {2,1, -1, -3,0,1,2,1}
จัดเรียงเงื่อนไขตามที่แสดงด้านล่าง