DSP - การคำนวณในสถานที่
การใช้หน่วยความจำอย่างมีประสิทธิภาพนี้เป็นสิ่งสำคัญสำหรับการออกแบบฮาร์ดแวร์ที่รวดเร็วเพื่อคำนวณ FFT คำว่าการคำนวณแบบแทนที่ใช้เพื่ออธิบายการใช้หน่วยความจำนี้
การลดลงตามลำดับเวลา
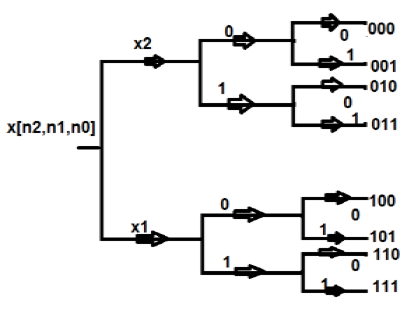
ในโครงสร้างนี้เราแสดงจุดทั้งหมดในรูปแบบไบนารีเช่นใน 0 และ 1 จากนั้นเราจะย้อนกลับโครงสร้างเหล่านั้น ลำดับที่เราได้รับหลังจากนั้นเรียกว่าลำดับการกลับรายการบิต สิ่งนี้เรียกอีกอย่างว่าการสลายตัวตามลำดับเวลา การคำนวณแบบแทนที่ของ DFT แปดจุดจะแสดงในรูปแบบตารางดังที่แสดงด้านล่าง -
| คะแนน | รูปแบบไบนารี | REVERSAL | คะแนนเทียบเท่า |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
การลดลงในลำดับความถี่
นอกเหนือจากลำดับเวลาแล้วยังสามารถแสดงลำดับจุด N เป็นความถี่ได้อีกด้วย ให้เราใช้ลำดับสี่จุดเพื่อทำความเข้าใจให้ดีขึ้น
ให้ลำดับเป็น $ x [0], x [1], x [2], x [3], x [4], x [5], x [6], x [7] $ เราจะจับกลุ่มสองจุดเป็นกลุ่มเดียวในตอนแรก ในทางคณิตศาสตร์ลำดับนี้สามารถเขียนเป็น;
$$ x [k] = \ sum_ {n = 0} ^ {N-1} x [n] W_N ^ {nk} $$ตอนนี้ให้เราสร้างกลุ่มของลำดับหมายเลข 0 ถึง 3 กลุ่มหนึ่งและอีกกลุ่มของลำดับที่ 4 ถึง 7 ตอนนี้ในทางคณิตศาสตร์สามารถแสดงได้ดังนี้
$$ \ displaystyle \ sum \ LIMIT_ {n = 0} ^ {\ frac {N} {2} -1} x [n] W_N ^ {nk} + \ displaystyle \ sum \ LIMIT_ {n = N / 2} ^ {N-1} x [n] W_N ^ {nk} $$ให้เราแทนที่ n ด้วย r โดยที่ r = 0, 1, 2 …. (N / 2-1) ในทางคณิตศาสตร์
$$ \ displaystyle \ sum \ LIMIT_ {n = 0} ^ {\ frac {N} {2} -1} x [r] W_ {N / 2} ^ {nr} $$เรานำสี่จุดแรก (x [0], x [1], x [2], x [3]) ในตอนแรกและพยายามแทนค่าทางคณิตศาสตร์ดังนี้ -
$ \ sum_ {n = 0} ^ 3x [n] W_8 ^ {nk} + \ sum_ {n = 0} ^ 3x [n + 4] W_8 ^ {(n + 4) k} $
$ = \ lbrace \ sum_ {n = 0} ^ 3x [n] + \ sum_ {n = 0} ^ 3x [n + 4] W_8 ^ {(4) k} \ rbrace \ times W_8 ^ {nk} $
ตอนนี้$ X [0] = \ sum_ {n = 0} ^ 3 (X [n] + X [n + 4]) $
$ X [1] = \ sum_ {n = 0} ^ 3 (X [n] + X [n + 4]) W_8 ^ {nk} $
$ = [X [0] -X [4] + (X [1] -X [5]) W_8 ^ 1 + (X [2] -X [6]) W_8 ^ 2 + (X [3] -X [7]) W_8 ^ 3 $
เราสามารถแบ่งมันออกเป็นสองส่วนได้อีกซึ่งหมายความว่าแทนที่จะแบ่งเป็นลำดับ 4 จุดเราสามารถแบ่งมันออกเป็นลำดับ 2 จุดได้