DSP - การดำเนินการเกี่ยวกับการเปลี่ยนสัญญาณ
การขยับหมายถึงการเคลื่อนที่ของสัญญาณทั้งในโดเมนเวลา (รอบแกน Y) หรือในโดเมนแอมพลิจูด (รอบแกน X) ดังนั้นเราสามารถแบ่งประเภทของการขยับออกเป็นสองประเภทที่เรียกว่าการเปลี่ยนเวลาและการขยับแอมพลิจูดซึ่งจะกล่าวถึงต่อไปด้านล่าง
การเปลี่ยนเวลา
การเปลี่ยนเวลาหมายถึงการเปลี่ยนสัญญาณในโดเมนเวลา ในทางคณิตศาสตร์สามารถเขียนเป็น
$$ x (t) \ rightarrow y (t + k) $$ค่า K นี้อาจเป็นบวกหรืออาจเป็นลบ ตามสัญลักษณ์ของค่า k เรามีการขยับสองประเภทที่เรียกว่าการขยับขวาและการขยับซ้าย
กรณีที่ 1 (K> 0)
เมื่อ K มีค่ามากกว่าศูนย์การขยับของสัญญาณจะไปทาง "ซ้าย" ในโดเมนเวลา ดังนั้นการเปลี่ยนประเภทนี้จึงเรียกว่าการขยับซ้ายของสัญญาณ
Example
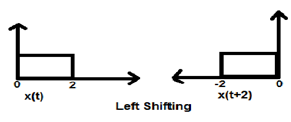
กรณีที่ 2 (K <0)
เมื่อ K น้อยกว่าศูนย์การเปลี่ยนสัญญาณจะเกิดขึ้นไปทางขวาในโดเมนเวลา ดังนั้นการเปลี่ยนประเภทนี้จึงเรียกว่าการขยับขวา
Example
รูปด้านล่างแสดงการเปลี่ยนสัญญาณอย่างถูกต้องโดย 2
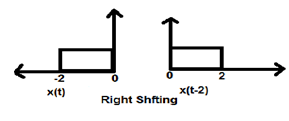
การขยับของแอมพลิจูด
การเปลี่ยนแอมพลิจูดหมายถึงการเปลี่ยนสัญญาณในโดเมนแอมพลิจูด (รอบแกน X) ในทางคณิตศาสตร์สามารถแสดงเป็น -
$$ x (t) \ rightarrow x (t) + K $$ค่า K นี้อาจเป็นบวกหรือลบ ดังนั้นเราจึงมีการเปลี่ยนแอมพลิจูดสองประเภทซึ่งจะกล่าวถึงในภายหลัง
กรณีที่ 1 (K> 0)
เมื่อ K มีค่ามากกว่าศูนย์การขยับของสัญญาณจะเกิดขึ้นในแกน x ดังนั้นการขยับประเภทนี้จึงเรียกว่าการขยับขึ้น
Example
ให้เราพิจารณาสัญญาณ x (t) ซึ่งกำหนดให้เป็น;
$$ x = \ begin {cases} 0, & t <0 \\ 1, & 0 \ leq t \ leq 2 \\ 0, & t> 0 \ end {cases} $$ให้เรานำ K = + 1 เพื่อให้สัญญาณใหม่สามารถเขียนเป็น -
$ y (t) \ rightarrow x (t) + 1 $ ดังนั้น y (t) จึงสามารถเขียนเป็น;
$$ x (t) = \ begin {cases} 1, & t <0 \\ 2, & 0 \ leq t \ leq 2 \\ 1, & t> 0 \ end {cases} $$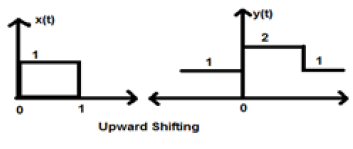
กรณีที่ 2 (K <0)
เมื่อ K น้อยกว่าศูนย์การขยับของสัญญาณจะเกิดขึ้นไปด้านล่างในแกน X- ดังนั้นจึงเรียกว่าการขยับลงของสัญญาณ
Example
ให้เราพิจารณาสัญญาณ x (t) ซึ่งกำหนดให้เป็น;
$$ x (t) = \ begin {cases} 0, & t <0 \\ 1, & 0 \ leq t \ leq 2 \\ 0, & t> 0 \ end {cases} $$ให้เรานำ K = -1 เพื่อให้สัญญาณใหม่สามารถเขียนเป็น;
$ y (t) \ rightarrow x (t) -1 $ ดังนั้น y (t) จึงสามารถเขียนเป็น;
$$ y (t) = \ begin {cases} -1, & t <0 \\ 0, & 0 \ leq t \ leq 2 \\ -1, & t> 0 \ end {cases} $$