DSP - คุณสมบัติ Z-Transform

ในบทนี้เราจะเข้าใจคุณสมบัติพื้นฐานของการแปลง Z

ความเป็นเส้นตรง

ระบุว่าเมื่อสัญญาณที่ไม่ต่อเนื่องสองสัญญาณหรือมากกว่านั้นคูณด้วยค่าคงที่การแปลง Z ตามลำดับจะถูกคูณด้วยค่าคงที่เดียวกัน

ในทางคณิตศาสตร์

$$ a_1x_1 (n) + a_2x_2 (n) = a_1X_1 (z) + a_2X_2 (z) $$

Proof - เรารู้ว่า

$$ X (Z) = \ sum_ {n = - \ infty} ^ \ infty x (n) Z ^ {- n} $$

$ = \ sum_ {n = - \ infty} ^ \ infty (a_1x_1 (n) + a_2x_2 (n)) Z ^ {- n} $

$ = a_1 \ sum_ {n = - \ infty} ^ \ infty x_1 (n) Z ^ {- n} + a_2 \ sum_ {n = - \ infty} ^ \ infty x_2 (n) Z ^ {- n} $

$ = a_1X_1 (z) + a_2X_2 (z) $ (ดังนั้นจึงพิสูจน์แล้ว)

ที่นี่ ROC คือ $ ROC_1 \ bigcap ROC_2 $

การเปลี่ยนเวลา

คุณสมบัติการเปลี่ยนเวลาแสดงให้เห็นว่าการเปลี่ยนแปลงของโดเมนเวลาในสัญญาณไม่ต่อเนื่องจะส่งผลต่อโดเมน Z ซึ่งสามารถเขียนเป็น;

$$ x (n-n_0) \ longleftrightarrow X (Z) Z ^ {- n} $$

หรือ$ x (n-1) \ longleftrightarrow Z ^ {- 1} X (Z) $

Proof -

ให้$ y (P) = X (PK) $

$ Y (z) = \ sum_ {p = - \ infty} ^ \ infty y (p) Z ^ {- p} $

$ = \ sum_ {p = - \ infty} ^ \ infty (x (pk)) Z ^ {- p} $

ให้ s = pk

$ = \ sum_ {s = - \ infty} ^ \ infty x (s) Z ^ {- (s + k)} $

$ = \ sum_ {s = - \ infty} ^ \ infty x (s) Z ^ {- s} Z ^ {- k} $

$ = Z ^ {- k} [\ sum_ {s = - \ infty} ^ \ infty x (m) Z ^ {- s}] $

$ = Z ^ {- k} X (Z) $ (ดังนั้นจึงพิสูจน์แล้ว)

ที่นี่ ROC สามารถเขียนเป็น Z = 0 (p> 0) หรือ Z = ∞ (p <0)

ตัวอย่าง

สามารถลงจุด U (n) และ U (n-1) ได้ดังนี้

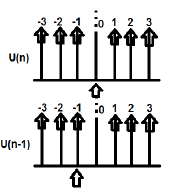
Z-transformation ของ U (n) cab เขียนเป็น;

$ \ sum_ {n = - \ infty} ^ \ infty [U (n)] Z ^ {- n} = 1 $

การแปลง Z ของ U (n-1) สามารถเขียนเป็น;

$ \ sum_ {n = - \ infty} ^ \ infty [U (n-1)] Z ^ {- n} = Z ^ {- 1} $

ที่นี่ $ x (n-n_0) = Z ^ {- n_0} X (Z) $ (จึงพิสูจน์แล้ว)

การปรับเวลา

คุณสมบัติ Time Scaling บอกเราว่าโดเมน Z ของสัญญาณจะเป็นอย่างไรเมื่อเวลาถูกปรับขนาดในรูปแบบไม่ต่อเนื่องซึ่งสามารถเขียนเป็น;

$$ a ^ nx (n) \ longleftrightarrow X (a ^ {- 1} Z) $$

Proof -

ให้$ y (p) = a ^ {p} x (p) $

$ Y (P) = \ sum_ {p = - \ infty} ^ \ infty y (p) Z ^ {- p} $

$ = \ sum_ {p = - \ infty} ^ \ infty a ^ px (p) Z ^ {- p} $

$ = \ sum_ {p = - \ infty} ^ \ infty x (p) [a ^ {- 1} Z] ^ {- p} $

$ = X (a ^ {- 1} Z) $ (จึงพิสูจน์แล้ว)

ROC: = Mod (ar1) <Mod (Z) <Mod (ar2) โดยที่ Mod = Modulus

ตัวอย่าง

ให้เราตรวจสอบการแปลง Z ของ $ x (n) = a ^ n \ cos \ omega n $ โดยใช้คุณสมบัติการปรับเวลา

Solution -

เรารู้แล้วว่าการแปลง Z ของสัญญาณ $ \ cos (\ omega n) $ นั้นกำหนดโดย -

$$ \ sum_ {n = - \ infty} ^ \ infty (\ cos \ omega n) Z ^ {- n} = (Z ^ 2-Z \ cos \ omega) / (Z ^ 2-2Z \ cos \ โอเมก้า +1) $$

ตอนนี้ใช้คุณสมบัติ Time scaling การแปลง Z ของ $ a ^ n \ cos \ omega n $ สามารถเขียนเป็น;

$ \ sum_ {n = - \ infty} ^ \ infty (a ^ n \ cos \ omega n) Z ^ {- n} = X (a ^ {- 1} Z) $

$ = [(a ^ {- 1} Z) ^ 2- (a ^ {- 1} Z \ cos \ omega n)] / ((a ^ {- 1} Z) ^ 2-2 (a ^ {- 1} Z \ cos \ omega n) +1) $

$ = Z (Za \ cos \ โอเมก้า) / (Z ^ 2-2az \ cos \ โอเมก้า + ก ^ 2) $

ความแตกต่างอย่างต่อเนื่อง

คุณสมบัติความแตกต่างแบบต่อเนื่องแสดงให้เห็นว่าการแปลง Z จะเกิดขึ้นเมื่อเราแยกความแตกต่างของสัญญาณที่ไม่ต่อเนื่องในโดเมนเวลาตามเวลา ดังแสดงด้านล่าง

$$ \ frac {dx (n)} {dn} = (1-Z ^ {- 1}) X (Z) $$

Proof -

พิจารณา LHS ของสมการ - $ \ frac {dx (n)} {dn} $

$$ = \ frac {[x (n) -x (n-1)]} {[n- (n-1)]} $$

$ = x (n) -X (n-1) $

$ = x (Z) -Z ^ {- 1} x (Z) $

$ = (1-Z ^ {- 1}) x (Z) $ (ดังนั้นจึงพิสูจน์แล้ว)

ROC: R1 <Mod (Z) <R2

ตัวอย่าง

ให้เราค้นหาการแปลง Z ของสัญญาณที่กำหนดโดย $ x (n) = n ^ 2u (n) $

ตามคุณสมบัติเราสามารถเขียน

$ Zz [nU (n)] = -Z \ frac {dZ [U (n)]} {dz} $

$ = -Z \ frac {d [\ frac {Z} {Z-1}]} {dZ} $

$ = Z / ((Z-1) ^ 2 $

$ = y (ให้) $

ตอนนี้ Z [ny] สามารถพบได้โดยการใช้คุณสมบัติอีกครั้ง

$ Z (n, y) = -Z \ frac {dy} {dz} $

$ = -Z \ frac {d [Z / (Z-1) ^ 3]} {dz} $

$ = Z (Z + 1) / (Z-1) ^ 2 $

การแปลง

สิ่งนี้แสดงให้เห็นถึงการเปลี่ยนแปลงในโดเมน Z ของระบบเมื่อเกิด Convolution ในรูปแบบสัญญาณที่ไม่ต่อเนื่องซึ่งสามารถเขียนเป็น -

$ x_1 (n) * x_2 (n) \ longleftrightarrow X_1 (Z) .X_2 (Z) $

Proof -

$ X (Z) = \ sum_ {n = - \ infty} ^ \ infty x (n) Z ^ {- n} $

$ = \ sum_ {n = - \ infty} ^ \ infty [\ sum_ {k = - \ infty} ^ \ infty x_1 (k) x_2 (nk)] Z ^ {- n} $

$ = \ sum_ {k = - \ infty} ^ \ infty x_1 (k) [\ sum_n ^ \ infty x_2 (nk) Z ^ {- n}] $

$ = \ sum_ {k = - \ infty} ^ \ infty x_1 (k) [\ sum_ {n = - \ infty} ^ \ infty x_2 (nk) Z ^ {- (nk)} Z ^ {- k}] $

ให้ nk = l จากนั้นสมการด้านบนจะเขียนเป็น -

$ X (Z) = \ sum_ {k = - \ infty} ^ \ infty x_1 (k) [Z ^ {- k} \ sum_ {l = - \ infty} ^ \ infty x_2 (l) Z ^ {- l }] $

$ = \ sum_ {k = - \ infty} ^ \ infty x_1 (k) X_2 (Z) Z ^ {- k} $

$ = X_2 (Z) \ sum_ {k = - \ infty} ^ \ infty x_1 (Z) Z ^ {- k} $

$ = X_1 (Z) .X_2 (Z) $ (ดังนั้นพิสูจน์แล้ว)

ROC: $ ROC \ bigcap ROC2 $

ตัวอย่าง

ให้เราค้นหาการประชุมที่ได้รับจากสองสัญญาณ

$ x_1 (n) = \ lbrace 3, -2,2 \ rbrace $ ... (eq. 1)

$ x_2 (n) = \ lbrace 2,0 \ leq 4 \ quad และ \ quad 0 \ quad ที่อื่น \ rbrace $ ... (eq. 2)

การแปลง Z ของสมการแรกสามารถเขียนเป็น;

$ \ sum_ {n = - \ infty} ^ \ infty x_1 (n) Z ^ {- n} $

$ = 3-2Z ^ {- 1} + 2Z ^ {- 2} $

การแปลง Z ของสัญญาณที่สองสามารถเขียนเป็น;

$ \ sum_ {n = - \ infty} ^ \ infty x_2 (n) Z ^ {- n} $

$ = 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {- 4} $

ดังนั้นการแปลงสัญญาณทั้งสองข้างต้นจะได้รับโดย -

$ X (Z) = [x_1 (Z) ^ * x_2 (Z)] $

$ = [3-2Z ^ {- 1} + 2Z ^ {- 2}] \ times [2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {- 4 }] $

$ = 6 + 2Z ^ {- 1} + 6Z ^ {- 2} + 6Z ^ {- 3} + ... \ quad ... \ quad ... $

การแปลง Z แบบผกผันที่เราได้รับ

$ x (n) = \ lbrace 6,2,6,6,6,0,4 \ rbrace $

ทฤษฎีบทค่าเริ่มต้น

ถ้า x (n) เป็นลำดับเชิงสาเหตุซึ่งมีการแปลง Z เป็น X (z) ดังนั้นทฤษฎีบทค่าเริ่มต้นสามารถเขียนเป็น;

$ X (n) (ที่ \ quad n = 0) = \ lim_ {z \ to \ infty} X (z) $

Proof - เรารู้ว่า

$ X (Z) = \ sum_ {n = 0} ^ \ infty x (n) Z ^ {- n} $

ขยายชุดด้านบนเราได้รับ;

$ = X (0) Z ^ 0 + X (1) Z ^ {- 1} + X (2) Z ^ {- 2} + ... \ quad ... $

$ = X (0) \ คูณ 1 + X (1) Z ^ {- 1} + X (2) Z ^ {- 2} + ... \ quad ... $

ในกรณีข้างต้นถ้า Z →∞แล้ว $ Z ^ {- n} \ rightarrow 0 $ (เพราะ n> 0)

ดังนั้นเราสามารถพูด;

$ \ lim_ {z \ to \ infty} X (z) = X (0) $ (ดังนั้นจึงพิสูจน์แล้ว)

ทฤษฎีบทมูลค่าสุดท้าย

ทฤษฎีบทค่าสุดท้ายระบุว่าหากการแปลง Z ของสัญญาณแสดงเป็น X (Z) และเสาทั้งหมดอยู่ในวงกลมค่าสุดท้ายจะแสดงเป็น x (n) หรือ X (∞) และสามารถเขียนเป็น -

$ X (\ infty) = \ lim_ {n \ to \ infty} X (n) = \ lim_ {z \ to 1} [X (Z) (1-Z ^ {- 1})] $

Conditions -

ใช้ได้กับระบบเชิงสาเหตุเท่านั้น
$ X (Z) (1-Z ^ {- 1}) $ ควรมีเสาอยู่ในวงกลมหน่วยในระนาบ Z

Proof - เรารู้ว่า

$ Z ^ + [x (n + 1) -x (n)] = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {- n} [x (n + 1) -x (น)] $

$ \ Rightarrow Z ^ + [x (n + 1)] - Z ^ + [x (n)] = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {- n} [x (n + 1) -x (n)] $

$ \ Rightarrow Z [X (Z) ^ + - x (0)] - X (Z) ^ + = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {- n} [x (n + 1) -x (n)] $

ที่นี่เราสามารถใช้คุณสมบัติขั้นสูงของการแปลง Z ด้านเดียวได้ ดังนั้นสมการข้างต้นสามารถเขียนใหม่ได้เป็น;

$ Z ^ + [x (n + 1)] = Z [X (2) ^ + - x (0) Z ^ 0] = Z [X (Z) ^ + - x (0)] $

ตอนนี้ใส่ z = 1 ในสมการข้างบนเราสามารถขยายสมการข้างบน -

$ \ lim_ {k \ to \ infty} {[x (1) -x (0) + x (6) -x (1) + x (3) -x (2) + ... \ quad ... \ quad ... + x (x + 1) -x (k)]} $

สามารถกำหนดเป็น;

$ X (\ infty) = \ lim_ {n \ to \ infty} X (n) = \ lim_ {z \ to 1} [X (Z) (1-Z ^ {- 1})] $ (ดังนั้นจึงพิสูจน์แล้ว)

ตัวอย่าง

ให้เราหาค่าเริ่มต้นและค่าสุดท้ายของ x (n) ซึ่งสัญญาณถูกกำหนดโดย

$ X (Z) = 2 + 3Z ^ {- 1} + 4Z ^ {- 2} $

Solution - ก่อนอื่นให้เราหาค่าเริ่มต้นของสัญญาณโดยใช้ทฤษฎีบท

$ x (0) = \ lim_ {z \ to \ infty} X (Z) $

$ = \ lim_ {z \ to \ infty} [2 + 3Z ^ {- 1} + 4Z ^ {- 2}] $

$ = 2 + (\ frac {3} {\ infty}) + (\ frac {4} {\ infty}) = 2 $

ตอนนี้ให้เราหาค่าสุดท้ายของสัญญาณที่ใช้ทฤษฎีบท

$ x (\ infty) = \ lim_ {z \ to \ infty} [(1-Z ^ {- 1}) X (Z)] $

$ = \ lim_ {z \ to \ infty} [(1-Z ^ {- 1}) (2 + 3Z ^ {- 1} + 4Z ^ {- 2})] $

$ = \ lim_ {z \ to \ infty} [2 + Z ^ {- 1} + Z ^ {- 2} -4Z ^ {- 3}] $

$ = 2 + 1 + 1-4 = 0 $

Some other properties of Z-transform are listed below -

ความแตกต่างของความถี่

มันทำให้เกิดการเปลี่ยนแปลงในโดเมน Z ของสัญญาณเมื่อสัญญาณที่ไม่ต่อเนื่องแตกต่างกันไปตามเวลา

$ nx (n) \ longleftrightarrow -Z \ frac {dX (z)} {dz} $

ROC สามารถเขียนเป็น;

$ r_2 <Mod (Z) <r_1 $

ตัวอย่าง

ให้เราหาค่าของ x (n) ผ่านความแตกต่างของความถี่ซึ่งสัญญาณที่ไม่ต่อเนื่องในโดเมน Z จะได้รับโดย $ x (n) \ longleftrightarrow X (Z) = log (1 + aZ ^ {- 1}) $

ตามคุณสมบัติเราสามารถเขียนสิ่งนั้นได้

$ nx (n) \ longleftrightarrow -Z \ frac {dx (Z)} {dz} $

$ = -Z [\ frac {-aZ ^ {- 2}} {1 + aZ ^ {- 1}}] $

$ = (aZ ^ {- 1}) / (1 + aZ ^ {- 1}) $

$ = 1-1 / (1 + aZ ^ {- 1}) $

$ nx (n) = \ delta (n) - (- a) ^ nu (n) $

$ \ Rightarrow x (n) = 1 / n [\ delta (n) - (- ก) ^ nu (n)] $