DSP - การดำเนินการกับการแปลงสัญญาณ
การแปลงสัญญาณสองสัญญาณในโดเมนเวลาเทียบเท่ากับการคูณของการแทนค่าในโดเมนความถี่ ในทางคณิตศาสตร์เราสามารถเขียนการแปลงสัญญาณสองสัญญาณเป็น
$$ y (t) = x_ {1} (t) * x_ {2} (t) $$ $$ = \ int _ {- \ infty} ^ {\ infty} x_ {1} (p) .x_ {2 } (tp) dp $$ขั้นตอนในการ Convolution
- รับสัญญาณ x 1 (t) และใส่ t = p ที่นั่นเพื่อให้เป็น x 1 (p)
- รับสัญญาณ x 2 (t) และทำขั้นตอนที่ 1 และทำให้เป็น x 2 (p)
- ทำการพับสัญญาณคือ x 2 (-p)
- ทำการเปลี่ยนเวลาของสัญญาณด้านบน x 2 [- (pt)]
- จากนั้นทำการคูณของสัญญาณทั้งสอง คือ $ x_ {1} (p) .x_ {2} [- (p − t)] $
ตัวอย่าง
ให้เราทำการแปลงสัญญาณขั้นตอน u (t) ด้วยชนิดของมันเอง
$ y (t) = u (t) * u (t) $
$ = \ int _ {- \ infty} ^ {\ infty} [u (p) .u [- (pt)] dp $
ตอนนี้ t สามารถมากกว่าหรือน้อยกว่าศูนย์ซึ่งแสดงในรูปด้านล่าง
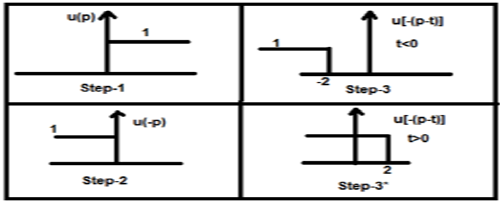
ดังนั้นจากกรณีข้างต้นผลลัพธ์จึงเกิดขึ้นตามความเป็นไปได้ดังต่อไปนี้
$ y (t) = \ begin {cases} 0, & if \ quad t <0 \\\ int_ {0} ^ {t} 1dt, & for \ quad t> 0 \ end {cases} $
$ = \ start {cases} 0, & if \ quad t <0 \\ t, & t> 0 \ end {cases} = r (t) $
คุณสมบัติของ Convolution
สับเปลี่ยน
มันระบุว่าลำดับการแปลงไม่สำคัญซึ่งสามารถแสดงทางคณิตศาสตร์เป็น
$$ x_ {1} (t) * x_ {2} (t) = x_ {2} (t) * x_ {1} (t) $$Associative
มันระบุว่าลำดับของการสนทนาที่เกี่ยวข้องกับสามสัญญาณอาจเป็นอะไรก็ได้ ในทางคณิตศาสตร์สามารถแสดงเป็น;
$$ x_ {1} (t) * [x_ {2} (t) * x_ {3} (t)] = [x_ {1} (t) * x_ {2} (t)] * x_ {3} (t) $$แจกจ่าย
สามารถเพิ่มสัญญาณสองสัญญาณก่อนจากนั้นจึงสามารถแปลงสัญญาณเป็นสัญญาณที่สามได้ สิ่งนี้เทียบเท่ากับการแปลงสัญญาณสองสัญญาณทีละสัญญาณกับสัญญาณที่สามและเพิ่มในที่สุด ในทางคณิตศาสตร์สามารถเขียนเป็น;
$$ x_ {1} (t) * [x_ {2} (t) + x_ {3} (t)] = [x_ {1} (t) * x_ {2} (t) + x_ {1} ( t) * x_ {3} (t)] $$พื้นที่
หากสัญญาณเป็นผลมาจากการแปลงสัญญาณสองสัญญาณพื้นที่ของสัญญาณจะเป็นการคูณของสัญญาณแต่ละตัว ในทางคณิตศาสตร์สามารถเขียนได้
ถ้า$ y (t) = x_ {1} * x_ {2} (t) $
จากนั้นพื้นที่ของ y (t) = พื้นที่ของ x 1 (t) X พื้นที่ของ x 2 (t)
การปรับขนาด
หากสัญญาณสองสัญญาณถูกปรับขนาดเป็นค่าคงที่ที่ไม่รู้จัก“ a” และการ Convolution เสร็จสิ้นสัญญาณผลลัพธ์จะถูกแปลงเป็นค่าคงที่เหมือนกัน“ a” และจะหารด้วยปริมาณดังที่แสดงด้านล่าง
ถ้า$ x_ {1} (t) * x_ {2} (t) = y (t) $
จากนั้น$ x_ {1} (at) * x_ {2} (at) = \ frac {y (at)} {a} a \ ne 0 $
ล่าช้า
สมมติว่าสัญญาณ y (t) เป็นผลมาจากการแปลงสัญญาณสองสัญญาณ x1 (t) และ x2 (t) หากสัญญาณทั้งสองล่าช้าตามเวลา t1 และ t2 ตามลำดับสัญญาณผลลัพธ์ y (t) จะล่าช้าโดย (t1 + t2) ในทางคณิตศาสตร์สามารถเขียนเป็น -
ถ้า$ x_ {1} (t) * x_ {2} (t) = y (t) $
จากนั้น$ x_ {1} (t-t_ {1}) * x_ {2} (t-t_ {2}) = y [t- (t_ {1} + t_ {2})] $
ตัวอย่างที่แก้ไข
Example 1 - ค้นหาการแปลงสัญญาณ u (t-1) และ u (t-2)
Solution- สัญญาณที่ให้คือ u (t-1) และ u (t-2) การสนทนาของพวกเขาสามารถทำได้ดังที่แสดงด้านล่าง
$ y (t) = u (t-1) * u (t-2) $
$ y (t) = \ int _ {- \ infty} ^ {+ \ infty} [u (t-1) .u (t-2)] dt $
$ = r (t-1) + r (t-2) $
$ = r (t-3) $
Example 2 - ค้นหาการแปลงสัญญาณสองสัญญาณที่กำหนดโดย
$x_{1}(n) = \lbrace 3,-2, 2\rbrace $
$ x_ {2} (n) = \ begin {cases} 2, & 0 \ leq n \ leq 4 \\ 0, & x> ที่อื่น \ end {cases} $
Solution -
x 2 (n) สามารถถอดรหัสเป็น $ x_ {2} (n) = \ lbrace 2,2,2,2,2 \ rbrace Originalfirst $
x 1 (n) ก่อนหน้านี้ได้รับ $ = \ lbrace 3, -2,3 \ rbrace = 3-2Z ^ {- 1} + 2Z ^ {- 2} $
ในทำนองเดียวกัน$ x_ {2} (z) = 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {- 4} $
สัญญาณผลลัพธ์
$ X (Z) = X_ {1} (Z) X_ {2} (z) $
$ = \ lbrace 3-2Z ^ {- 1} + 2Z ^ {- 2} \ rbrace \ times \ lbrace 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {-4} \ rbrace $
$ = 6 + 2Z ^ {- 1} + 6Z ^ {- 2} + 6Z ^ {- 3} + 6Z ^ {- 4} + 6Z ^ {- 5} $
การแปลง Z แบบผกผันข้างต้นเราจะได้สัญญาณผลลัพธ์เป็น
$ x (n) = \ lbrace 6,2,6,6,6,0,4 \ rbrace $ Origin ในตอนแรก
Example 3 - กำหนด Convolution ของ 2 สัญญาณต่อไปนี้ -
$x(n) = \lbrace 2,1,0,1\rbrace$
$h(n) = \lbrace 1,2,3,1\rbrace$
Solution -
เราได้รับการแปลงสัญญาณ Z
$ x (z) = 2 + 2Z ^ {- 1} + 2Z ^ {- 3} $
และ$ h (n) = 1 + 2Z ^ {- 1} + 3Z ^ {- 2} + Z ^ {- 3} $
ตอนนี้การแปลงสัญญาณสองสัญญาณหมายถึงการคูณการแปลง Z ของพวกเขา
นั่นคือ$ Y (Z) = X (Z) \ times h (Z) $
$ = \ lbrace 2 + 2Z ^ {- 1} + 2Z ^ {- 3} \ rbrace \ times \ lbrace 1 + 2Z ^ {- 1} + 3Z ^ {- 2} + Z ^ {- 3} \ rbrace $
$ = \ lbrace 2 + 5Z ^ {- 1} + 8Z ^ {- 2} + 6Z ^ {- 3} + 3Z ^ {- 4} + 3Z ^ {- 5} + Z ^ {- 6} \ rbrace $
การแปลง Z แบบผกผันสัญญาณผลลัพธ์สามารถเขียนเป็น;
$ y (n) = \ lbrace 2,5,8,6,6,1 \ rbrace Originalfirst $