การประมวลผลสัญญาณดิจิทัล - สัญญาณ DT พื้นฐาน

เราได้เห็นว่าสัญญาณพื้นฐานสามารถแสดงในโดเมนเวลาต่อเนื่องได้อย่างไร ให้เราดูว่าสัญญาณพื้นฐานสามารถแสดงใน Discrete Time Domain ได้อย่างไร

ลำดับอิมพัลส์หน่วย

แสดงเป็นδ (n) ในโดเมนเวลาไม่ต่อเนื่องและสามารถกำหนดเป็น;

$$ \ delta (n) = \ begin {cases} 1, & for \ quad n = 0 \\ 0, & มิฉะนั้น \ end {cases} $$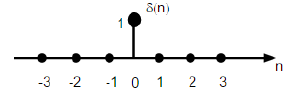

สัญญาณขั้นตอนของหน่วย

สัญญาณขั้นตอนหน่วยเวลาไม่ต่อเนื่องถูกกำหนดให้เป็น;

$$ U (n) = \ begin {cases} 1, & for \ quad n \ geq0 \\ 0, & for \ quad n <0 \ end {cases} $$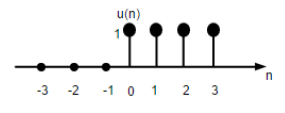

รูปด้านบนแสดงการแสดงกราฟิกของฟังก์ชันขั้นตอนที่ไม่ต่อเนื่อง

ฟังก์ชัน Unit Ramp

ฟังก์ชันทางลาดหน่วยแยกสามารถกำหนดเป็น -

$$ r (n) = \ begin {cases} n, & for \ quad n \ geq0 \\ 0, & for \ quad n <0 \ end {cases} $$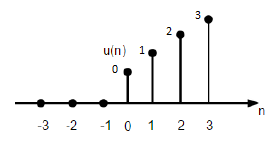

รูปที่ให้ไว้ด้านบนแสดงการแสดงกราฟิกของสัญญาณทางลาดที่ไม่ต่อเนื่อง

ฟังก์ชันพาราโบลา

ฟังก์ชันพาราโบลาของหน่วยไม่ต่อเนื่องแสดงเป็น p (n) และสามารถกำหนดเป็น;

$$ p (n) = \ begin {cases} \ frac {n ^ {2}} {2}, & สำหรับ \ quad n \ geq0 \\ 0, & สำหรับ \ quad n <0 \ end {cases} $$

ในแง่ของฟังก์ชันขั้นตอนหน่วยสามารถเขียนเป็น;

$$ P (n) = \ frac {n ^ {2}} {2} U (n) $$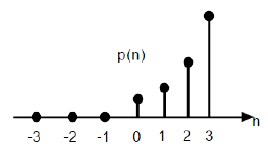

รูปที่ให้ไว้ด้านบนแสดงการแสดงกราฟิกของลำดับพาราโบลา

สัญญาณไซน์

สัญญาณเวลาต่อเนื่องทั้งหมดเป็นระยะ ลำดับไซน์ไทม์ที่ไม่ต่อเนื่องอาจเป็นระยะหรือไม่ก็ได้ ขึ้นอยู่กับค่าของω เพื่อให้สัญญาณเวลาไม่ต่อเนื่องเป็นคาบความถี่เชิงมุมωต้องเป็นตัวคูณที่มีเหตุผลของ2π