DSP - การดำเนินการเกี่ยวกับการปรับขนาดสัญญาณ
การสเกลของสัญญาณหมายถึงค่าคงที่จะคูณกับเวลาหรือแอมพลิจูดของสัญญาณ
การปรับเวลา
ถ้าค่าคงที่คูณกับแกนเวลาจะเรียกว่าการปรับเวลา สิ่งนี้สามารถแทนค่าทางคณิตศาสตร์เป็น;
$ x (t) \ rightarrow y (t) = x (\ alpha t) $ หรือ $ x (\ frac {t} {\ alpha}) $; โดยที่α≠ 0
ดังนั้นแกน y เท่ากันขนาดแกน x จะลดลงหรือเพิ่มขึ้นตามสัญลักษณ์ของค่าคงที่ (ไม่ว่าจะเป็นบวกหรือลบ) ดังนั้นการปรับขนาดจึงสามารถแบ่งออกเป็นสองประเภทตามที่กล่าวไว้ด้านล่าง
การบีบอัดเวลา
เมื่อใดก็ตามที่อัลฟ่ามีค่ามากกว่าศูนย์แอมพลิจูดของสัญญาณจะถูกหารด้วยอัลฟาในขณะที่ค่าของแกน Y ยังคงเท่าเดิม ซึ่งเรียกว่าการบีบอัดเวลา
Example
ให้เราพิจารณาสัญญาณ x (t) ซึ่งแสดงดังรูปด้านล่าง ให้เราหาค่าของอัลฟ่าเป็น 2 ดังนั้น y (t) จะเป็น x (2t) ซึ่งแสดงในรูปที่กำหนด

เห็นได้ชัดจากตัวเลขด้านบนว่าขนาดของเวลาในแกน y ยังคงเท่าเดิม แต่แอมพลิจูดในแกน x ลดลงจาก 4 เป็น 2 ดังนั้นจึงเป็นกรณีของการบีบอัดเวลา
การขยายเวลา
เมื่อเวลาถูกหารด้วยอัลฟ่าคงที่ขนาดแกน Y ของสัญญาณจะได้รับคูณอัลฟาคูณโดยรักษาขนาดแกน X ตามที่เป็นอยู่ ดังนั้นจึงเรียกว่าสัญญาณประเภทการขยายเวลา
Example
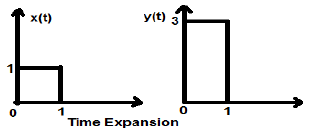
ให้เราพิจารณาสัญญาณกำลังสอง x (t) ขนาด 1 เมื่อเรากำหนดเวลาด้วยค่าคงที่ 3 เช่น $ x (t) \ rightarrow y (t) \ rightarrow x (\ frac {t} {3} ) $ จากนั้นแอมพลิจูดของสัญญาณจะถูกแก้ไข 3 ครั้งซึ่งแสดงในรูปด้านล่าง
การปรับขนาดความกว้าง
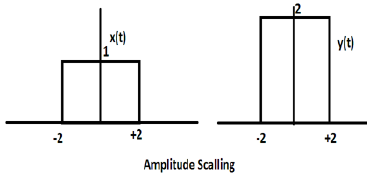
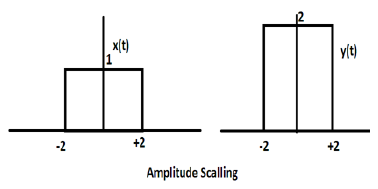
การคูณค่าคงที่ด้วยแอมพลิจูดของสัญญาณทำให้เกิดการปรับขนาดแอมพลิจูด ขึ้นอยู่กับสัญลักษณ์ของค่าคงที่อาจเป็นได้ทั้งการปรับขนาดแอมพลิจูดหรือการลดทอน ให้เราพิจารณาสัญญาณคลื่นสี่เหลี่ยม x (t) = Π (t / 4)
สมมติว่าเรากำหนดฟังก์ชันอื่น y (t) = 2 Π (t / 4) ในกรณีนี้ค่าของแกน y จะเพิ่มขึ้นเป็นสองเท่าโดยรักษาค่าแกนเวลาไว้ตามเดิม แสดงในรูปด้านล่าง
พิจารณาฟังก์ชันคลื่นสี่เหลี่ยมอื่นที่กำหนดเป็น z (t) โดยที่ z (t) = 0.5 Π (t / 4) ที่นี่แอมพลิจูดของฟังก์ชัน z (t) จะเป็นครึ่งหนึ่งของ x (t) คือแกนเวลายังคงเท่าเดิมแกนแอมพลิจูดจะลดลงครึ่งหนึ่ง นี่คือภาพประกอบที่แสดงด้านล่าง