Thống kê - Định lý giới hạn trung tâm

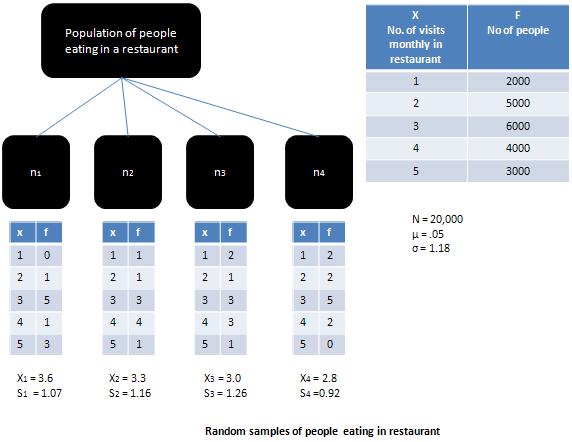
Nếu quần thể mà từ đó mẫu được rút ra là một quần thể bình thường thì sample means sẽ bằng trung bình dân số và sampling distributionsẽ là bình thường. Khi dân số nhiều hơn bị lệch, như trường hợp được minh họa trong Hình, thìsampling distribution sẽ có xu hướng tiến gần đến phân phối chuẩn, miễn là mẫu lớn (tức là lớn hơn 30).

Dựa theo Central Limit Theorem, đối với các mẫu đủ lớn có kích thước lớn hơn 30, hình dạng của sampling distribution sẽ ngày càng trở nên giống như một normal distribution, không phân biệt hình dạng của quần thể mẹ. Định lý này giải thích mối quan hệ giữapopulation distribution và sampling distribution. Nó làm nổi bật thực tế là nếu có bộ mẫu đủ lớn thìsampling distribution phương pháp tiếp cận trung bình normal distribution. Tầm quan trọng của định lý giới hạn trung tâm đã được Richard tổng kết. I. Levin trong những từ sau:

Ý nghĩa của định lý giới hạn trung tâm nằm ở chỗ nó cho phép chúng ta sử dụng số liệu thống kê mẫu để đưa ra suy luận về các tham số dân số mà không cần biết gì về hình dạng của phân bố tần số của tổng thể đó ngoài những gì chúng ta có thể nhận được từ mẫu.