Thống kê - Phân phối F
Phân phối F (phân phối F của Snedecor hoặc phân phối Fisher-Snedecor) đại diện cho phân phối xác suất liên tục xảy ra thường xuyên dưới dạng phân phối rỗng của thống kê thử nghiệm. Nó xảy ra chủ yếu trong quá trình phân tích phương sai hoặc F-test.
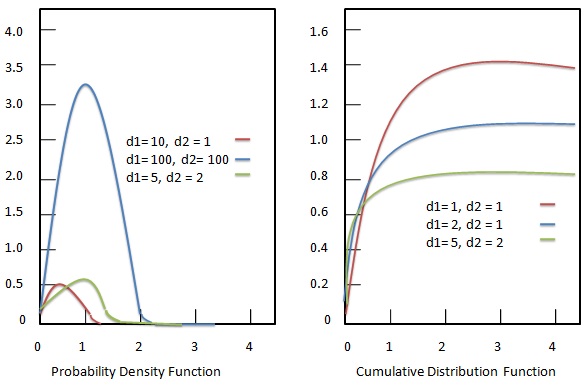
Hàm mật độ xác suất
Hàm mật độ xác suất của phân phối F được cho là:
Công thức
$ {f (x; d_1, d_2) = \ frac {\ sqrt {\ frac {(d_1 x) ^ {d_1} d_2 ^ {d_2}} {(d_1x + d_2) ^ {d_1 + d_2}}}} { x \ beta (\ frac {d_1} {2}, \ frac {d_2} {2})}} $
Ở đâu -
$ {d_1} $ = tham số dương.
$ {d_2} $ = tham số dương.
$ {x} $ = biến ngẫu nhiên.
Chức năng phân phối tích lũy
Hàm phân phối tích lũy của phân phối F được cho là:
Công thức
$ {F (x; d_1, d_2) = I _ {\ frac {d_1x} {d_1x + d_2}} (\ frac {d_1} {2}, \ frac {d_2} {2})} $
Ở đâu -
$ {d_1} $ = tham số dương.
$ {d_2} $ = tham số dương.
$ {x} $ = biến ngẫu nhiên.
$ {I} $ = chức năng beta chưa hoàn thành thấp hơn.