Thống kê - Hồi quy Logistic

Hồi quy logistic là một phương pháp thống kê để phân tích một tập dữ liệu trong đó có một hoặc nhiều biến độc lập xác định một kết quả. Kết quả được đo bằng một biến phân đôi (trong đó chỉ có hai kết quả có thể xảy ra).

Công thức

$ {\ pi (x) = \ frac {e ^ {\ alpha + \ beta x}} {1 + e ^ {\ alpha + \ beta x}}} $

Ở đâu -

Phản hồi - Sự hiện diện / Sự vắng mặt của đặc tính.
Dự đoán - Biến số được quan sát cho từng trường hợp
$ {\ beta = 0 \ Rightarrow} $ P (Hiện diện) giống nhau ở mỗi cấp của x.
$ {\ beta \ gt 0 \ Rightarrow} $ P (Hiện diện) tăng khi x tăng
$ {\ beta = 0 \ Rightarrow} $ P (Hiện diện) giảm khi x tăng.

Thí dụ

Problem Statement:

Giải quyết hồi quy logistic của vấn đề sau Rizatriptan for Migraine

Phản hồi - Giảm đau hoàn toàn sau 2 giờ (Có / Không).

Dự đoán - Liều lượng (mg): Giả dược (0), 2,5,5,10

Liều lượng	#Người bệnh	#An tâm	%An tâm
0	67	2	3.0
2,5	75	7	9.3
5	130	29	22.3
10	145	40	27,6

Solution:

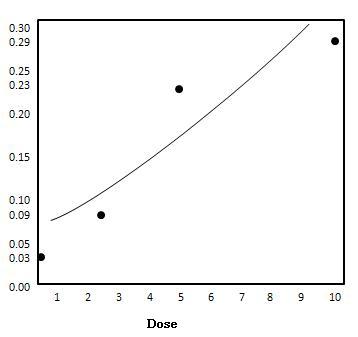
Có $ {\ alpha = -2.490} và $ {\ beta = .165}, chúng tôi có dữ liệu sau:

$ {\ pi (0) = \ frac {e ^ {\ alpha + \ beta \ times 0}} {1 + e ^ {\ alpha + \ beta \ times 0}} \\ [7pt] \, = \ frac {e ^ {- 2.490 + 0}} {1 + e ^ {- 2.490}} \\ [7pt] \\ [7pt] \, = 0.03 \\ [7pt] \ pi (2.5) = \ frac {e ^ {\ alpha + \ beta \ times 2.5}} {1 + e ^ {\ alpha + \ beta \ times 2.5}} \\ [7pt] \, = \ frac {e ^ {- 2.490 + .165 \ times 2.5} } {1 + e ^ {- 2.490 + .165 \ times 2.5}} \\ [7pt] \, = 0.09 \\ [7pt] \\ [7pt] \ pi (5) = \ frac {e ^ {\ alpha + \ beta \ times 5}} {1 + e ^ {\ alpha + \ beta \ times 5}} \\ [7pt] \, = \ frac {e ^ {- 2.490 + .165 \ times 5}} {1 + e ^ {- 2.490 + .165 \ times 5}} \\ [7pt] \, = 0.23 \\ [7pt] \\ [7pt] \ pi (10) = \ frac {e ^ {\ alpha + \ beta \ times 10}} {1 + e ^ {\ alpha + \ beta \ times 10}} \\ [7pt] \, = \ frac {e ^ {- 2.490 + .165 \ times 10}} {1 + e ^ {-2.490 + .165 \ times 10}} \\ [7pt] \, = 0.29} $

Liều ($ {x} $)	$ {\ pi (x)} $
0	0,03
2,5	0,09
5	0,23
10	0,29