Thống kê - Phân phối hàm mũ
Phân phối mũ hoặc phân phối mũ âm đại diện cho một phân phối xác suất để mô tả thời gian giữa các sự kiện trong một quá trình Poisson. Trong quá trình Poisson, các sự kiện xảy ra liên tục và độc lập với tốc độ trung bình không đổi. Phân phối hàm mũ là một trường hợp cụ thể của phân phối gamma.
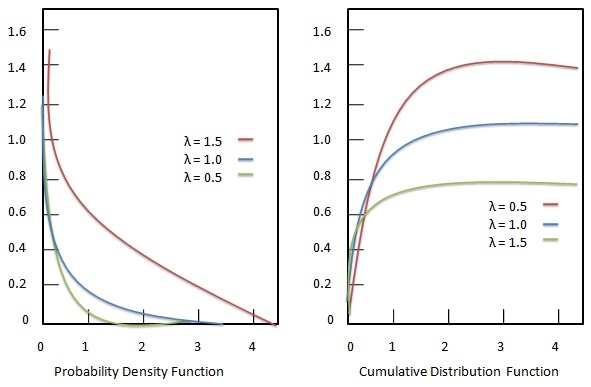
Hàm mật độ xác suất
Hàm mật độ xác suất của phân phối mũ được cho là:
Công thức
$ {f (x; \ lambda) =} $ $ \ begin {case} \ lambda e ^ {- \ lambda x}, & \ text {if $ x \ ge 0 $} \\ [7pt] 0, & \ nhắn tin {if $ x \ lt 0 $} \ end {case} $
Ở đâu -
$ {\ lambda} $ = tham số tỷ lệ.
$ {x} $ = biến ngẫu nhiên.
Chức năng phân phối tích lũy
Hàm phân phối tích lũy của phân phối mũ được cho là:
Công thức
$ {F (x; \ lambda) =} $ $ \ begin {case} 1- e ^ {- \ lambda x}, & \ text {if $ x \ ge 0 $} \\ [7pt] 0, & \ nhắn tin {if $ x \ lt 0 $} \ end {case} $
Ở đâu -
$ {\ lambda} $ = tham số tỷ lệ.
$ {x} $ = biến ngẫu nhiên.