Thống kê - Phân phối Poisson tích lũy
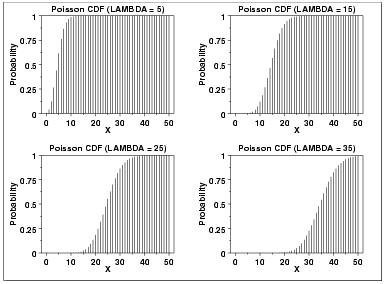
$ {\ lambda} $ là tham số hình dạng cho biết số lượng sự kiện trung bình trong khoảng thời gian nhất định. Sau đây là biểu đồ của hàm mật độ xác suất Poisson cho bốn giá trị của $ {\ lambda} $. Chức năng phân phối tích lũy.
Công thức
$$ {F (x, \ lambda) = \ sum_ {k = 0} ^ x \ frac {e ^ {- \ lambda} \ lambda ^ x} {k!}} $$
Ở đâu -
$ {e} $ = Cơ số của lôgarit tự nhiên bằng 2,71828
$ {k} $ = Số lần xuất hiện của một sự kiện; xác suất được cho bởi hàm.
$ {k!} $ = Giai thừa của k
$ {\ lambda} $ = Một số thực dương, bằng số lần xuất hiện dự kiến trong khoảng thời gian nhất định
Thí dụ
Problem Statement:
Một hệ thống phần mềm phức tạp trung bình có 7 lỗi trên 5.000 dòng mã. Xác suất để xảy ra đúng 2 lỗi trong 5.000 dòng mã được chọn ngẫu nhiên là bao nhiêu?
Solution:
Xác suất để có đúng 2 lỗi trong 5.000 dòng mã được chọn ngẫu nhiên là: