Thống kê - Kurtosis

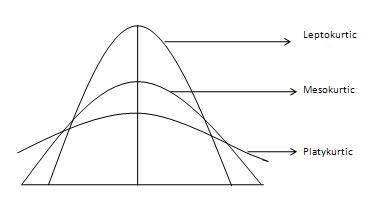
Mức độ liên kết của một phân phối được đo bằng kurtosis. Nó cho chúng ta biết mức độ mà phân phối nhiều hơn hoặc ít hơn ở bên ngoài (nặng hơn hoặc nhẹ hơn) so với phân phối chuẩn. Ba loại đường cong khác nhau, do Investopedia cung cấp, được hiển thị như sau:

Rất khó để phân biệt các loại kurtosis khác nhau từ các ô mật độ (bảng bên trái) vì các phần đuôi gần bằng 0 đối với tất cả các phân bố. Nhưng sự khác biệt ở các phần đuôi có thể dễ dàng nhận thấy trong các ô lượng tử-lượng tử thông thường (bảng bên phải).

Đường cong thông thường được gọi là đường cong Mesokurtic. Nếu đường cong của phân bố có xu hướng lệch hơn (hoặc có đuôi nặng hơn) so với đường cong bình thường hoặc đường trung bình thì nó được gọi là đường cong Leptokurtic. Nếu một đường cong ít bị lồi lõm (hoặc có đuôi nhạt hơn) so với đường cong bình thường, nó được gọi là đường cong mỏ vịt. Kurtosis được đo bằng khoảnh khắc và được tính theo công thức sau:

Công thức

$ {\ beta_2 = \ frac {\ mu_4} {\ mu_2}} $

Ở đâu -

$ {\ mu_4 = \ frac {\ sum (x- \ bar x) ^ 4} {N}} $

Giá trị của \ beta_2 càng lớn thì đường cong càng có giá trị cực đại hoặc có độ dài. Đường cong bình thường có giá trị là 3, leptokurtic có \ beta_2 lớn hơn 3 và Platykurtic có \ beta_2 nhỏ hơn 3.

Thí dụ

Problem Statement:

Dữ liệu về tiền lương hàng ngày của 45 công nhân của một nhà máy được đưa ra. Tính toán \ beta_1 và \ beta_2 sử dụng thời điểm về giá trị trung bình. Nhận xét về kết quả.

Tiền lương (Rs.)	Số lượng công nhân
100-200	1
120-200	2
140-200	6
160-200	20
180-200	11
200-200	3
220-200	2

Solution:

Tiền lương (Rs.)	Số lượng công nhân (f)	Giữa pt m	m - $ {\ frac {170} {20}} $ d	$ {fd} $	$ {fd ^ 2} $	$ {fd ^ 3} $	$ {fd ^ 4} $
100-200	1	110	-3	-3	9	-27	81
120-200	2	130	-2	-4	số 8	-16	32
140-200	6	150	-1	-6	6	-6	6
160-200	20	170	0	0	0	0	0
180-200	11	190	1	11	11	11	11
200-200	3	210	2	6	12	24	48
220-200	2	230	3	6	18	54	162
	$ {N = 45} $			$ {\ sum fd = 10} $	$ {\ sum fd ^ 2 = 64} $	$ {\ sum fd ^ 3 = 40} $	$ {\ sum fd ^ 4 = 330} $

Vì độ lệch được lấy từ giá trị trung bình giả định, do đó, trước tiên chúng ta tính toán các khoảnh khắc về gốc tùy ý và sau đó là các khoảnh khắc về giá trị trung bình. Khoảnh khắc về nguồn gốc tùy ý '170'

$ {\ mu_1 ^ 1 = \ frac {\ sum fd} {N} \ times i = \ frac {10} {45} \ times 20 = 4,44 \\ [7pt] \ mu_2 ^ 1 = \ frac {\ sum fd ^ 2} {N} \ times i ^ 2 = \ frac {64} {45} \ times 20 ^ 2 = 568.88 \\ [7pt] \ mu_3 ^ 1 = \ frac {\ sum fd ^ 2} {N} \ times i ^ 3 = \ frac {40} {45} \ times 20 ^ 3 = 7111.11 \\ [7pt] \ mu_4 ^ 1 = \ frac {\ sum fd ^ 4} {N} \ times i ^ 4 = \ frac {330} {45} \ times 20 ^ 4 = 1173333,33} $

Khoảnh khắc về ý nghĩa

$ {\ mu_2 = \ mu'_2 - (\ mu'_1) ^ 2 = 568.88- (4.44) ^ 2 = 549.16 \\ [7pt] \ mu_3 = \ mu'_3 - 3 (\ mu'_1) (\ mu'_2) + 2 (\ mu'_1) ^ 3 \\ [7pt] \, = 7111.11 - (4.44) (568.88) + 2 (4.44) ^ 3 \\ [7pt] \, = 7111.11 - 7577.48 + 175.05 = - 291.32 \\ [7pt] \\ [7pt] \ mu_4 = \ mu'_4 - 4 (\ mu'_1) (\ mu'_3) + 6 (\ mu_1) ^ 2 (\ mu'_2) -3 (\ mu'_1) ^ 4 \\ [7pt] \, = 1173333.33 - 4 (4.44) (7111.11) +6 (4.44) ^ 2 (568.88) - 3 (4.44) ^ 4 \\ [7pt] \, = 1173333.33 - 126293.31 + 67288.03-1165.87 \\ [7pt] \, = 1113162.18} $

Từ giá trị của sự di chuyển về giá trị trung bình, giờ đây chúng tôi có thể tính được $ {\ beta_1} $ và $ {\ beta_2} $:

$ {\ beta_1 = \ mu ^ 2_3 = \ frac {(- 291,32) ^ 2} {(549,16) ^ 3} = 0,00051 \\ [7pt] \ beta_2 = \ frac {\ mu_4} {(\ mu_2) ^ 2 } = \ frac {1113162.18} {(546.16) ^ 2} = 3,69} $

Từ các tính toán trên, có thể kết luận rằng $ {\ beta_1} $, đo độ lệch gần như bằng 0, do đó cho thấy rằng phân phối gần như đối xứng. $ {\ beta_2} $ Đo lường kurtosis, có giá trị lớn hơn 3, do đó ngụ ý rằng phân phối là leptokurtic.