Statystyki - dystrybucja beta

Rozkład beta reprezentuje ciągły rozkład prawdopodobieństwa sparametryzowany przez dwa dodatnie parametry kształtu, $ \alpha $ i $ \beta $, które pojawiają się jako wykładniki zmiennej losowej x i kontrolują kształt rozkładu.

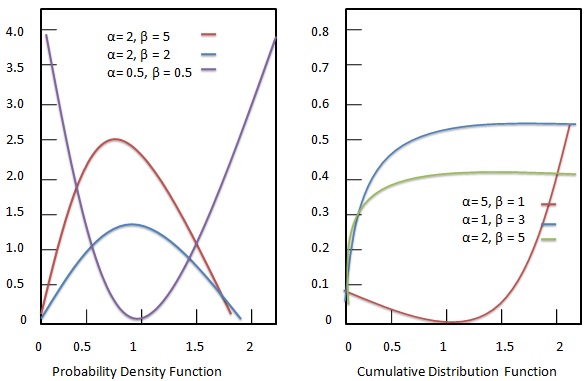
Funkcja gęstości prawdopodobieństwa

Funkcja gęstości prawdopodobieństwa rozkładu Beta jest podana jako:

Formuła

${ f(x) = \frac{(x-a)^{\alpha-1}(b-x)^{\beta-1}}{B(\alpha,\beta) (b-a)^{\alpha+\beta-1}} \hspace{.3in} a \le x \le b; \alpha, \beta > 0 \\[7pt] \, where \ B(\alpha,\beta) = \int_{0}^{1} {t^{\alpha-1}(1-t)^{\beta-1}dt} }$

Gdzie -

${ \alpha, \beta }$ = parametry kształtu.
${a, b}$ = górna i dolna granica.
${B(\alpha,\beta)}$ = Funkcja Beta.

Standardowa dystrybucja beta

W przypadku, gdy górna i dolna granica wynosi 1 i 0, rozkład beta nazywany jest standardowym rozkładem beta. Kieruje się następującym wzorem:

Formuła

${ f(x) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)} \hspace{.3in} \le x \le 1; \alpha, \beta > 0}$

Dystrybuanta

Dystrybucja skumulowana dystrybucji Beta jest podana jako:

Formuła

${ F(x) = I_{x}(\alpha,\beta) = \frac{\int_{0}^{x}{t^{\alpha-1}(1-t)^{\beta-1}dt}}{B(\alpha,\beta)} \hspace{.2in} 0 \le x \le 1; p, \beta > 0 }$

Gdzie -

${ \alpha, \beta }$ = parametry kształtu.
${a, b}$ = górna i dolna granica.
${B(\alpha,\beta)}$ = Funkcja Beta.

Nazywa się to również niepełnym współczynnikiem funkcji beta.

© Copyright 2021 - 2025 | All Rights Reserved