Statystyka - rozkład normalny
Rozkład normalny to układ zbioru danych, w którym większość wartości skupia się w środku zakresu, a reszta zmniejsza się symetrycznie w kierunku dowolnej skrajności. Wzrost jest jednym prostym przykładem czegoś, co jest zgodne z rozkładem normalnym: większość ludzi ma średni wzrost, liczba osób wyższych i niższych od średniej jest dość równa, a bardzo mała (i nadal z grubsza równoważna) liczba osób to albo bardzo wysoka lub bardzo krótka Oto przykład krzywej rozkładu normalnego:
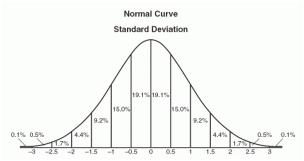
Graficzne przedstawienie rozkładu normalnego jest czasami nazywane krzywą dzwonową ze względu na jej rozszerzony kształt. Dokładny kształt może się różnić w zależności od rozmieszczenia populacji, ale szczyt jest zawsze pośrodku, a krzywa jest zawsze symetryczna. W rozkładzie normalnym tryb średni i mediana są takie same.
Formuła
$ {y = \ frac {1} {\ sqrt {2 \ pi}} e ^ {\ frac {- (x - \ mu) ^ 2} {2 \ sigma}}} $
Gdzie -
$ {\ mu} $ = średnia
$ {\ sigma} $ = odchylenie standardowe
$ {\ pi \ około 3,14159} $
$ {e \ około 2,71828} $
Przykład
Problem Statement:
Badanie dziennego czasu podróży dało następujące wyniki (w minutach):
| 26 | 33 | 65 | 28 | 34 | 55 | 25 | 44 | 50 | 36 | 26 | 37 | 43 | 62 | 35 | 38 | 45 | 32 | 28 | 34 |
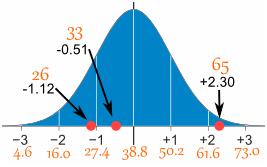
Średnia wynosi 38,8 minuty, a odchylenie standardowe wynosi 11,4 minuty. Zamień wartości na z-score i przygotuj wykres rozkładu normalnego.
Solution:
Wzór na z-score, którego używaliśmy:
$ {z = \ frac {x - \ mu} {\ sigma}} $
Gdzie -
$ {z} $ = „z-score” (standardowy wynik)
$ {x} $ = wartość do znormalizowania
$ {\ mu} $ = średnia
$ {\ sigma} $ = odchylenie standardowe
Aby przekonwertować 26:
Najpierw odejmij średnią: 26-38,8 = -12,8,
Następnie podziel przez odchylenie standardowe: -12,8 / 11,4 = -1,12
Czyli 26 to -1,12 odchylenie standardowe od średniej
Oto pierwsze trzy konwersje.
| Oryginalna wartość | Obliczenie | Wynik standardowy (wynik z) |
|---|---|---|
| 26 | (26-38,8) / 11,4 = | -1.12 |
| 33 | (33-38,8) / 11,4 = | -0,51 |
| 65 | (65-38,8) / 11,4 = | -2,30 |
| ... | ... | ... |
A tutaj graficznie przedstawiają: