Statystyki - wykresy pudełkowe
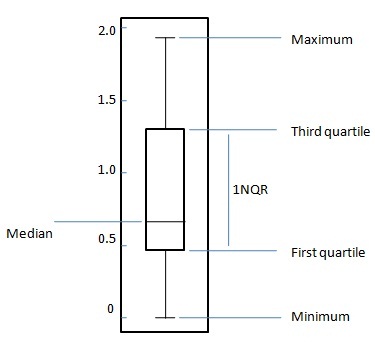
Wykres pudełkowy to ustandaryzowany sposób wyświetlania rozkładu danych w oparciu o poniższe podsumowanie pięciu liczb.
Minimum
Pierwszy kwartyl
Median
Trzeci kwartyl
Maximum
W przypadku równomiernie rozłożonego zestawu danych, na diagramie pudełkowym, centralny prostokąt obejmuje pierwszy kwartyl do trzeciego kwartylu (lub przedział międzykwartylowy, IQR). Linia wewnątrz prostokąta przedstawia medianę, a „wąsy” nad i pod ramką pokazują lokalizacje wartości minimalnych i maksymalnych. Taki wykres pudełkowy przedstawia pełny zakres zmienności od minimum do maksimum, prawdopodobny zakres zmienności, IQR i medianę.
Oświadczenie dotyczące problemu:
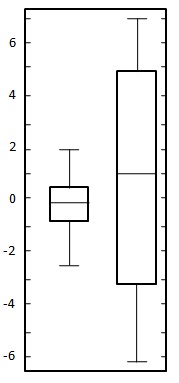
Utwórz wykres pudełkowy dla następujących dwóch zestawów danych.
| 0,22 |
| -0,87 |
| -2,39 |
| -1,79 |
| 0.37 |
| -1,54 |
| 1.28 |
| -0,31 |
| -0,74 |
| 1.72 |
| 0.38 |
| -0,17 |
| -0,62 |
| -1,10 |
| 0,30 |
| 0,15 |
| 2.30 |
| 0.19 |
| -0,50 |
| -0.09 |
| -5,13 |
| -2,19 |
| -2,43 |
| -3,83 |
| 0,50 |
| -3,25 |
| 4.32 |
| 1.63 |
| 5.18 |
| -0,43 |
| 7.11 |
| 4.87 |
| -3,10 |
| -5,81 |
| 3.76 |
| 6.31 |
| 2.58 |
| 0,07 |
| 5.76 |
| 3.50 |
Rozwiązanie:
Tutaj oba zbiory danych są równomiernie zrównoważone wokół zera, więc średnia wynosi około zera. W pierwszym zestawie danych waha się w przybliżeniu od -2,5 do 2,5, podczas gdy w drugim zestawie danych waha się w przybliżeniu od -6 do 6. Narysuj wykres, jak pokazano poniżej: