Statystyka - równanie regresji kwadratowej
Regresja kwadratowa służy do określenia równania paraboli, które najlepiej pasuje do danego zbioru danych. Ma następującą postać:
$ {y = ax ^ 2 + bx + c \ gdzie \ a \ ne 0} $
Do znalezienia równania regresji kwadratowej można użyć metody najmniejszych kwadratów. W tej metodzie obliczamy wartość a, b i c, tak aby kwadratowa odległość w pionie między każdym podanym punktem ($ {x_i, y_i} $) a równaniem paraboli ($ {y = ax ^ 2 + bx + 2} $) jest minimalna. Równanie macierzowe krzywej parabolicznej jest określone wzorem:
Współczynnik korelacji, r
Współczynnik korelacji r określa, jak dobrze równanie kwardratyczne może pasować do podanych danych. Jeśli r jest bliskie 1, to jest dobrze dopasowane. r można obliczyć za pomocą następującego wzoru.
$ {r = 1 - \ frac {SSE} {SST} \ gdzie \\ [7pt] \ SSE = \ sum (y_i - a {x_i} ^ 2 - bx + i - c) ^ 2 \\ [7pt] \ SST = \ sum (y_i - \ bar y) ^ 2} $
Ogólnie rzecz biorąc, kalkulatory regresji kwadratowej są używane do obliczania równania regresji kwadratowej.
Przykład
Problem Statement:
Oblicz równanie regresji kwadratowej następujących danych. Sprawdź jego najlepszą kondycję.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| y | 7.5 | 3 | 0.5 | 1 | 3 | 6 | 14 |
Solution:
Oblicz regresję kwadratową na kalkulatorze, umieszczając wartości x i y. Najlepiej dopasowane równanie kwadratowe dla powyższych punktów ma postać
$ {y = 1,1071x ^ 2 + 0,5714x} $
Aby sprawdzić najlepszą kondycję, wykreśl wykres.
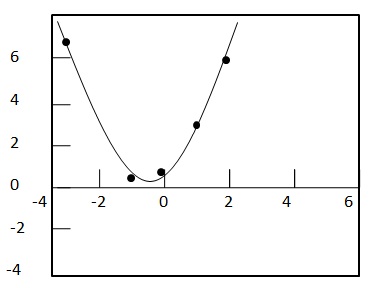
Zatem wartość współczynnika korelacji, r dla danych, wynosi 0,99420 i jest bliska 1. Stąd najlepiej pasuje równanie regresji kwadratowej.