Statystyka - regresja logistyczna
Regresja logistyczna to metoda statystyczna służąca do analizowania zbioru danych, w którym istnieje co najmniej jedna zmienna niezależna określająca wynik. Wynik mierzy się zmienną dychotomiczną (w której są tylko dwa możliwe wyniki).
Formuła
$ {\ pi (x) = \ frac {e ^ {\ alpha + \ beta x}} {1 + e ^ {\ alpha + \ beta x}}} $
Gdzie -
Odpowiedź - Obecność / Brak cechy.
Predictor - zmienna liczbowa obserwowana dla każdego przypadku
$ {\ beta = 0 \ Rightarrow} $ P (Obecność) jest taka sama na każdym poziomie x.
$ {\ beta \ gt 0 \ Rightarrow} $ P (Obecność) rośnie wraz ze wzrostem x
$ {\ beta = 0 \ Rightarrow} $ P (Obecność) maleje wraz ze wzrostem x.
Przykład
Problem Statement:
Rozwiąż regresję logistyczną następującego problemu Rizatryptan for Migraine
Odpowiedź - całkowita ulga w bólu po 2 godzinach (tak / nie).
Predyktor - Dawka (mg): Placebo (0), 2,5,5,10
| Dawka | #Patients | #Ulżyło | %Ulżyło |
|---|---|---|---|
| 0 | 67 | 2 | 3.0 |
| 2.5 | 75 | 7 | 9.3 |
| 5 | 130 | 29 | 22.3 |
| 10 | 145 | 40 | 27.6 |
Solution:
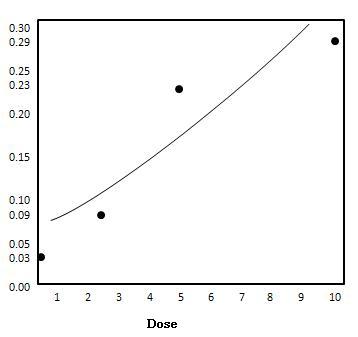
Mając $ {\ alpha = -2.490} i $ {\ beta = .165}, mamy następujące dane:
| Dawka ({x} $) | $ {\ pi (x)} $ |
|---|---|
| 0 | 0,03 |
| 2.5 | 0,09 |
| 5 | 0,23 |
| 10 | 0.29 |