Statystyki - Kurtoza

Stopień ogonowości rozkładu mierzy się kurtoozą. Mówi nam, w jakim stopniu rozkład jest mniej lub bardziej podatny na odstające (cięższy lub słabszy) niż rozkład normalny. Trzy różne typy krzywych, dzięki uprzejmości Investopedia, są pokazane w następujący sposób -

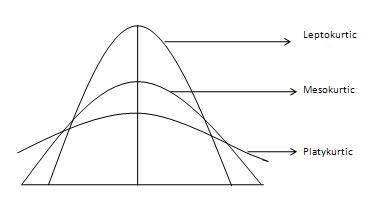
Trudno jest odróżnić różne typy kurtozy na wykresach gęstości (lewy panel), ponieważ ogony są bliskie zeru dla wszystkich rozkładów. Ale różnice w ogonach są łatwe do zauważenia na normalnych wykresach kwantyl-kwantyl (prawy panel).

Krzywa normalna nazywa się krzywą mezokurtyczną. Jeśli krzywa rozkładu jest bardziej podatna na wartości odstające (lub bardziej ogoniona) niż krzywa normalna lub mezokurtyczna, wówczas określa się ją jako krzywą leptokurtyczną. Jeśli krzywa jest mniej podatna na wartości odstające (lub z mniejszymi ogonami) niż krzywa normalna, nazywa się ją krzywą platykurtyczną. Kurtoza jest mierzona momentami i jest określona następującym wzorem -

Formuła

${\beta_2 = \frac{\mu_4}{\mu_2}}$

Gdzie -

${\mu_4 = \frac{\sum(x- \bar x)^4}{N}}$

Im większa wartość \ beta_2, tym bardziej szczytowa lub leptokurtyczna krzywa. Krzywa normalna ma wartość 3, leptokurtyka ma \ beta_2 większe niż 3, a platykurtyczna ma \ beta_2 mniej niż 3.

Przykład

Problem Statement:

Podano dane dotyczące dziennych wynagrodzeń 45 pracowników fabryki. Oblicz \ beta_1 i \ beta_2, używając momentu o średniej. Skomentuj wyniki.

Płace (Rs.)	Liczba pracowników
100-200	1
120-200	2
140-200	6
160-200	20
180-200	11
200-200	3
220-200	2

Solution:

Płace (Rs.)	Liczba pracowników (f)	Środkowy punkt m	m-${\frac{170}{20}}$ re	${fd}$	${fd^2}$	${fd^3}$	${fd^4}$
100-200	1	110	-3	-3	9	-27	81
120-200	2	130	-2	-4	8	-16	32
140-200	6	150	-1	-6	6	-6	6
160-200	20	170	0	0	0	0	0
180-200	11	190	1	11	11	11	11
200-200	3	210	2	6	12	24	48
220-200	2	230	3	6	18	54	162
	${N=45}$			${\sum fd = 10}$	${\sum fd^2 = 64}$	${\sum fd^3 = 40}$	${\sum fd^4 = 330}$

Ponieważ odchylenia zostały wzięte od założonej średniej, dlatego najpierw obliczamy momenty o dowolnym pochodzeniu, a następnie o średniej. Chwile o arbitralnym pochodzeniu '170'

${\mu_1^1= \frac{\sum fd}{N} \times i = \frac{10}{45} \times 20 = 4.44 \\[7pt] \mu_2^1= \frac{\sum fd^2}{N} \times i^2 = \frac{64}{45} \times 20^2 =568.88 \\[7pt] \mu_3^1= \frac{\sum fd^2}{N} \times i^3 = \frac{40}{45} \times 20^3 =7111.11 \\[7pt] \mu_4^1= \frac{\sum fd^4}{N} \times i^4 = \frac{330}{45} \times 20^4 =1173333.33 }$

Chwile wredne

${\mu_2 = \mu'_2 - (\mu'_1 )^2 = 568.88-(4.44)^2 = 549.16 \\[7pt] \mu_3 = \mu'_3 - 3(\mu'_1)(\mu'_2) + 2(\mu'_1)^3 \\[7pt] \, = 7111.11 - (4.44) (568.88)+ 2(4.44)^3 \\[7pt] \, = 7111.11 - 7577.48+175.05 = - 291.32 \\[7pt] \\[7pt] \mu_4= \mu'_4 - 4(\mu'_1)(\mu'_3) + 6 (\mu_1 )^2 (\mu'_2) -3(\mu'_1)^4 \\[7pt] \, = 1173333.33 - 4 (4.44)(7111.11)+6(4.44)^2 (568.88) - 3(4.44)^4 \\[7pt] \, = 1173333.33 - 126293.31+67288.03-1165.87 \\[7pt] \, = 1113162.18 }$

Z wartości ruchu o średniej możemy teraz obliczyć ${\beta_1}$ i ${\beta_2}$:

${\beta_1 = \mu^2_3 = \frac{(-291.32)^2}{(549.16)^3} = 0.00051 \\[7pt] \beta_2 = \frac{\mu_4}{(\mu_2)^2} = \frac{1113162.18}{(546.16)^2} = 3.69 }$

Z powyższych obliczeń można wywnioskować, że ${\beta_1}$, który mierzy skośność jest prawie zerowa, co wskazuje, że rozkład jest prawie symetryczny. ${\beta_2}$ Który mierzy kurtoozę, ma wartość większą niż 3, co oznacza, że rozkład jest leptokurtyczny.