Statystyki - rozkład gamma

Rozkład gamma reprezentuje ciągłe rozkłady prawdopodobieństwa rodziny dwuparametrowej. Rozkłady gamma są opracowywane z ogólnie trzema rodzajami kombinacji parametrów.

Parametr kształtu $ k $ i parametr skali $ \ theta $.
Parametr kształtu $ \ alpha = k $ i parametr odwrotnej skali $ \ beta = \ frac {1} {\ theta} $, nazywany parametrem szybkości.
Parametr kształtu $ k $ i parametr średni $ \ mu = \ frac {k} {\ beta} $.

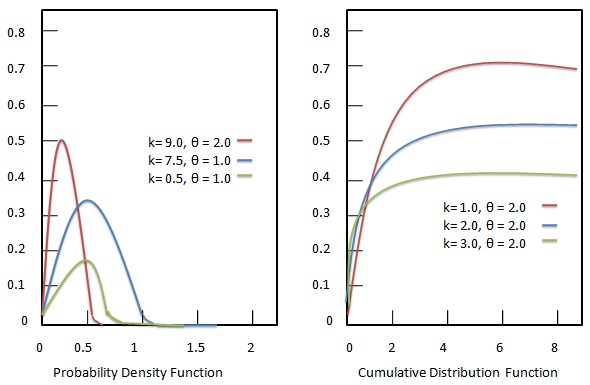
Każdy parametr to dodatnie liczby rzeczywiste. Rozkład gamma to maksymalny rozkład prawdopodobieństwa entropii zależny od następujących kryteriów.

Formuła

$ {E [X] = k \ theta = \ frac {\ alpha} {\ beta} \ gt 0 \ and \ is \ fixed. \\ [7pt] E [ln (X)] = \ psi (k) + ln (\ theta) = \ psi (\ alpha) - ln (\ beta) \ and \ is \ fixed. } $

Gdzie -

$ {X} $ = zmienna losowa.
$ {\ psi} $ = funkcja digamma.

Charakteryzacja za pomocą kształtu $ \ alpha $ i kurs $ \ beta $

Funkcja gęstości prawdopodobieństwa

Funkcja gęstości prawdopodobieństwa rozkładu Gamma jest podana jako:

Formuła

$ {f (x; \ alpha, \ beta) = \ frac {\ beta ^ \ alpha x ^ {\ alpha - 1} e ^ {- x \ beta}} {\ Gamma (\ alpha)} \ gdzie \ x \ ge 0 \ i \ \ alpha, \ beta \ gt 0} $

Gdzie -